О задаче Коши в теории коэффициентных обратных задач для упругих тел

В данной работе мы решаем задачу оценки снизу максимального числа, компонент связности дополнения предельного спектра, ленточных тёплицевых матриц, символы которых, лорановские полиномы заданной степени. Здесь мы уточняем результат, полученный в работе [1], явно указывая параметры символа, последовательности ленточных тёплицевых матриц, дополнение предельного спектра, которых имеет заданное число компонент связности из промежутка, значений, границы которого найдены в работе [1]. Эта. часть общей задачи исследования геометрии предельного спектра. Следует сказать, что знание геометрии предельного спектра, может быть полезно как при аналитическом исследовании асимптотического поведения собственных значений ленточных тёплицевых матриц, поскольку дифференциально-геометрические свойства, предельного спектра, связаны со скоростью сходимости собственных значений к точкам предельного спектра, так и при приближенном нахождении собственных значений, поскольку позволяет уточнить области выбора, начальных приближений [2]. Кроме того, геометрия и топология предельного спектра, может отражать важные качественные характеристики физических моделей, исследование которых сводится к исследованию предельного спектра, тёплицевых матриц (правда, как правило, не ленточных). Данная работа, также, как и работа. [3], содержит результаты, уточняющие топологические характеристики предельного спектра.

Уточним постановку задачи. Сначала, напомним необходимые для понимания работы понятия (см. [3]). Пусть f — комплекснозначная функция, аналитическая в окрестности окружности единичного радиуса S ¹ = {z G C : |z| = 1}:

f (z) = X akzk •                              W k∈Z

Будем обозначать через Tn(f ) тёплипеву матpuny размера n х n. т. е. матрицу Tn(f ) = (aij )Пд=м матричные элементы которой задаются формулой aij = ai-j, г де ak находятся

из (1). Отметим, что у тёплицевой матрицы на каждой из диагоналей, параллельных главной, стоят одинаковые элементы. Заметим, что если для k < —r и для k > h, ak = 0, т. е. аналитическая функция f (z) превращается в лорановский полином h f(z) = X akzk, k=-r то соответствующая такой функции тёплицева матрица называется ленточной.

Упорядочим каким-нибудь образом собственные значения {A_n,_i}n₌-_n+1 матрицы Tn(f ), например, по возрастанию их модуля: |A_n,i| 6 |A_n,j| при i <  j. Пусть an = a(T_n (f )) = {A_n,o,..., A_n,_n} — спектр матрицы Tn(f ). Множество предельных точек последовательностей {Ak}, г де Ak G aik, limk^^ ik = то будем называть пределиним спектром последователъности тёплицевых матриц {Tn(f )}П=1 и обозначать через ai(f).

Естественные вопросы, которые сразу возникают: как связан предельный спектр с функцией f (z) (которую также называют символом каждой из матриц последовательности {Tn(f )}П=₁), какова геометрическая структура предельного спектра? Естественно ожидать, что ответ на второй вопрос будет дан в терминах функции f.

Задача геометрического описания предельного спектра издавна привлекает внимание многих математиков. В классической работе Ф. Спитцера и П. Шмидта [4] было получено описание предельного спектра в терминах совпадения модулей корней многочлена строящегося по символу последовательности ленточных тёплицевых матриц. Используя такое описание Ф. Спитцер и П. Шмидт доказали, что предельный спектр, либо одномерное множество, являющееся объединением аналитических дуг, либо нульмерное множество. Позднее Ульман доказал связность предельного спектра [5]. Более тонкие геометрические вопросы о строении предельного спектра ленточных несамосопряженных матриц являются нерешенными до настоящего времени. В данной работе мы исследуем вопрос о числе компонент дополнения предельного спектра ленточных тёплицевых матриц. Нетривиальным уже является тот факт, что число этих компонент может быть сколь угодно большим, оно растет не медленнее некоторой линейной функции от степени многочлена f — символа ленточной тёплицевой матрицы. Мы строим конкретные примеры символов — полиномов Лорана, таких, что предельный спектр соответствующих им тёплицевых матриц разбивает комплексную плоскость на максимальное число компонент связности равное [ k-y¹], г де 2k — степень полинома Лорана, являющегося символом данной последовательности тёплицевых матриц. Как отмечено выше, мы уточняем в данной работе, результат полученный в работе [1], явно строя такие символы, что предельный спектр тёплицевых матриц, определяемых этими символами, разбивает комплексную плоскость на любое наперед заданное число компонент связности из промежутка {1, 2,..., [щщ]}- Точнее говоря. мы показываем явными формулами, каким образом следует выбирать параметры полиномов Лорана для того, чтобы предельный спектр разбивал комплексную плоскость на заданное число компонент связности г, где 1 6 r 6 [ ky¹ ]• В приложении приведены численные примеры, подтверждающие справедливость полученных результатов. Таким образом, мы получаем некоторые оценки снизу для максимального числа компонент на которые может разбивать комплексную плоскость предельный спектр последовательности тёплицевых матриц с символом заданной степени k. Ниже мы будем использовать следующие стандартные обозначения. Через a(A) будем обозначать спектр оператора, A;

a(A) = {A G C : A — AI — newЗратим}.

• 2.    Основной результат работы

Будем рассматривать многочлен

b(t) = р + t-k(t - a)k(t - в)к,(2)

где р, а, в — комплексные числа и a • в = 0. Пусть

a(t) = t-1(t — a)(t — в)-(3)

Легко видеть, что в силу формул (2), (3)

b(t)= р + (a(t))k.(4)

Следующая лемма приведена в работе [1].

Лемма 1. Предельные спектры последовательностей ленточных тёплицевых матриц с символами a(t) и b(t) связаны следующим соотношением:

ai(b(t)) = Р + (ai (a(t))')k -(Д

Сформулируем теперь основной результат работы. Пусть k — натуральное число, а b(t) определяется формулой (2). Тогда имеет место следующая теорема.

Теорема 1. 1- Если k = 1 a.тп k = 2. то C \ ai (b) связен.

• 2.    Если k >  3, то C \ ai(b) может иметь [k+y¹] компонент (включая неограниченную компоненту).

• 3-    Для каждого натурального числа j moi кду 1 и [k+y¹] существлтот такие а. в- ^что C \ ai (b) имеет ровно j компонент. Именно а. в находятся из уравнений:

( ^{— (а + в) + 2}V^a •^в = fl, ( ^{— (a + в) — 2}V^a • ^в = ^f2-

При этом f1, f2 следует выбирать так, чтобы разность значений их аргументов удовлетворяла следующему условию:

^{n (} r - 1) < | arg(fi) — arg(f2)| < ^ПГ, r = 1,---,k-                   (7)

В этом случае число компонент связности дополнения предельного спектра, будет равняться [ry-] .

<1 Так как дополнение отрезка прямой связно, то мы получаем из равенства (5) доказываемое утверждения для k = 1. При k = 2 мы получаем, что предельный спектр ai(b) представляет собой простую разомкнутую кривую, поскольку угол между концевыми точками в этом случае больше чем п и меньше, чем 2п. В этом случае также получается одна компонента связности дополнения предельного спектра. Покажем, что в силу формулы (5) и учитывая, что ai(a) это отрезок, множество ai (b) имеет не более [ky-¹] компонент и что каждое значение числа компонент между 1 и [ky¹] может быть реализовано (например, мы получаем точно [Д-Д], если значение |р — (а + в)| > 0 достаточно мало II значение |а • в| > 0 достаточно велико). Допетвнтелыю. выберем (рокуеы f1. f₂ так, чтобы выполнялось условие (7), т. е.

^{n (} sk 1) < ^{1 ar}g^(fi) ^{— ar}g^(f2^)|< ^ks, s = ¹,---,k-                   (8)

Именно, пусть f1 = r • exp ( ⁿ i ( Sk 1) ), f ₂ = r • exp (— ⁿ i ( Sk 1) ). Тогда, используя формулу (6), мы находим явные значения параметров а, в^:

( ^а = ^- f+f² + 2 Vf1 • ^f2, 1^e = ^{— f1}t f^{2 —} 2 vfi • ^f2 •

Нетрудно видеть, что предельный спектр ai(а) представляет собой отрезок: ai(а) = {z G C : z = z(t) = tf1 + (1 — t)f₂, 0 6 t 6 1}. Будем следить за точками отрезка при возведении в k-ую степень (мы отождествляем точки плоскости с комплексными числами):

^(z(t))k = ^(tfi ^{+ (1—}t^^k = (t • (г • exp ( ⁿi ⁽ s , \ \        \    2k

+ (1 — t )

r • exp

-

ni(s — 2k

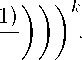
Будем следить сначала за концевыми точками отрезка z(1), z(0). Получаем:

(z(1))k = (fi)k = rk • exp

ni(s — 1) 2

(z(0))^k = (f)^k = rk • exp

ni(s — 1) 2

Нетрудно видеть, что в силу непрерывности отображения возведения в степень, образом отрезка при этом отображении является кривая, имеющая [s^-1] самопересечений. (При возведении в степень модуль и аргумент функции являются непрерывными функциями, соответственно, модуля и аргумента независимой переменной.) В силу монотонности роста (убывания) модуля точек отрезка z при возведении в степень k пр и |z| > 1 (|z| < 1) все точки самопересечений различны. Следовательно, эта кривая разбивает плоскость на [s^-1] + 1 = [s^-¹] компонент связиости при s = 1,• • •, k. B

ЗАМЕЧАНИЕ 1. Отметим, что из доказательства теоремы следует явный способ построения символа тёплицевых матриц, предельный спектр которых делит комплексную плоскость на число s = 1,..., k компонент связности, удовлетворяющих условию теоремы. Действительно, зафиксируем произвольное комплексное число zg, отличное от 0. Выберем угол ф, удовлетворяющий условию (8):

As—) <ф<тг.

kk

Положим f1 = zg, f₂ = e^iфzg. Используя формулы (9) найдем явно значения параметров а. в^:

(а = — z ^{o + e}^^z 0 + 2 z_ge^/²,

( в = — ^z o +^^z o — 2 zg ei№.

• 3.    Приложение. Примеры вычисления предельных спектров

Рассмотрим символ b(t) = ц + t^-k(t — a)^k (t — в )^k с парат гетрами ц = 0 + i. а = 3 — 5i. в = 1 + 3i. Ниже приведены примеры построения предельного спектра последовательности тёплицевых матриц с символом b(t). На рис. 1, 3 приведены графики предельных спектров, построение которых осуществлено на основе доказанной выше теоремы 1, на рис. 1 для параметра k = 1. а па рис. 3 для 31 кгчения параметра, k = 3. На рис. 2. 4

приведены примеры построения спектров тёплицевых матриц размера 20 х 20 с символом b(t), выполненных с использованием программы аналитических вычислений Maple. Видно, что уже для матриц размера 20 х 20 предельный спектр достаточно хорошо приближается обычным спектром.

Ниже приведены графики предельного спектра (рис. 1) и спектра тёплицевой матрицы размера. 20 х 20 с сим волом b(t) = ц + t-k(t — a)k (t — в)^к Щш k = 1. В этом случае дополнение предельного спектра, связно (число компонент связности равно 1).

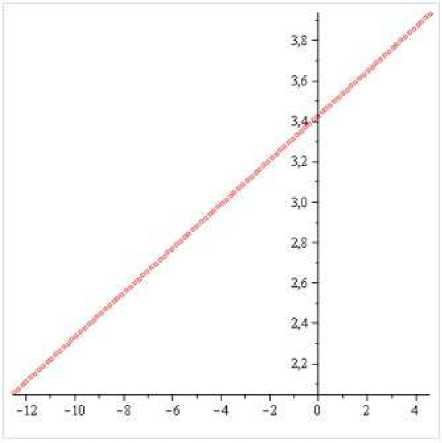
Рис. 1. Предельный спектр тёплицевой матрицы с символом b(t) при k = 1.

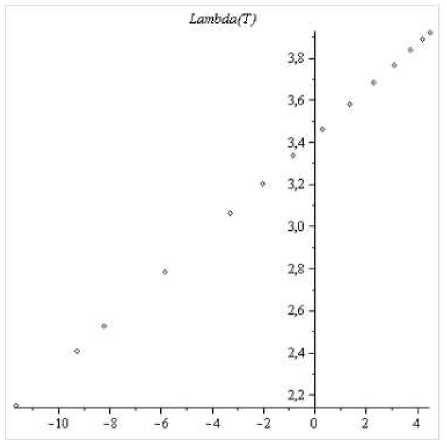
Рис. 2. Предельный спектр тёплицевой матрицы размера 20 х 20 с сим волом b(t) при k = 1 (Maple).

Заметим, что далее мы используем формулу (8). В этом случае s = k = 3, arg(f1) — arg(f₂) = 2.48, и это значение удовлетворяет условию

— < 2.48 < п.

В этом случае достигается максимальное число компонент связности предельного спектра, равное 2.

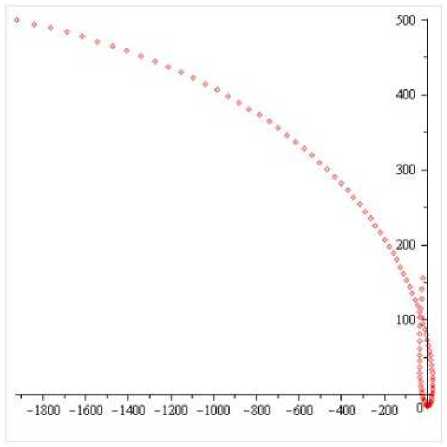
Рис. 3. Предельный спектр тёплицевой матрицы с символом b(t) при k = 3.

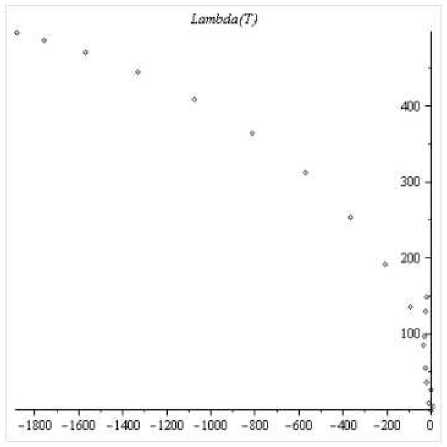
Рис. 4. Предельный спектр тёплицевой матрицы размера 20 х 20 с сим волом b(t) щ m k = 3 (Maple).

Следующий рисунок содержит график предельного спектра, символа

b(t) = д + t-k(t - a)k(t - в)k с параметрами ^ = 1 + 3.9i, а = 2 + 7i, в = —1 — 3i, k = 6, разбивающего комплексную плоскость на. 3 компоненты связности.

1J х 10е-

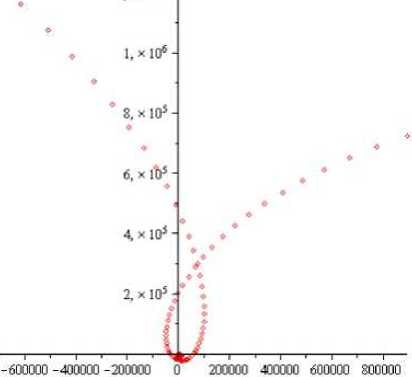
Рис. 5. Предельный спектр тёплицевой матрицы с символом b(t) при k = 6.