О задаче организации ходьбы экзоскелетона нижних конечностей при помощи управления в коленных шарнирах
Автор: Лавровский Э.К., Письменная Е.В., Комаров П.А.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (68) т.19, 2015 года.
Бесплатный доступ
Рассматриваются проблемы организации ходьбы активного экзоскелетона в режиме плоской регулярной ходьбы по ровной горизонтальной поверхности. Предполагается, что экзоскелетон снабжен двумя двигателями в коленных шарнирах, а взаимодействие с человеком осуществляется при помощи вязкоупругих лямок, соединяющих его и аппарат в некоторых точках тела. Рассматриваются два типа управляющих двигателей - идеальные моментные и гидравлические двигатели. На аппарате, кроме того, установлены датчики межзвенных углов и угловых скоростей. В работе построена система динамических уравнений, описывающих движение экзоскелетона в режиме одноопорной ходьбы при воздействии вязкоупругих сил за счет лямок и управляющих моментов. Режим ходьбы задается человеком-оператором, который поддерживает его за счет собственных мышечных усилий; информация об углах считывается датчиками, установленными в суставах. На основе полных уравнений динамики строится управление экзоскелетоном, обеспечивающее отслеживание желаемых движений в коленных шарнирах с требуемым качеством переходных процессов. В случае идеальных двигателей моделирование показало правильность построенных алгоритмов и высокую точность реализации задаваемой походки (в том числе и по угловому положению корпуса экзоскелетона), а также выявило существенное влияние коэффициентов демпфирования и упругости лямок. Исследование показало возможность подбора коэффициентов, позволяющих обеспечить комфортность движения для человека-оператора за счет резкого снижения вибраций в системе. Одновременно с этим наблюдается снижение энергозатрат человека, подсчитанных по критерию биомеханического функционала. Описана модель экзоскелетона, учитывающая динамические свойства гидроцилиндров и геометрию их расположения; они также устанавливаются в коленных шарнирах. Построено управление, которое позволяет одновременно реализовать с требуемым качеством как желаемые угловые перемещения в коленных шарнирах, так и необходимые усилия, развиваемые в гидроприводах. При моделировании была установлена существенная роль коэффициента усиления в алгоритме для обеспечения устойчивости вычислительного процесса.
Экзоскелетон, точки контакта тела и аппарата, отслеживание желаемого момента сил в коленях
Короткий адрес: https://sciup.org/146216171
IDR: 146216171 | УДК: 521.1,
Текст научной статьи О задаче организации ходьбы экзоскелетона нижних конечностей при помощи управления в коленных шарнирах
Рассматривается плоская одноопорная регулярная ходьба экзоскелетона, надетого на человека, по ровной горизонтальной поверхности – как с грузом, так и без
Лавровский Эдуард Кирович, ведущий научный сотрудник, лаб. № 301 НИИ механики МГУ, Москва
Письменная Елена Валентиновна, старший научный сотрудник, лаб. № 301 НИИ механики МГУ, Москва
Комаров Павел Алексеевич, научный сотрудник, лаб. № 301 НИИ механики МГУ, Москва него. Механизмы подобного типа призваны помочь как здоровому человеку при перемещении тяжелых грузов или при длительной ходьбе, так и людям с ограниченными двигательными возможностями.
Экзоскелетон расположен частично за спиной и по бокам тела человека, в его «рюкзаке» может находиться дополнительный точечный груз. Тело человека и конструкция экзоскелетона, хотя она и повторяет человеческое тело, не слиты вместе: контакт поддерживается лишь в восьми точках тела при помощи упругих лямок, которые рассматриваются как упругие линейные пружинки с различными коэффициентами упругости и демпфирования. Этими восьмью точками являются плечи человека, условная середина его корпуса и таз, а также середины бедер и голеней каждой из ног; еще одной точкой контакта является точка стопы (голеностопный сустав) переносимой ноги. Считается, что стопы опорных ног человека и аппарата совпадают во все время одного рассматриваемого шага. Таким образом, экзоскелетон может в некотором смысле повторять диктуемое ему человеком движение. Если конструкция экзоскелетона «наползает» на человеческое тело, то считается, что это вызывает резкий рост коэффициентов упругости пружинок в соответствующих точках контакта, стремящихся вытолкнуть «железо» из тела.
Задачей организации ходьбы аппарата является осуществление движения стопы переносимой ноги, таза и корпуса по заданным желаемым траекториям. Особенностью работы является использование только двух управляющих приводов в коленях обеих ног, помимо этого на аппарат воздействуют упругие силы со стороны крепежных лямок.
В работе рассматриваются два типа режимов управления: в случае «идеального» привода и гидропривода.
Динамика аппарата
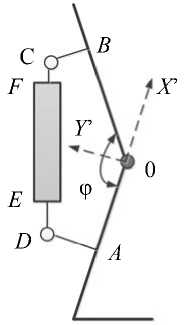
Рассматривается задача управления биомеханизмом – человеком, интегрированным с экзоскелетом, при перемещении его по ровной горизонтальной поверхности в режиме плоской регулярной одноопорной ходьбы. Человек может иметь различный рисунок ходьбы, а экзоскелетон должен его воспроизвести за счет наличия лямок, осуществляющих пассивную связь с человеком, но при этом дающих ему некоторую свободу перемещения, и двигателей. Для управления экзоскелетоном необходимо получать данные об углах и угловых скоростях в суставах человека на каждом такте управления. Они могут быть, например, измерены, как описано в [5]. На рис. 1 показана схема аппарата в абсолютной системе осей XYZ , введены обозначения углов, моментов M i , j ( i = 1,2; j = 1,2,3) в шарнирах; в стопах ног – в точке ( x 1 p , y 1 p ) опорной ноги приложены силы реакции R 1 x , R 1 y , в стопе переносимой ноги ( x 2 p , y 2 p ) силы реакции, естественно, отсутствуют. Равен нулю также стопный момент в переносимой ноге M 21 . Определяющими координатами тела человека являются ( x ∗ , y ∗ ) – координаты тазобедренного сустава, а также углы звеньев тела с вертикалью ( ψ∗ , α 1 ∗ , β 1 ∗ , α∗ 2 , β∗ 2 ) . Положение «тела» экзоскелетона описывается одноименными координатами ( x , y , ψ , α 1, β 1, α 2, β 2), причем всюду далее считается, что эти координаты относятся именно к экзоскелетону.
Пусть, например, человек-оператор, используя собственные мышечные усилия, движется строго в режиме комфортабельной ходьбы [1]
x * = Vt -g , y * = h , V = L / T , a = L /2, x p = y p = 0, (1)
где V – скорость его движения; T – период одного шага; h – высота подъема точки таза над горизонтальной поверхностью; L – длина шага (все эти величины постоянны), причем перемещение его переносной ноги подчиняется закону x2p =-Lcos(Qt), y2p = 5'sin'(Qt), Q = n/ T,
где 5 - некоторая константа, задающая высоту траектории переносимой ноги (обычно 5 2 = 0,02 м), и, наконец, угол корпуса у * [1] изменяется по периодическому закону
У * ( t )
ML
2 K r
ch to t
1 + ch to T ----------sh to t
Mx *
K r ,
L
G = 2’
to 2
Krg
J + K r h
Здесь M , Kr , J – масс-инерционные характеристики человеческого тела, смысл которых будет пояснен ниже; g – ускорение силы тяжести. Экзоскелетон только отчасти повторяет такое («желаемое») движение, причем на его истинное движение влияют силы, развиваемые лямками в точках контакта, а также управляющие моменты, сосредоточенные в коленных шарнирах.
Используя метод Лагранжа, можем получить в общем случае следующую систему [1], описывающую движение экзоскелетона, структурные уравнения которой имеют вид
B ( z ) |И|+ D ( z ) | z 211 + Ag ||sin z || = Q z ,
где || z || = || x , y , у , a 1 , P 1 , a 2 , P 2|| - вектор пространства переменных, а B ( z ), D ( z ), A -некоторые матрицы. Вид этих уравнений аналогичен приведенным, например, в [4].
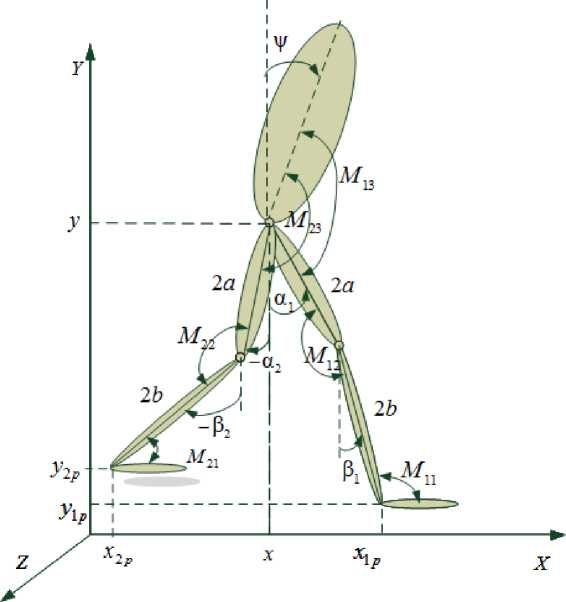
Рис. 1. Схема экзоскелетона в движении
Здесь обозначено Q z = | Q x , , Q y , Q „ , Q „ 1 , Q , Q „ 2 , Q e | T , где
Q x = R x + Q X , R 2 x = 0,
Q y = R y + Q y , R 2 y = 0,
Q , =- £ M » + q ; •
i = 1
Q a = — Mi 2 — Mi 3 + 2 a ( R ix cos a i + Riy sin a i ) + Q L , i = 1,2 Q, = Mn + 2 b ( R x cos P i + R y sin P i ) + Mn + Q ^ , i = 1, 2,
M = m t + 2 m a + 2 mb , J * = Ja + 4 mba 2, Ka = m a a . + 2 mba , K b = mA , J ab = 2 m b ab . , K r = m t r .
В соотношениях (4)-(6) используются следующие обозначения: Q * с различными нижними индексами – обобщенные силы и моменты за счет лямок; R ix , R iy – силы реакций опоры; 2 a и 2 b соответственно длины бедер и голеней экзоскелетона (и человека); ma , mb – их массы; mt – масса корпуса; r – расстояние центра масс корпуса от таза; a . , b . - соответственно расстояния центров масс бедра и голени от таза и коленей ног; J ab и Ja – моменты инерции соответственно корпуса и бедра относительно точки таза; Jb – момент инерции голени относительно колена.
Уравнения (4), (5) в принципе пригодны для описания движения как в одноопорной (с мгновенной двухопорной фазой), так и с протяженной двухопорной фазой, а также в режиме с протяженной двухопорной фазой, где сочетаются обе фазы. Под номером один понимается передняя опорная, под номером два – задняя переносимая нога. Стопы человека и экзоскелетона считаются невесомыми. Поскольку далее рассматривается одноопорная ходьба, количество введенных переменных переопределено, так как координаты таза могут быть выражены через углы опорной ноги, что позволяет получить систему [6] с меньшим числом независимых переменных. Система масс-инерциальных характеристик тела человека и экзоскелетона, используемых ниже во всех численных экспериментах, указана в Приложении. Экзоскелетон может быть нагружен дополнительно грузом массой порядка P = 50–100 кг на корпусе, на высоте rol = 45 см от таза. Лямки считаются невесомыми.
Заметим, что (в отличие от [1, 2, 4, 6]) данная динамическая система содержит в правых частях формул (5) функции Q * , которые отражают воздействие пружин (лямок) в точках контакта с телом человека. Они играют важную роль в управлении движением экзоскелетона. Эти Q * представляют собой обобщенные силы, связанные с воздействием сил F вязкопругих пружин в точках крепления по соответствующим координатам лагранжевых уравнений,
Fx = С A x + d ^ 5c , Fy = С A y + d A y , (7) где С – коэффициент жесткости, H∙см–1; d – коэффициент демпфирования, H∙c∙см–1; а A x , A y - рассогласования по осям x , y координат точек крепления на теле оператора и на аппарате. Расположение восьми точек крепления показано на рис. 2.
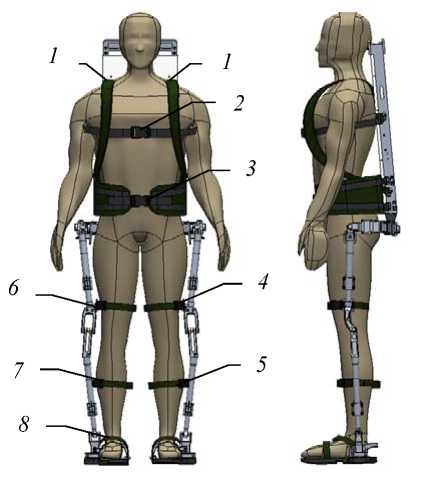
Рис. 2. Человек-оператор в экзоскелетоне
Рама аппарата в отличие от корпуса человека, который моделировался равномерно распределенным прямолинейным стержнем, рассматривалась как имеющая перевернутую Г-образную форму с горизонтальным (невесомым) участком смещения displ = 10 см, которым она прикреплялась к тазу аппарата. Приведем вид всех функций Q * :
88 q- Z f x - q ; = Z f ; • i = 1 i = 1
Q V = - rop ( F x cos V + Fxy sin v ) — rog ( F x cos v + F , sin v ) + disp (sin V Z F-cos v Z Fyi ],
Q ; = l 4 ( F x cos a , + F , sin a , ) + 2 a ( F x cos a , + F , 5 sin a , ), Q" = 1 , ( F x cos ₽ , + F , 5 sin ₽ , ), Q a 2 = l 4 ( F x cos a 2 + F 6 sin a 2 ) + 2 a ( F X cos a 2 + F 7 sin a 2 ), Q 2 = l 5 ( F X cos P 2 + F 7 sin в 2 ) + + 2 b ( F x 8cos p 2 + Fy 8sin P 2 ).
Верхние индексы в написании сил F отвечают номерам точек крепления. При численных экспериментах было принято, что rop = 60 см (высота точки 1 от таза), rog = 20 см (высота точки 2 от таза), l 4 = 1 6 = 35 см (расстояние точек 4 и 6 от таза), l 5 = 1 7 = 30 см (расстояние точек 5 и 7 от коленного сустава). Масс-инерционные характеристики тела человека брались для нижних конечностей согласно [3] (они приводятся в Приложении). Массы рамы, обоих бедер и голеней аппарата принимались равными 5 кг при равномерном распределении массы. В случае управления движением экзоскелетона при помощи гидроцилиндров массы каждого из бедер и голеней увеличивались еще на 2,5 кг. Принятые параметры комфортабельного движения человека-оператора и некоторые другие динамические параметры приводятся ниже:
L = 50 см; h = 84,5 см; T = 0,7 c; 2 a = 51,4 см; 2 b = 40,2 см; C = 250 H/см; kd = 0 , 1 c; M = 89,1 см; mtm = 47,6 см; m e = 5 см; r = 37,05 см; rol = 45 см; P = 50-100 кг;
Kr = rmtm + Prol + mte ( r 2 + displ 2), J = ( mtm + mte ) r 2/3 + P ( rol 2 + displ 2).
Здесь mte и mtm – массы корпусов экзоскелетона и человека; C – жесткости лямок на корпусе; d – коэффициент демпфирования, d = C ⋅ kd (где kd – некоторые значения), причем принималось, что жесткости и соответствующие коэффициенты демпфирования на ногах в 12,5 меньше. Приведенные выше величины M , Kr , J использовались в соотношениях формулы (3).
Построение законов управления движением экзоскелета с идеальным ДВИГАТЕЛЕМ В КОЛЕННЫХ ШАРНИРАХ . Р ЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ИССЛЕДОВАНИЙ АЛГОРИТМА
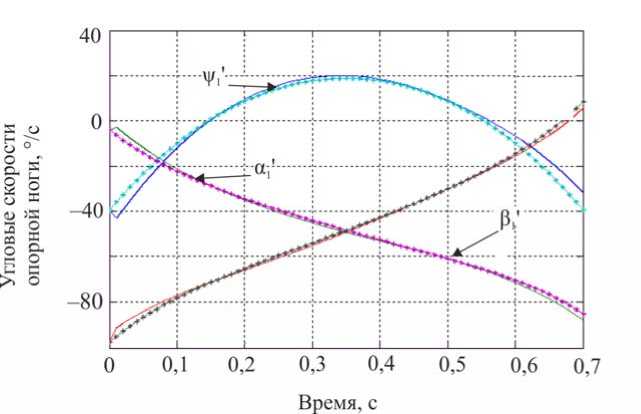
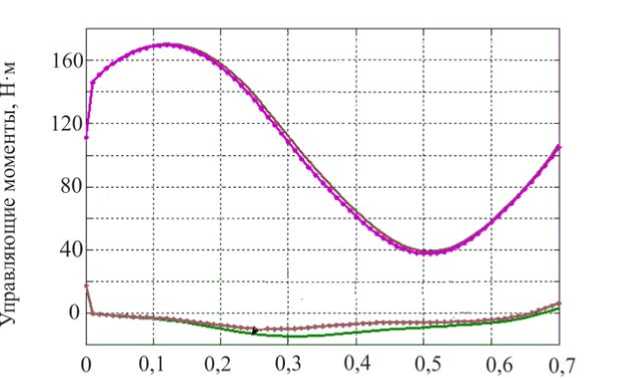
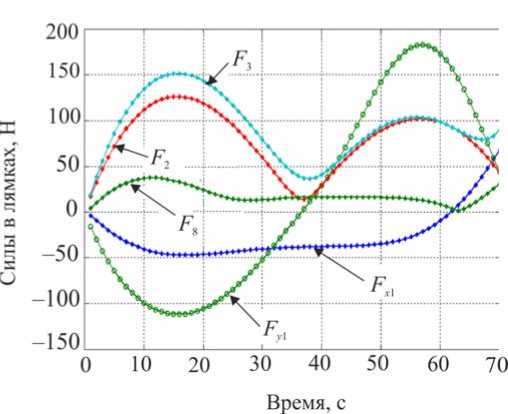
Объектом исследования данного раздела является управляемый экзоскелетон с идеальными двигателями, расположенными в коленных шарнирах, который связан с человеком еще и посредством упруговязкой системы лямок. Остальные управляющие моменты в бедренных и голеностопных шарнирах Mi 1 = Mi 3 ≡ 0, i = 1,2.
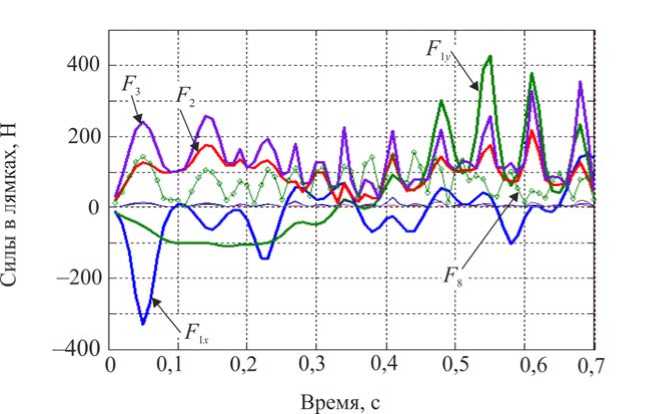
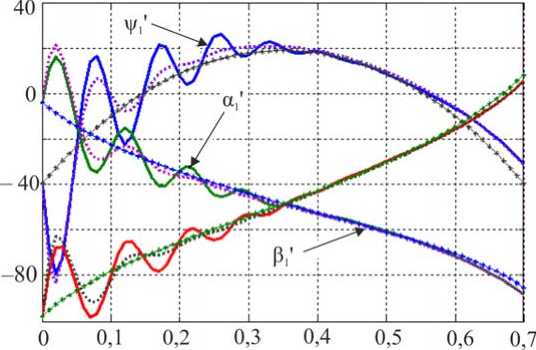
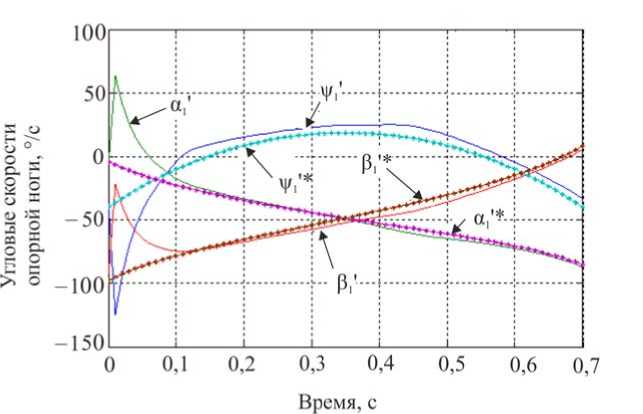
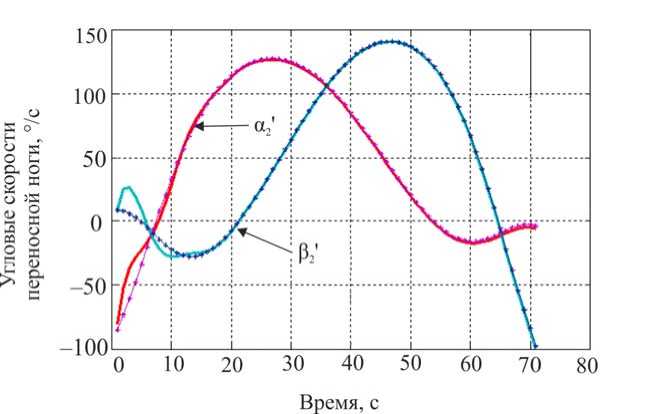
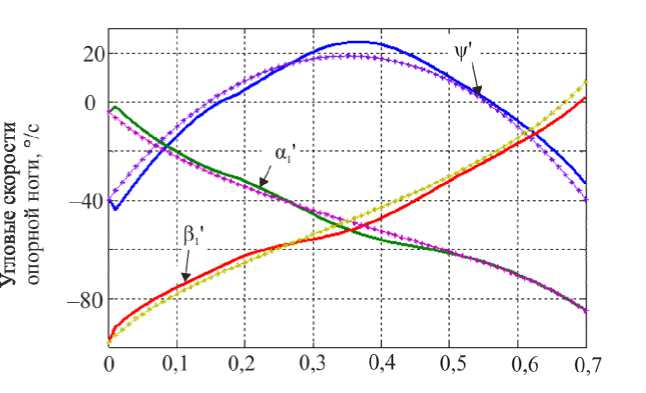
Как указывалось выше, предполагается, что при синтезе доступной является информация обо всех межзвенных углах и их скоростях. Построим алгоритм управления коленным шарниром экзоскелетона, обеспечивающий желаемое движение в виде
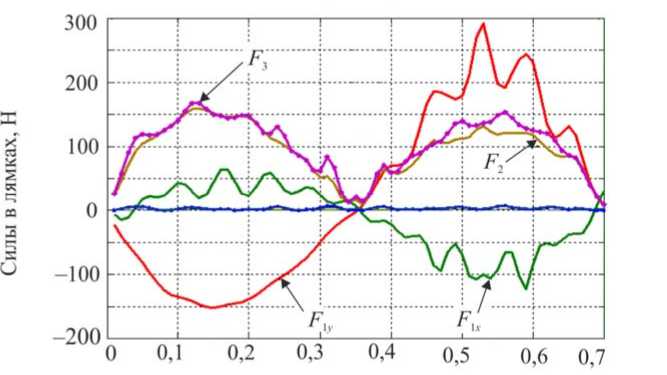
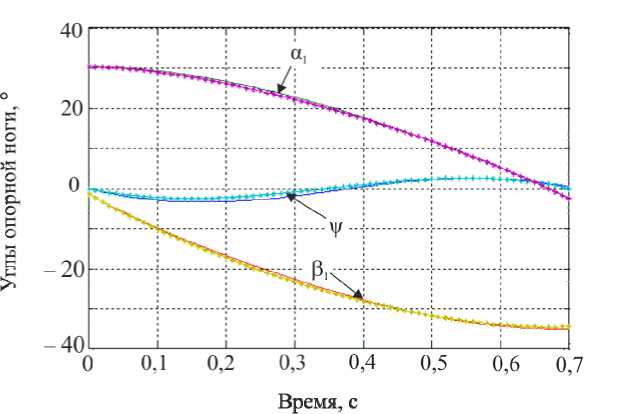
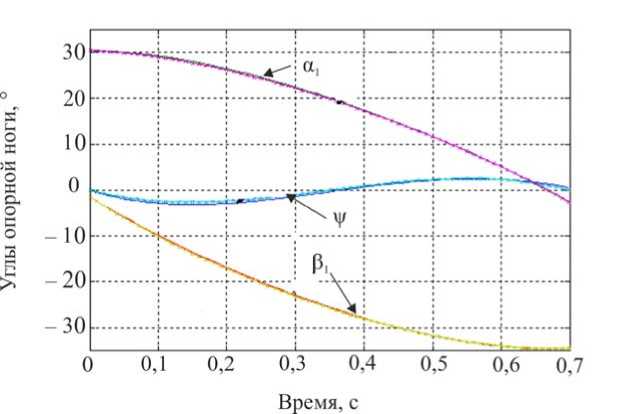
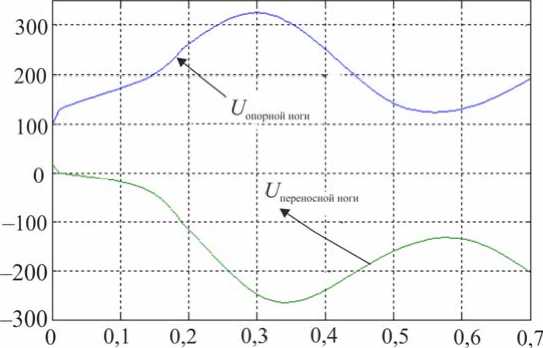
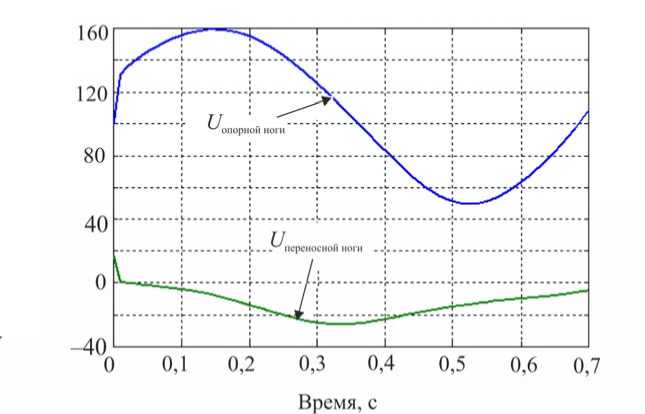
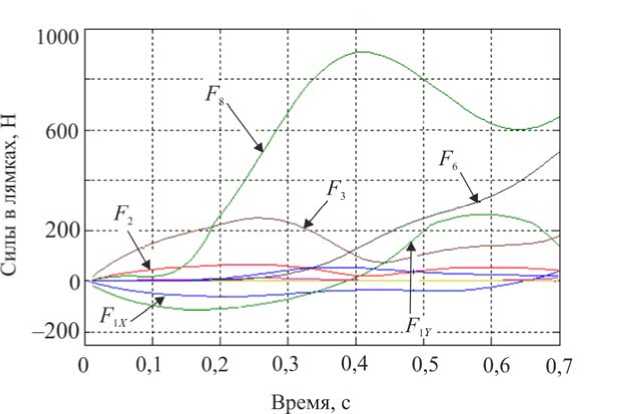
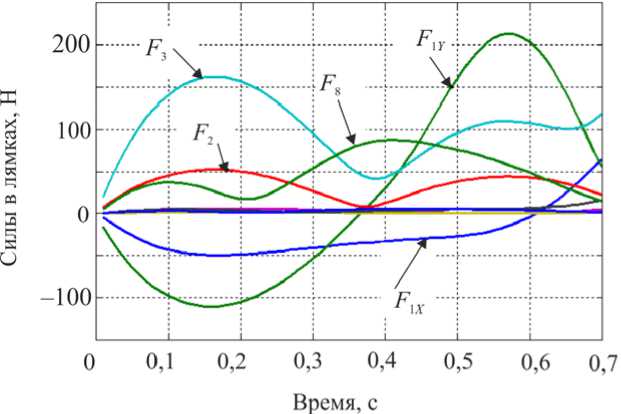
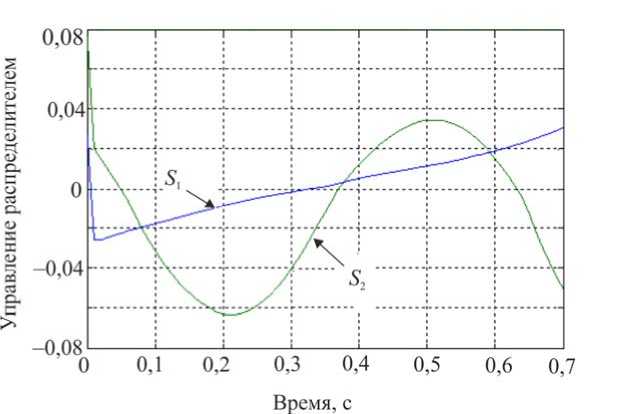
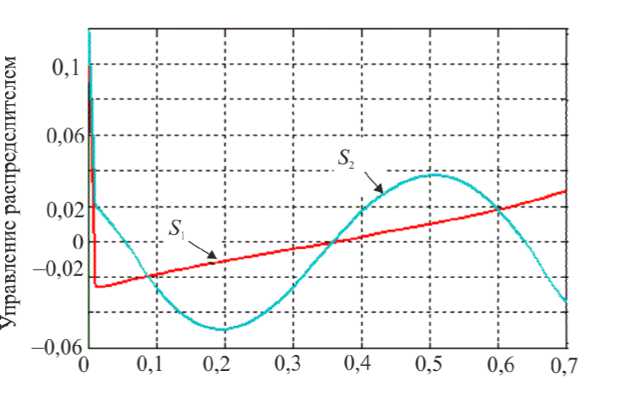
ф, = X( где ϕi – межзвенный угол в i-м (i = 1,2 ) коленном шарнире, ϕi=π-αi+βi; λ, µ – неположительные константы, являющиеся настроечными параметрами системы управления. Величины желаемых углов, скоростей и ускорений ф*, ф*, ф* определяются формулами комфортабельной ходьбы человека (1)–(3). Управляющей функцией является желаемый коленный момент, который затем можно реализовать каким-либо двигателем – электромеханическим, пневматическим или гидродвигателем. Двигатель считается идеальным, если он развивает требуемый момент. Для определения управляющего коленного момента рассматривалась система, состоящая из динамических уравнений (4), (5), условия (8) и дважды продифференцированных кинематических условий в углах, характеризующих неподвижность пятки опорной ноги на подстилающей поверхности. Вся эта система может быть структурно представлена в виде А1(z, Z)||z|| + А2(z)|М = E(z, Z) , где zT =x,y,ψ,α1,β1,α2,β2, wT = R1x,R1y,M12,M22 и A1, A2, E – некоторые матрицы, зависящие от z, z. Такое представление позволяет, решая на каждом шаге интегрирования линейное алгебраическое уравнение (9), определить вторые производные по линейным и угловым переменным ||z||, а также величины R1x,R1y,M12,M22 . Две последние являются искомыми управляющими функциями U=M, U=M. опорной ноги 12 , переносной ноги 22 . Построенный алгоритм исследовался методом математического моделирования на электронно-вычислительной машине. Задавались различные варианты нагрузок на экзоскелетон: 0; 50 и 100 кг. Выбор параметров управления исследовался в широком диапазоне значений коэффициентов λ,µ . например, при следующих наборах λ, µ: µ=-7 с-2,λ=-10с-1, µ=-1 с-2,λ=-0,5с-1, Приемлемые результаты были получены, µ=-2с-2,λ=-10с-1, µ=-12с-2,λ=-35с-1. Ниже на рис. 3–5 приведены графики управляющих моментов в коленях экзоскелета и сил в лямках, возникающих, когда масса груза P составляет 0 или 50 кг для параметров управления λ=-10 с-1,µ=-2с-2и в отсутствие демпфирования в лямках. Нижние индексы в написании величин F отвечают номерам точек крепления и компонентам этих сил по осям x, y. Из графиков видно, что груз способствует развитию колебаний в системе. Это видно также и из графиков угловых скоростей опорной ноги (рис. 6), хотя сами углы отрабатываются неплохо – особенно при P = 0 кг. Сходные по характеру графики были получены и при остальных наборах λ, µ, тем самым при отсутствии демпфирования один коленный привод не способен создать процессы без колебаний по всем переменным, характеризующим движение экзоскелета. Время, с Рис. 3. Графики управляющих моментов при α = -10; µ=-2 . Синяя линия – U переносной ноги; зеленая линия – U опорной ноги при P = 50; черная пунктирная линия – U переносной ноги; розовая пунктирная линия – Uопорной ногипри P = 0 Время, с Рис. 4. Графики сил, возникающих в крепежных лямках экзоскелета при P = 0; λ = -10; µ=-2 Рис. 5. Графики сил, возникающих в крепежных лямках экзоскелета при P = 50; X = -10; ц = -2 Время, с Рис. 6. Графики угловых скоростей опорной ноги экзоскелета при P = 50; X = -5; ц = -7 Используем в креплении лямок демпферы и изучим получающиеся процессы. Тенденция успокоения процесса хорошо видна на графиках угловых скоростей в опорной ноге, построенных при нагрузке P = 50 кг и при значениях kd = 0,01 с-1 (сплошные линии) и kd = 0,025 с-1 (пунктир); звездочками здесь и ниже маркируется желаемый режим. Однако, пожалуй, наилучшие результаты были получены при kd = 0,1 с-1 на рис. 7-11, где при различных параметрах X, ц показано поведение угловых скоростей и силовых переменных процесса. Рис. 7, 8 относятся к случаю X = -12 с-1, ц = -35 с-2. Из этих графиков видно, что большие значения настроечных параметров управления приводят к резкой реакции системы на всякого рода рассогласования, например, начальные. В работе исследовался и другой вариант модели, при которой точность отработки желаемых траекторий заметно повышается. Он заключался в ограничении роста коэффициента жесткости при «проникновении» лямок в тело оператора. Было принято, что увеличение коэффициента C не превышает первоначальную величину в два раза, т.е. Clim = 2C, что больше отвечает конструкции человеческого тела, состоящего из мягких и твердых тканей. Результаты для такой модели приведены на рис. 9–11. Рис. 7. Графики угловых скоростей опорной ноги экзоскелета при P = 50; kd = 0,1; X = -12; ц = -35 Рис. 8. Графики угловых скоростей переносной ноги экзоскелета при P = 50; kd = 0,1; X = -12; ц = -35 Рис. 9. Графики угловых скоростей опорной ноги экзоскелета при P = 50; kd = 0,1; X = -5; ц = -7 Время, с Рис. 10. Графики управляющих моментов при α = -10; µ=-2 . Красная линия – U опорной ноги, зеленая линия – U переносной ноги при λ = -10; µ=-2, -7 ; фиолетовая пунктирная линия – U опорной ноги, коричневая пунктирная линия – U переносной ноги при λ = -12; µ=-35 Рис. 11. Графики сил, возникающих в крепежных лямках экзоскелета при λ = -12; µ=-35 Таким образом, в случае демпфирования силы, моменты и прочие кинематические характеристики изменяются более плавно, а их максимальные значения меньше, чем при отсутствии демпфирования. Заметим, что при увеличении коэффициентов демпфирования больше 0,2 с-1 качество процесса заметно ухудшается и процесс теряет устойчивость. То же самое наблюдается и при уменьшении этих коэффициентов от значения 0,1 с-1 . Иными словами, можно подобрать некоторый диапазон коэффициентов демпфирования, при котором получаются приемлемые переходные процессы. Отдельно отметим энергетические затраты человека-оператора при реализации движения с помощью идеальных коленных двигателей. В случае нагрузки в 50 кг эти затраты составляют 118 Дж для вариантов, представленных на рис. 9–11. В случае нагрузки в 100 кг эта же величина составляет 132 Дж. Биомеханический функционал затрат энергии человеком-оператором определялся формулой [2] T W = J^|momi • фddt, 0i где momi - развиваемые человеком межзвенные моменты сил, ф; - межзвенные углы человека в суставах. Построение законов управления и результаты численных исследований В ЗАДАЧЕ УПРАВЛЕНИЯ ГИДРОЦИЛИНДРАМИ В КОЛЕННЫХ ШАРНИРАХ Одной из возможных реализаций активного движения экзоскелетона является использование гидравлического привода. Система состоит из двух гидроцилиндров, конструктивно расположенных между бедрами и голенями экзоскелетона, поршни которых, осуществляя поступательное движение, обеспечивают угловое перемещение в коленных шарнирах. Движение экзоскелетона описывается в этом случае динамической системой (4), (5), а также приводимыми ниже уравнениями, отвечающими за работу гидроцилиндров. Цилиндр имеет две полости, в которые под управлением трехпозиционного сервораспределителя (золотника) поступает (либо не поступает) поток гидравлической жидкости от гидронасоса, поддерживающего давление PS = const. Тем самым, например, в поршневой полости давление P равно P = PS, а в штоковой - атмосферному P2 = ps. Возникающее в результате работы гидроцилиндра усилие Fg, давление в полостях P1, P2 и удлинение штока l взаимосвязаны; когда высокое давление подается в поршневую часть, они описываются [7–9] уравнениями d2l dt2 17 (P A -PA,) MpL - dl w - Fg dt dP1 =_p_ dt A1l -Ad-Cp(P, -P) + CdS dt dP2 = p dt ” A2(Lg -1) A, d- + Cp(P1 -P,) dt где A1, A2– площади поршней соответственно в поршневой и штоковой полостях; w – коэффициент трения; в - объемный модуль упругости масла; C ip, cd - некоторые Рис. 12. Схема работы гидроцилиндра в коленном шарнире коэффициенты; ρ – плотность масла; s > 0 – регулируемая золотником площадь отверстия для подачи и откачки масла в полостях; Lg – предельная длина штока; M ρ – масса штока. Аналогично уравнения (11) выглядят и при подаче высокого давления в штоковую полость. В дальнейшем для простоты предполагалось, что Mρ = 0, поэтому из первого соотношения в (11) имеем Fg =(P1A1-P2A2)-wdl, dt(12) dF dP dPd g =(A11-A22)-w . dt 1dt 2dtdt Работа гидроцилиндра связана с перемещением штока, который либо увеличивает, либо уменьшает межзвенный угол ϕmin≤ϕ≤π в соответствующем коленном шарнире. Геометрия установки гидроцилиндра влияет на то, как будут связаны между собой удлинение штока l и упомянутый угол ϕ . При численном исследовании была принята следующая кинематическая схема расположения гидроцилиндра DEF на экзоскелете (рис. 12), где прямая AD перпендикулярна AO , а CB – OB, удлинение штока l есть отрезок DE, длины всех отрезков, см: FC = 0; EF = 25,5; DA = CB = 3,5; AO = 14; OB = 33,5. Поэтому DC=l+25,5= J 1330,5-913,5cosϕ-332,5sinϕ. Расчеты показывают, что при этом плечо силы, развиваемой гидроцилиндром hL (ϕ) относительно коленного шарнира, меняется от 35,1 см при угле ϕ =180° до максимального значения 14,52 см при ϕ =84°, а затем убывает до значения 13,65 см при минимально возможном угле ϕ = ϕmin=66°. Сформулируем задачу управления гидросистемой экзоскелетона, цель которой обеспечить требуемое угловое движение в коленных шарнирах и одновременно реализовать необходимое силовое воздействие между голенью и бедром. Управление гидроцилиндрами будет основано на отслеживании идеальных моментов, которые обозначим как U1⊗, U2⊗; они были получены выше в предыдущем разделе; управляющей функцией является величина площади открытия отверстия гидрораспределителя s. Для реализации этого алгоритма необходимо вычисление производных желаемых моментов U1⊗, U2⊗; в данном алгоритме они вычислялись разностным способом. Знание в каждый момент времени значения текущего межзвенного угла ϕ , а значит и текущего значения плеча hL (ϕ) позволяет вычислить «идеальную» силу штока Fg⊗, отвечающую тому или иному идеальному моменту U⊗, а dFg⊗ также . dt В формуле (11) фигурирует первая и вторая производные удлинения поршня dl d2l и . Первую производную можно получить из показаний датчика угла и угловой dt dt2 скорости и учета геометрии расположения гидроцилиндра. При моделировании используемую вторую производную удлинения l приходится учитывать приближенно, рассматривая ее значение с предыдущего шага интегрирования совместной системы, составленной из (4), (5), (12). Следует отметить, что применяемые в механизме гидроцилиндры являются гораздо более мощными и малоинерционными двигателями, чем, скажем, электродвигатели. Поэтому корректно поставленная задача их моделирования требует, в отличие от электродвигателей, использования примерно в сто раз более мелкого шага интегрирования: здесь применялся в основном шаг в т = 10-5 с. Это еще один аргумент в пользу возможности использования в соотношениях d2l (12) приближенного значения . dt2 При построении закона управления будем обеспечивать выполнение закона отклонения текущего значения силы Fg от ее желаемого значения F® (t) в виде dFg _ dFg8 X< 0. -77 /J' F — F ) + —г", dt ggdt С учетом (11) и (12) это приводит к линейному условию для определения управления – площади отверстия гидрораспределителя s. При численных исследованиях были приняты следующие величины параметров гидроцилиндра: P = 1600 МПа; A = 4п см2; A = 3п см2; Ps = 7,51 МПа; р = 850 кг/м3; С ip = 10 см5/№с; w = 0,0005 Н-с/см. Кинематическая вязкость масла µ принималась равной 100 мПа∙с, предельная величина управляющего параметра s гидросистемы hole = 0,12 см2. В результате синтеза были получены необходимые управляющие воздействия в виде площади открытия золотника, значения которых использовались в полной динамической системе (4, 5, 11). Ниже приведены графики переходных процессов экзоскелета, моменты, развиваемые гидроприводами, и силы взаимодействия человека и экзоскелетона; звездочками указаны графики, отвечающие желаемым процессам. Численные эксперименты проводились при следующих параметрах: Х = -10 000 с-1, P = 50 кг, С = 250 Н/см (вариант А) и / = -100 000 с-1, P = 50 кг, С = 250 Н/см (вариант В). В обоих вариантах kd = 0,1 с-1. Режимы на рис. 13, 15, 17, 19, 21 отвечают варианту А, им противопоставляются соответствующие графики на рис. 14, 16, 18, 20, 22, отвечающие варианту В. Анализ полученных результатов показывает заметное влияние коэффициента X на точность исполнения экзоскелетоном заданного движения. Видно, что при Х =-100 000 с-1 точность реализации движения и, соответственно, степень вычислительной устойчивости на рис. 14, 16 выше, чем при χ = –100 000 c–1 на рис. 13, 15. Из рассмотрения графиков на рис. 17, 18 следует, что величины управляющих моментов в гидроприводе в случае А почти в два раза превышают величины этих же моментов, полученных в случае B. Это объясняется тем, что отклонения, возникающие в углах и угловых скоростях, во втором случае меньше, чем в первом. Отметим, что график управляющего момента на рис. 18 гораздо ближе к графику управляющего момента, развиваемого идеальным двигателем на рис. 10; а силовое воздействие на рис. 20 полностью соответствует силам на рис. 11. Это подтверждает правильный выбор порядка коэффициента χ и соответствующего ему шага интегрирования τ в варианте B. Поскольку биомеханический функционал затрат энергии (10) зависит одновременно как от кинематических параметров, так и от управляющих моментов, то следует ожидать, что энергетические затраты при значении χ = –100 000 c–1 должны быть близки к соответствующему значению функционала в случае идеального двигателя. Действительно, величина W для режима на рис. 18 в случае нагрузки в 50 кг составляет W = 118,6 Дж, а в случае нагрузки в 100 кг W =130 Дж. Рис. 13. Графики углов в опорной ноге экзоскелета Рис. 14. Графики углов в опорной ноге экзоскелета Время, с Рис. 15. Графики угловых скоростей в опорной ноге экзоскелета 16. Графики угловых скоростей в опорной ноге экзоскелета Управляющие моменты, Н м Управляющие моменты, Нм ч Угловые скорости о опорной ноги, % Время, с Рис. 17. Графики управляющих моментов Рис. 18. Графики управляющих моментов Рис. 19. Графики сил, возникающих в крепежных лямках экзоскелета Рис. 20. Графики сил, возникающих в крепежных лямках экзоскелета Рис. 21. Графики управляющих величин площадей гидрораспределителя Время, с Рис. 22. Графики управляющих величин площадей гидрораспределителя Выводы 1. В работе построена динамическая модель экзоскелетона, управляемого как моментными двигателями в коленных шарнирах, так и с помощью силового воздействия от упруговязких лямок, осуществляющих связь некоторых точек тела человека-оператора с механизмом. Человек также испытывает воздействие со стороны лямок, но за счет собственных мышечных усилий он поддерживает заданный режим ходьбы. При численных исследованиях этим заданным режимом считался плоский одноопорный комфортабельный режим ходьбы. 2. В случае идеальных моментных двигателей синтез проводился по полным уравнениям динамики; формально он обеспечивал требуемое качество движения по желаемым траекториям в коленных шарнирах экзоскелетона, однако высокое качество реализации желаемого режима ходьбы было достигнуто не только по углам нижних конечностей, но и по положению корпуса аппарата. В результате моделирования выявлено существенное влияние коэффициентов демпфирования и упругости в лямках. Отмечена важность того факта, что при моделировании необходимо учитывать наличие мягких и твердых тканей в теле человека в точках крепления лямок. 3. Построена модель экзоскелетона, управляемого гидроприводами в коленных шарнирах. Синтез проводился с учетом полных уравнений динамики экзоскелетона, гидросистемы и учитывал упруговязкие свойства лямок. Построено управление, которое одновременно реализует с требуемым качеством как желаемые перемещения в коленях, так и необходимые усилия, которые должны развивать гидроцилиндры. 4. Моделирование экзоскелетона с гидросистемой выявило существенную роль взаимосвязи коэффициента усиления в алгоритме управления по силе и шага интегрирования на устойчивость вычислительного процесса. Переход на значительные коэффициенты усиления позволяет учесть скоростные процессы, присущие гидросистеме, в отличие от более медленных инерционных процессов в механической конструкции аппарата. Корректность результатов подтверждена совпадением решений модели с гидросистемой со случаем идеальных двигателей. 5. При выборе конструкции гидроцилиндра следует учесть, что плечи сил относительно коленных шарниров, на которых работают гидроцилиндры, могут не являться монотонной функцией межзвенного угла. Это может привести к недостатку усилий, вырабатываемых гидроцилиндрами на определенных силовых режимах движения. Приложение При численном исследовании задачи в качестве модели тела человека была рассмотрена следующая среднестатистическая модель [6]: рост – 1,747 м, масса – 73,4 кг; длины бедер, голеней и корпуса соответственно равны 0,514; 0,402 и 0,741 м; их массы соответственно 9; 2,9 и 47,6 кг (масса стоп – каждая по 1 кг, высота голеностопного сустава над поверхностью 9 см); а, = 0,245 и Ь,= 0,161 м. Корпус человека считался равномерно распределенным по массе, исходя из этого подсчитывались величины Kr и J . Значения других моментов инерции: центральный момент инерции бедра – 0,1662 кг∙м2, центральный момент инерции голени – 0,0357 кг∙м2. Масса экзоскелетона была принята равной 15 кг: 5 кг – масса корпуса, по 2,5 кг – масса каждого из бедер и голеней, причем их масса всюду распределена равномерно. Благодарности Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований, гранты № 12-01-00800-а и № 15-01-04503-а.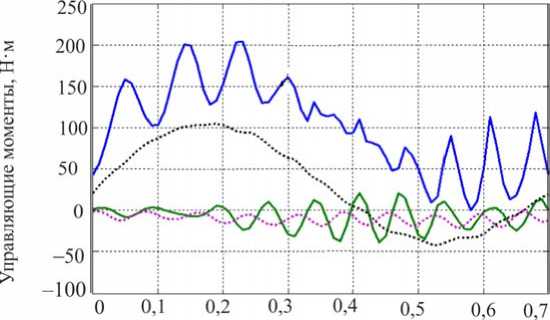
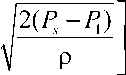
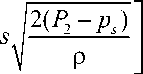
Список литературы О задаче организации ходьбы экзоскелетона нижних конечностей при помощи управления в коленных шарнирах
- Белецкий В.В. Двуногая ходьба. -М.: Наука, 1984. -286 с.
- Белецкий В.В. Плоские линейные модели двуногого шагания. -М., 1973. -(Препринт Ин-та прикладной математики им. М.В. Келдыша АН СССР).
- Лавровский Э.К., Воронов А.В. Определение масс-инерциальных характеристик ноги человека//Физиология человека. -1998. -№ 2. -C. 91-101.
- Лавровский Э.К., Письменная Е.В. Алгоритмы управления экзоскелетоном нижних конечностей в режиме одноопорной ходьбы по ровной и ступенчатой поверхностям//Мехатроника, автоматизация, управление. -2014. -№ 1. -C. 44-51.
- Письменная Е.В., Кузмичев А.В., Митрофанов И.Е., Иванов А.В., Кузнецов А.С. Устройство помощи при ходьбе: Патент на полезную модель № 139266 РФ. -№ 2013143671/12; заявл. 27.09.13; опубл. 10.04.14. -Бюл. № 10. -4 с.
- Формальский А.М. Перемещение антропоморфных механизмов. -М.: Наука, 1984. -368 с.
- Abbot R.D., McLain N.W., Beard R.W. Validation of synthesis technique for the optimal control of an electro-hydraulic position system//ASME J. Dyn. Sys., Meas., Control. -2000. -Vol. 123. -P. 377-384. DOI: DOI: 10.1115/1.1387446
- Merritt H.E. Hydraulic Control Systems. -New York, USA: Wiley and Sons Publishers, 1967.
- Muvengei M., Kihiu J. Bond graph modeling of inter-actuator interactions in a multi-cylinder hydraulic system//World Academy of Science, Engineering and Technology. -2011. -№ 73. -P. 32-41.


