О задаче теории теплопроводности с одной теплоизолированной границей
Автор: Каркусты Н.Н.
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.1, 1999 года.
Бесплатный доступ
В статье рассмаривается изотропная однородная область, на части границы которой задается теплообмен со средой. Задача приводится к сингнулярно-интегральным уравнениям типа Винера - Хопфа, решение которых осуществляется методом факторизации.
Короткий адрес: https://sciup.org/14317991
IDR: 14317991
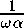
Список литературы О задаче теории теплопроводности с одной теплоизолированной границей
- Нобл Б. Применение метода Винера-Хопфа для решения дифференциальных уравнений в частных производных.-М.: ИЛ, 1962.-279 с.
- Мусхелишвили Н. Н. Сингнулярные интегральные уравнения.-М.: Наука, 1968.-511 с.
- Каркузашвили Н. Н. Задача о неустановленном температурном поле в неограниченной пластинке со смешанными граничными условиями//Некоторые вопросы прикладной математики.-Киев: Наук. Думка, 1971.-Вып. 1.-C. 52-57.
- Коваленко А. Д. Основы термоупругости.-Киев: Наукова Думка, 1970.-307 с.
Статья научная
