Об аналоге задачи Трикоми для уравнения третьего порядка смешанного типа

В современной концепции уравнений в частных производных (УрЧП) большое значение имеет изучение уравнений смешанного типа.

Поставим задачу. Исследуем следующее уравнение:

'u xxx ^- u y ^{- 2} u = О, У >  О,

‘                                                                     •

_uxx - uyy + 2u = 0, У < 0, где 21,2 - числовые параметры в некоторой конечной области D плоскости (x, у), образованной следующими линиями: 1) в полуплоскости у > 0 отрезками AA, BBY, AB, лежащими на прямых x = 0, x = 1, у = h, А(0,0), А1(0, h), В(1,0), В1(1, h); 2) в полуплоскости у < 0 двумя характе- ристиками уравнения (1):

AL : x = - у , BL : x - у = 1, исходящими из определенной точки

L

— —

Область D разделена на две части: D 1 = D п ( у >  0) - это параболическая часть смешанной области D; uD₂ = D п ( y <  0) - гиперболическая подобласть области D •

Задача 1. Требуется отыскать функцию u(x,y) , обладающую указанными свойствами:

• 1)    u ( x , у ) е С ( D ) п С ¹ ( D и АА 1 ) п C x ^ у ^1} ( D 1 ) п C ² ( D ₂ );

• 2)    u ( x , у ) является регулярным для уравнения (1) решением в области D ;

• 3)    u ( x , y ) отвечает требованиям краевых условий:

^{u (0,} y ) = Ф 1⁽ y ), u (1, y ) = ф _г ⁽ y ), u x (1, y ) = ф _ъ ⁽ y ), 0 < y < h ,

u (x, -x) = ^(x), 0 < x <  , где ф(х) - функция, непрерывная совместно со второй производной, при этом

^ (0) = ф (0); ф ( y ), ф ₂ ( y ), ф ₃ ( y ) - данные непрерывные функции [1].

Определение. В области D для уравнения (1) регулярным решением вышеуказанной задачи называется всякая функция u (x, y) е С (D) п С1 (D и АА1) n Cx3y1} (D1) n C2 (D2), удовлетворяющая краевым требованиям (2) и (3).

Предположим, что:

2 1 >  ( - 2 2 )², 2 1 > 2 3 + 3 2 2 n ², 2 1 >  0.

Можно ввести новую некоторую неизвестную функцию

• v ( x , y ) = exp( - p x ) u ( x , y ),                                    (4)

где p = const >  0.

Уравнение (1) в итоге станет таким:

u_vvy - u _v + 3 p v ,._v + 3 p u _v + ( p - 2 ) u , y >  0,

0 = L 0 ( u ) = ^

xxx     y        xx          x             1

^U xx ^{- u} yy ^{+ 2} P^U x ^{+ (} p ^{2 + 2} 2^{) u} , y <  ⁰ ,

Теорема. Если u(x, y) есть регулярное решение однородной задачи 1, то при соблюдении требований 1) или 2) решение u(x, y) в области D тождественно равно нулю [1].

Доказательство. Потребуем на концах интервала x = 0 и x = 1 выполнения следующего до- полнительного условия:

lim u ( x ,0) [ u xx ( x ,0) + p u x ( x ,0) 1 = lim u ( x ,0) [ u xx ( x ,0) + p u x ( x ,0) 1 = 0

x ^0+                              x ^1-0

Перейдем в области D ₂ к характеристическим координатам Ь = x + y, п = x - y . Тогда уравнение (5) при y <  0 станет

L0(u) = u^ + p(4f + un) + p + 22 u = 0, а область D2 будет отображена с областью А = {(^, п) 10 < ^ < п < }1 •

Рассмотрим тождество

0 = 4uL0(и) = (2иип + pu2)^ + (2ии^ + pu2)п + (p2 + 22)и2 - 4и^ип .(8)

Выразим из уравнения (7) и ^ и в правой части (8) изменим последний член:

„        z 4 _{2х    z}„      p ² + 2 2 _х2    ( p ² + 2 2 ) ² ₂

-4ufип =(— ип )^ + (2ип + —^---u)-- p             2p4

Тождество (8) перепишем в виде, учитывая последнее равенство:

0 = 4 u L ₀( u ) = (2 uu + pu ² + — u 2 К + (2 uu + pu ²)„ + (2 u + ^{p + 2 2} u )² + ^{( p + 2} 2 ^{) (} 3 ^p —² 2⁾ u ² .(9)

• 0           п         p n ль v    ь        п v п     2p4/^2

Взяв точку ( x , x ) (0 <  x <  1) на прямой n = Ь , проведем через эту точку характеристику n = x уравнения (7).

Через А _x «отметим» область, которая ограничена отрезками прямых п = х, п = Ь , Ь = 0. По этой области А _x проинтегрируем тождество (9):

xxx

2ju( t ,0)uy (t ,0) dt = 2ju(^,b) [Чг (Ь, Ь) - Un (Ь, Ь)] db = - J u^,^ db +

0                    0

О 2+2.             xx

+ j (2un + P—2 и)2 d^dn + рj U2 (£ x)d^ + и2 (x, x) +

A _x          ^{2 P}               0

Рассмотрим в области D тождество:

(р 2+х^^Чзр2 — 22)

4 р ²

j и2 d^dn > 0.

a x

u(uxxx — Uy + 3PUxx + 3р Ux + (р2 — 21)u) = (uUxx — 1 U2 + 3IU2 + 3 р 2U2) x —

—uuy — (3ри2 + (21 — р 3)u2) = 0.

Вдоль A ( e , h ) B (1 — e , h ) ( h , e — как угодно маленькие числа, большие нуля) проинтегрируем (11) по х, а потом перейдем в полученном равенстве к пределу h ^ 0 и e ^ 0. Принимая во внимание условия (6), в итоге имеем равенство

j и ( x,0) u _y ( x ,0) dx =

Из неравенств (10) и

< - и_х' (1,0) + J [3 ри_х ² ( x , 0) + ( 2 — р ³ U ² ( x , 0)] d } x .

1 ² x        0      x

из (12) имеем

b j z 2 (x) dx <

a

2 b

a

u x (1,0) + 2 j [3 р + ^{2 1} P ) ] u x ( x , 0) dx <  0.

0        ⁿ

В (10) и (12) положим теперь р = 3 2 или р = — 2 2 .Тогда и (1,0) = 0, и ( x ,0) = const. Отсюда следует, что и ( x , y ) = 0. Из выражения (4) тогда получим, что u ( x , y ) = 0.

Изучим тождество в области D :

u ( u^ xxx

—

u., — 2 u ) = ( uu^ — ¹ u ²)_x — (1 u ² ) y 1 / v xx       x / x v 2

—

2 u ² - 0.

Это тождество интегрируем по области D₁ и с учетом того, что ^ (0) = ф ₂ (0) = ^ (0) = 0, получим:

^{— 2} j [( ^uu xx “1

—

¹ u_x )x xx

—

• 1                           rr

(— u ²) — 2 u ²] dxdy ^ J^ u ²( x , h ) — u ²( x ,0) J dx +

• ²     y                0^L

b

+ j u 2 (1, y ) dy + 2 2 ₁ j u ²( x , y ) dxdy = 0.

^П 1

Из-за того, что u ( x ,0) = 0, из формулы (13) имеем, что u ( x , h ) = 0 и u_x (1, y ) = 0, однородная

u ( x , y ) ^ 0, V ( x , y ) e D 1 . Задача Дарбу u ( x ,0) = 0, u ( x , — x ) = 0 в области D 2 для уравнения (1) при y <  0 имеет только тривиальное решение u ( x , y ) = 0, V ( x , y ) e D ₂ . Значит, u ( x , y ) ^ 0 в D .

После этого докажем существование решения задачи 1. Для этого нужно перейти к лимиту (пределу) при y ^ 0 + в уравнении (1) и принять к сведению краевые условия (2), [1]:

т (x) — 21т(x) = v(x),(14)

т(0) = ^(0),т(1) = ^2(0),т (0) = ^3(0),(15)

где т ( x ) = u ( x , 0), v ( x ) = u_y ( x , 0).

Применяя трёхкратное интегрирование к равенству (14) и принимая во внимание (15), составим функциональное соотношение между т ( x ) uv ( x ), принесенное из части D 1 на y = 0:

т( x) — 21 x (x — t )2т( t) dt = 1 x (x — t )2 v (t) dt +1 т" (0) x2 + ^ (0) x + ^ (0),(16)

2 0                  20

где т (0) = -21 j (1 -t)2 т(t)dt -J (1 -t)2 v(t)dt - 2^3 (0) - 2^1 (0) + 2^2 (0).

Заранее предполагая, что правая сторона равенства (16) известна и равна выражению q ( x ), имеем интегральное уравнение Вольтерра второго рода для т ( x ) [1]:

x

т ( x ) = q ( x ) +— J( x - 1 ) ² т ( t ) dt . ²0

После обращения уравнения (17) имеем:

x

т ( x ) = q ( x ) + 2 J R ( x , t ) q ( t ) dt ,

.

где R ( x , t ) есть резольвента ядра ( x - t ) , 2 = -y

Принимая в расчет значение q(x) в (18), получаем x                                2    2

т ( x ) = Mm ( x , t ) v ( t ) dt + т (0)[— + —

J                        2   2

где

J R ( x , t)t ² dt ] + ^ ₃ (0) [ x + 2 J R ( x , t)tdt ] + ^ j (0)[1 + 2 J R ( x , t)dt ] ,(19)

x

x

x

1      2

М ( x , t ) = — ( x - 1 )² + — J R ( x , t 1 )( 4 - 1 )² dt 1 ] .

t

Теперь принесём из гиперболической части D ₂ на линию у = 0 функциональное соотношение между т ( x ) и v ( x ). Чтобы его получить, проанализируем для уравнения (1) при у <  0 решение задачи Коши т ( x ) = u ( x ,0), v ( x ) = u_y ( x ,0). Следуем [2]:

u ( x , У ) =

т ( x - у ) + т ( x + у ) ₊ 22^ Уy x + y I ^{1 (} V ^{2 2} - ^{У   (} x   ^{5 )} . )

2        ⁺  2 ^{J          2} -/v- _ЛA²

-т ( ^ ) d ( 5 ) +

+-

—

где 1 0 ( z ) и 1 1 ( z ) - функции Бесселя мнимого аргумента нулевого и первого порядков.

Если (21) удовлетворит краевому условию (3), то получится интегральное уравнение типа Вольтера x    x d

^{T ( x} ) = p ^{( x} ) ^- J ^{т (} ^ ) - — I 0⁽^ Z^ C x ”)) ^{d 5} 0      ^{5 d} x

где

x

x

p ( x ) = 2 ^ I - I- ^ (0) + J 1 0 ( 42 2 5 ( x - 5 )) v ( 5 ) d 5 .

< ² ^          0

Предполагая p(x) известной и применяя формулу обращения для уравнение типа (22), будем иметь [1]:

x

т ( x ) = J J 0 (V 2 T( x - 1 )) v ( t ) dt + g ( x ),

где x ' (t

g ( x ) = - [ ^ I - | J q [ 2 2 V x ( x - 1 ) ] dt .

0   1 ² )

Принимая во внимание значение т (0), равенство (19) перезапишем так:

x  11

т ( x ) = J М ( x , t ) ^v ( t ) dt + J Q ( x ’ t T( t ) dt + j ^ ( x , t ) v (t ) dt + g ( x ),                   (25)

где

x

Q ( x , t) = Я^( x , 1 ); 3 ( x , t) = - -( x ² + Я J R ( x , 1 )t ² dt )(1 - 1 )²;

g (x) = ( ^ (0) - ^(0) - ^ ₃ (0))( x ² + Я J R ( x , 1 ) 1 ² dt) + ^ 3 (0)( x + Я J R ( x , t ) tdt + _{Ф 1} (0)(1 + Я J R (x , 1) dt ).

0                                00

Из (23) и (25) «устраним» т(x). Тогда получим для нахождения v(x) интегральное уравнение первого рода:

x                                 x1

J Jо (^Я^ (x -1)) v (1) dt = J М (x, t) v (t) dt + J Q (x, t) v (t) dt +h (x),(26)

0                               00

Q ( x , 1 ) = 3 ( x , 1 ) + J Q ( x , t 1 ) J 0 (,ДГ( t 1 - 1 )) dt 1 ; h ( x ) = J Q ( x , 1 ) g ( 1 ) dt + g ( x ) - g ( x ).

t0

Так как в смысле гладкости резольвента R(x, 1) поступает также, как ядро (x -1)2 , то учиты вая свойства заданных функций фi (у), i = 1,3, ^(x), функции M(x, 1), Q(x, 1) непрерывны совместно с частными производными первого порядка по аргументам x ut; h(x) непрерывна вместе с производной в областях своего определения, притом что M(x, x) = 0, J0(0) = 1.

Найдя производную по аргументу x от уравнения (26), приходим к смешанному интегральному уравнению. Обратим его, как интегральное уравнение Вольтерра второго рода:

v ( x ) = J Г ( x , t ) v ( t ) dt + h 1 ( x ),                                     (27)

где ядро Г ( x , t ) и его правая часть h 1 ( x ) выражаются в терминах резольвенты R ( x , t ) ядра ( x - 1 )² и данных функций ф _i ( y ), i = 1,3 ^ ( x ), при том Г ( x , t ) е C ( [ 0,1 ] х [ 0,1 ] ), h 1 ( x ) g C [ 0,1 ] .

Как видно, выражение (27) есть интегральное уравнение Фредгольма второго рода. Из единственности решения исходной задачи вытекает разрешимость этого уравнения. Таким образом, функцию v ( x ) можно определить из уравнения (27). Далее, найдя функцию v ( x ), в области D 2 по формуле (21) определим решение u ( x , у ) задачи, а в D 1 как решение уравнения (1) при у >  0 с краевыми условиями (2) и u ( x ,0) = т ( x ).

Решение задачи (1) и (2), u ( x ,0) = т ( x ) удовлетворяет интегральному уравнению, согласно

[1]:

Я 1

u (x, у) = и 0 (x, у) —1J d ^ G (x, у; ^, n)z (^, 7) dn, п 0)0

' уу

/ А 1

^и 0⁽ x , у ) = -1 п

J Gy;(x, у; ° n)^1 (n)dn - J G^(x, у; ° n)^1 (n)dn -. 00

у1

-J G;;(x, у ; 1, n)^2 (n) dn + J G;(x, у;;, 0)^(;) d};, 00

где G(x, уУ,п) есть функция Грина краевой задачи (1), (2), и(x,0) = т(x) уравнения ихх-- иу = 0.(29)

xxxy

Эта вышеупомянутая функция Грина G(x, уУ,п) описывается посредством фундаментальных решений (29):

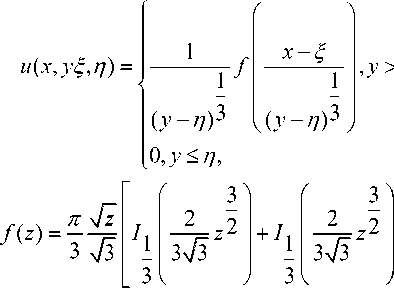
n , v ( x , y ^,n ) =

-_z x   n Zz

^{, ф ( z} )  3 V3

1    -( x - £ 7

---------г ^1 --------- I

¹ I ⁽ y ^- n ) 7

⁽ y ^- n ⁾³

0, y <  n ,

(      3 7

2 з

3Гзz

V        7

y > n ,

(      3 7

2 з

3V? ^z

V       7

где I_v ( z ) - функция Бесселя. Функции f(z) и ф (z) именуются функциями Эйри и удовлетворяют уравнению t ( z ) + zt ( z )/3 = 0.

В [2] рассмотрена однозначная разрешимость уравнения (28), а по формуле (21) можно решить задачу Коши.

При вышесказанных предположениях относительно   λ₁  и   λ₂ , а именно при

2 1 >  ( - 2 2 ) ² , 2 1 >- 2 ^ + 3 2 2 n ², 2 1 >  0 исследована однозначная разрешимость поставленной задачи для смешанного гиперболо-параболического уравнения третьего порядка со спектральным параметром.