Об аномальной дисперсии звука и структуре жидкости

Исследования скорости звука в жидкостях обнаруживают присутствие аномальной (положительной) дисперсии звука [1–3], т.е. превышение скоростью звука гидродинамического значения при больших частотах. Эта особенность исчезает при понижении плотности, и распространение звука в жидкости становится сходным с таковым в газе. Исчезновение аномальной дисперсии наблюдается и в сверхкритической области температур, т.е. этот эффект не связан с критическими явлениями, поэтому представляется интересной попытка установить связь между изменением характера коллективного движения и изменениями, происходящими в структуре жидкости.

В работе были исследованы структуры различных компьютерных моделей: модели твердых сфер с параметром упаковки от 0,1 до 0,6; модели жидкости Леннард-Джонса (Л.-Дж.) для набора температур и плотностей; модели расплавов Cs, Rb, Hg для ряда температур, охватывающих весь диапазон существования жидкой фазы. Модели реальных систем (Cs, Rb, Hg) были получены по данным дифракционных экспериментов и описаны ранее [4, 5]. Для анализа моделей использовался метод Вороного-Делоне [6], заключающийся в разбиении пространства на простые геометрические фигуры с их последующим статистическим анализом.

Изменение характера коллективного движения происходит при достаточно низких плотно- стях, поэтому анализ изменений в структуре моделей производился в терминах межатомного пространства. Каждый симплекс Делоне относился к одному из 5 классов (n0, n1,…, n4) в соответствии с объемом и формой межатомного пространства в нем [7]. Симплексы n0, n1, n2 являются элементами плотных структур (n0 и n1 – близки к правильному тетраэдру, а симплексы n2 – к четвертинке октаэдра). Симплексы n3 и n4 являются фрагментами искаженных, рыхлых структур, они появляются в нагретых кристаллах и жидкостях [7]. По типу преобладающих в системе симплексов модели были разделены на три класса: I – модели с плотной структурой (плотная жидкость), II – модели со структурой с появляющимися границами между сгустками атомов (переходная область), III – модели с неоднородной структурой, состоящей из плотных и рыхлых фраг- моделей на классы с различной

Рис. 1. Фазовая диаграмма системы Леннард-Джонса. Закрашенные знаки – аномальная дисперсия звука [1]

ментов (рыхлая жидкость). Подробно методика разделение структурой была описана ранее [7].

Во всех системах было обнаружено сходное изменение значений параметров n i с уменьшением плотности и ростом температуры [4, 7]. При движении вдоль кривой равновесия жидкость–пар к критической точке области I, II и III последовательно сменяют друг друга. Различия проявлялись в положении областей I, II и III на фазовой диаграмме.

Для системы Л.-Дж. фазовая диаграмма (радиус обрезания потенциала 2,5 σ ) в координатах ( ρ / ρ c , T / T c ) с нанесенными на нее областями I, II и III приведена на рис. 1. Полученная информация о структуре была соотнесена с данными о нормальной и аномальной дисперсией звука для Ne, N 2 , O 2 т.к. для этих веществ бинодаль совпадает с бинодалью системы Л.-Дж. в приведенных координатах.

Закрашенные знаки на рис. 1 соответствуют наличию в системе аномальной дисперсии звука. Можно заметить, что смена геометрии ближнего порядка непосредственно связана с изменением дисперсии. Сходные изменения происходят в расплавах металлов. На рис. 2 приведена фазовая диаграмма для Hg и отмечены области с различным ближним порядком. Аномальная дисперсия звука наблюдается в областях I и II [3]. В рубидии скорость звука исследовалась для температур 313-600 К, соответствующих плотной жидкости, и наблюдалась его аномальная дисперсия [2].

Присутствие и исчезновение аномальной дисперсии может быть объяснено изменением характера коллективного движения частиц. В жидкости при высоких плотностях у временной корреляционной функции скоростей (ВКФС) существует протяженная область отрицательных значений [8], что говорит о смене направления скорости частицы при столкновении с ее окружением. При низких плотностях ВКФС принимает только положительные значения, т.е. частица при соударении увлекает окружение в сторону своего движения. Это приводит к образованию тороидального вихря аналогичного гидродинамическому [9]. Методом МД моделирования было найдено, что для системы твердых сфер изменение характера коллективного движения происходит в окрестности плотности упаковки f ≈ 0,39 [8]. Наши исследование показали, что в этой же окрестности ( f ≈ 0,35) мы наблюдаем переход от плотной структуры жидкости (область

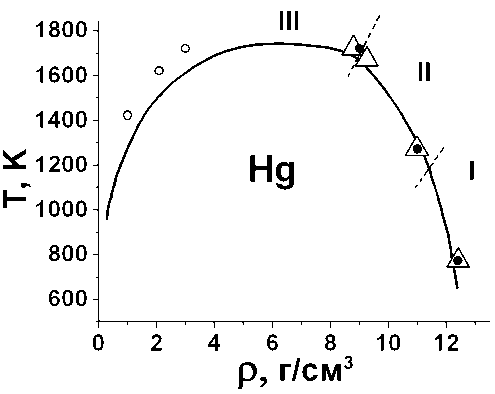
Рис. 2 Фазовая диаграмма ртути:

V – исследуемые модели, o – состояния, в которых исследовалась дисперсия звука [3], • – аномальная дисперсия звука

• I)    к рыхлой (область III). Такая же особенность ВКФС присутствует в цезии при температуре около 1000 К [10], что соответствует обнаруженному нами изменению структуры [4].

Таким образом, можно говорить о том, что исчезновение аномальной дисперсии звука и изменение типа коллективного движения в жидкостях разной природы связано с изменением структуры жидкости и ее переходом от плотной жидкости к жидкости «рыхлой».

Работа поддержана РФФИ, проекты 06-03-32690, 06-08-01142.