Об аппроксимации нестационарных уравнений мелкой воды

В настоящей работе рассмотрена математическая модель движения жидкости, полученная путем применения усредненных по вертикали характеристик (так называемых уравнений мелкой воды).

Основные уравнения движения жидкости при упрощениях, в результате которых получаются уравнения мелкой воды, можно записать в виде [2]

eg ! с(рЯ) _ ₀

ex ct                                  (1)

Ct

Граничные и начальные условия для этой системы име- ют вид

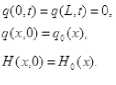
Здесь q – поток количества жидкости (масса жидкости, приходящаяся на единицу длины и времени), ρ – плотность жидкости, H – возвышение свободной поверхности; ,

B*_v=q^p^ cosS- 4~~4- -pg-H— -H^ c pH Ex Ex

– коэффициент ветрового напряжения; ρ_a – плотность воздуха; W – скорость ветра, ϑ – угол между осью x и направлением ветра; g – ускорение свободного падения, c – коэффициент Шези; p_a – атмосферное давление, L – длина водоёма (масштаб длины).

Для решения задачи удобно перейти к безразмерным переменным (атмосферное давление, плотности воздуха и жидкости полагаются постоянными):

X = Lxb, t=Tt\ H=NHb, W=KfTb, q = Qqb.

Здесь

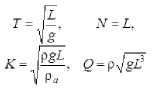
есть масштабы времени, высоты свободной поверхности, скорости и потока соответственно (в дальнейшем верхний индекс «b» у безразмерных переменных опуска- ется).

Отметим, что ранее в работах [3-6] были рассмотрены стационарные уравнения мелкой воды. При этом уравнения (1) были сведены к уравнению Пуассона относительно функции тока, решение которого искалось методом взве- шенных невязок.

Для решения нестационарных уравнений (1) воспользуемся методом частичной дискретизации [7]. Приближённое решение будем искать в виде линейной комбинации базисных функций, при этом коэффициенты разложения будут зависеть от времени q =, q = q0 (л) + V Q t (f)Nqk (x),

~                                         (3)

H^H-H^ + Vb^N^xy где M – количество базисных функций, ak , bk – искомые коэффициенты разложения, q0(x) и H0(x) – поток и высота уровня жидкости в начальный момент времени. В качестве базисных функций удобно взять Nqk(x)=xk(1-x), NHk(x)=xk-1. Здесь уже учтены граничные условия (2) в безразмерных переменных:

q(0,t) = q(1,t) = 0

Пусть H^x') =Hg = const , тогда начальные условия для этой системы имеют вид

Я(х;О) = Яо°, g(x;O) = go(x) = O или

^(0) = b_k(0) = О, к = П7.

Рассмотрим подробнее случай, когда для аппроксимации потока и высоты свободной поверхности использованы по две базисные функции. В этом случае (3) примет вид q =»q = a (t)x(l -x) + a₂ (t^x¹ (1 - x), H = H = b_t(t')+b₂(t')x.

Подставляя эти разложения в систему (1), получим согласно методу частичной дискретизации, следующую систему

| [4(й1(,")х(1-х)ч-йг2(Г).г*(1-х))-ТУ* cos-9-

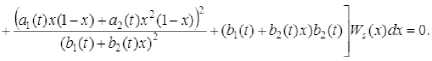
Здесь w_s(x), s = 1,2 – весовые функции.

Отметим, что из-за сложности подынтегральных выражений в данной задаче трудно применить метод Галёрки-на, в котором весовые функции совпадают с базисными. Выберем в качестве весовых функций дельта-функции Дирака (при этом точками коллокации будут являться x₁ = 1/3 и x₁ = 2/3 соответственно). Тогда после вычисления интегралов, входящих в (4), получим систему четырёх обыкновенных дифференциальных уравнений относительно функций a₁(t), a₂(t), b₁(t), b₂(t) :

2 i/ц (t)   2 da_: (t)

9  dt + 27  dt~

2 da, (r) 4 da- (t) _,

9  dt  ~27  dt”

1 .. 1 .. dbdf) 1 db,(t)

• 3    ^w 3        _dtз

• 3          dt     3dt

0.12-- 0.11...........................................................................................................................................................................................

Здесь f_s, s = 1,2 – сложные выражения.

Разрешая указанную систему относительно первых производных от искомых функций, получим задачу Коши с начальными условиями a1(0) = a2(0) = b1(0) = b2(0) = 0.

Для численного решения задачи была составлена программа с помощью математического пакета Scilab [8].

Результаты решения задачи Коши для системы обыкновенных дифференциальных уравнений, описывающей течение мелкой воды, приведены на рисунке 1. В начальный момент времени высота свободной поверхности полагалась равной H₀ = 0.01 ; при этом W = 1, ϑ = 0 .

°Л0   0.2 0.4 0.6 0.8   1

X

Рис. 1 – Высота свободной поверхности

Показан закон изменения высоты свободной поверхности ( H* = 10H ) для двух базисных функций. Разные линии соответствуют разным моментам времени t = 0,06,...,2.4 (снизу вверх).

В дальнейшем предполагается рассмотреть случай, когда искомые функции зависят от двух пространственных переменных и времени.