Об идентификации характеристик неоднородных вязкоупругих тел в рамках модели дробного порядка

Активное использование новых неоднородных материалов, обладающих реологическими свойствами, таких как функционально-градиентные полимеры (ФГП) и полимер-композиты, влечет за собой необходимость построения адекватных моделей их деформирования. Свойства данных материалов зависят от пространственных координат, а под воздействием нагрузок в них протекают процессы ползучести и релаксации, характер которых зависит от внутренней структуры материалов и объемного распределения их свойств. Для учета фактора затухания в материалах со сложной структурой прибегают в том числе к дробно-дифференциальным обобщениям моделей вязкоупругости [1] , которые при меньшем числе параметров являются более точными, по сравнению со стандартными моделями.

Важно заметить, что при изготовлении объектов и конструкций из современных ФГП необходимо оценивать соответствие реальных законов изменения их характеристик относительно изначально спроектированных [2, 3] . Для этого могут эффективно применяться неразрушающие подходы на основе акустического зондирования в режиме установившихся колебаний. Для их реализации требуется разработка адекватных моделей колебаний (в том числе при помощи дифференциальных операторов дробного порядка), описывающих рассматриваемые вязкоупругие объекты с учетом неоднородности их свойств, а также методов решения обратных задач идентификации их функций-параметров [4] .

Развитие моделей вязкоупругих материалов, содержащих производные дробного порядка, берет начало в первой половине XX века в посвященных наследственной упругости работах В. Вольтерра, Х. Больцмана, Ю.Н. Работнова, А.Н. Герасимова и других как отечественных, так и зарубежных ученых. Достаточно подробно история развития моделей дробного порядка и их классификация изложены, например, в работах Ю.В. Россихина [5] , М.В. Шитиковой [1] , в книге Ф. Маинарди [6] и обзорной статье [7] . Построение новых дробно-дифференциальных моделей, обобщение имеющихся классических моделей, приложение их к моделированию различных вязкоупругих материалов, сравнение с экспериментальными данными, идентификация параметров моделей отражены в

Статья опубликована в открытом доступе по лицензии CC BY 4.0

значительном числе работ, причем многие из них опубликованы в последние годы. Особо стоит отметить активное развитие дробных аналогов классических моделей вязкоупругости [1, 5, 8, 9] , в частности, моделей Максвелла, Фойгта, Кельвина, а также модели Зинера (или модели стандартного вязкоупругого тела), которая применяется в данной статье. Работы [8] и [9] посвящены моделированию процессов ползучести с использованием дробно-дифференциальных обобщений перечисленных выше моделей. Показаны способы построения решений задач ползучести в виде специальных функций, предложены методики идентификации параметров моделей исходя из экспериментальных данных по одноосному растяжению образцов при различных постоянных уровнях нагрузки. В результате поэтапно определяются параметры-константы рассматриваемых моделей.

Применимость дробного аналога модели Зинера для описания поведения вязкоупругих материалов, в частности, демпфирующих полимеров, выявлена достаточно давно; соответствующие результаты представлены, например, в работах [10 –12] . Так, в статьях [11] и [12] исследовано влияние параметров модели на комплексный модуль, а также местоположение и форму так называемого «пика потерь», характеризующего частотный диапазон, в котором наиболее сильно проявляется затухание. Для таких материалов проведено сравнение расчетных данных с экспериментальными. В статье [13] дробная модель Зинера используется для оценки вязкоупругих параметров полимеров, армированных углеродным волокном. Подход к идентификации свойств материала, основанный на наноиндентировании, содержится в [14] . Подчеркивается преимущество дробной модели Зинера относительно классических моделей целочисленного порядка, требующих значительно большего числа параметров для соответствия экспериментальным данным. Представлена методика одновременного отыскания модулей релаксации и податливости в одном эксперименте по индентированию. В работах [15, 16] подобные исследования проводились при учете влияния температуры: в [15] одноосное растяжение с разными постоянными скоростями деформации, в [16] — вибрационное воздействие на различных частотах. В результате по экспериментальным данным удалось определить характеристики вязкоупругого материала.

Дробно-дифференциальные модели также успешно применяются для описания поведения биологических тканей. Например, в работе [17] излагается методика предсказания образования злокачественных опухолей в молочных железах человека. Выделены преимущества дробного аналога модели Зинера по сравнению с классическими моделями для процессов релаксации, где эта модель показала наилучшее соответствие экспериментальным данным. Статья [18] посвящена моделированию процесса релаксации напряжений в легочной ткани свиньи. Выявлено, что дробный аналог модели Зинера лучше аппроксимирует кривые релаксации, по сравнению с дробным аналогом модели Максвелла. Разработанная модель позволяет выявить корреляцию изменения эластичности легочной ткани и признаки некоторых сопутствующих заболеваний.

Наряду с четырехпараметрическим обобщением модели Зинера достаточно широко применяется пятипараметрическая модель Бэгли–Торвика, содержащая уже два параметра порядка дробной производной. Параметрическая идентификация этой модели по имеющимся экспериментальным данным для полимербетона представлена в [19] .

Что касается идентификации характеристик новых неоднородных вязкоупругих материалов, здесь стоит отметить подходы, основанные на акустическом методе, разработанные ранее авторами данной статьи. С их использованием решен ряд обратных задач определения неоднородных механических свойств вязкоупругих материалов [20 –23] и биологических тканей [24, 25] на основе классической модели стандартного вязкоупругого тела (модели Зинера). Данная работа нацелена на развитие проведенных исследований и предложенных подходов для дробно-дифференциального обобщения модели стандартного вязкоупругого тела и на решение соответствующих обратных задач идентификации ее функций-параметров.

• 2.    Общая постановка задачи

Для постановки задачи о колебаниях неоднородного вязкоупругого тела рассмотрим установившиеся колебания с частотой ш упругого тела плотностью р . Тело ограничено поверхностью S = S u U S &, при этом на части S u оно жестко защемлено, а на части S σ нагружено периодически меняющейся во времени нагрузкой P i e ^iωt . Уравнения и граничные условия после отделения временного множителя имеют вид [26] :

(Cijkluk,l) ,j рш ui 0, ui |su   0, Cijkluk,lnj | s^   Pi , где Cijkl — компоненты тензора упругих модулей, ui — компоненты вектора амплитуды перемещений, nj — компоненты единичного вектора внешней нормали к поверхности тела. С использованием принципа соответствия [27] на основе уравнений (1), (2) можно сформулировать постановку задачи об установившихся колебаниях вязкоупругого тела, если заменить компоненты тензора упругих модулей Cijkl компонентами тензора комплексных модулей Gijkl, представляющими собой комплексные функции частоты колебаний и координат.

Для формирования структуры комплексных модулей воспользуемся одномерным определяющим соотношением, записанным при помощи дифференциальных операторов дробного порядка, являющимся обобщением модели стандартного вязкоупругого тела (модели Зинера) [1, 5 –7] :

nD ^a v +ст = EnD ^a e + He.

В (3) входят производные дробного порядка α по времени, введенные согласно определению Римана–Лиувилля [1] :

D^ae =

•■ = -1      ' )     d_Z

dta   dtj Г(1 — a)(t—Z)a , где Г(1 — a) — гамма-функция Эйлера.

Модель (3) является четырехпараметрической, в ее состав входят длительный модуль H , мгновенный модуль E (причем E> H> 0 ), время релаксации n> 0 и параметр дробности a , 0 < a <  1 . Если имеет место установившийся режим колебаний e(t) = E ₀ e i“t, a(t) = ^ ₀ e i“t, то из соотношения (3) можно получить комплексный модуль:

En ^{( iw ) a} + H

^G         ,.(М а + 1 '

который определяет связь между амплитудами напряжений и деформаций как j ₀ = G ( iw ) • е ₀ . Соотношение

^E ijkl ^{n ( iw ) +} H ijkl п (ш) ^а + 1

(5) будем использовать как базовое для введения комплексного модуля общего вида G ijkl = в постановку задачи об установившихся колебаниях вязкоупругого тела .

При рассмотрении материалов вида ФГП компоненты тензоров мгновенных ( E ijkl) и длительных ( H ijkl) модулей являются функциями пространственных координат. Обратная задача заключается в идентификации функций-параметров модели по дополнительной информации о полях смещений, измеренных на некоторой части границы поверхности S σ в заданном частотном диапазоне:

u i | s _CT = .АМ   ^{( i} = 1,2,3),     w e M,w + ].

Сформулированная задача представляет собой нелинейную коэффициентную обратную задачу, решение которой требует применения специальных методов [4] .

З а м е ч а н и е. В данной работе для рассматриваемых объектов из ФГП предлагается методика определения законов изменения мгновенных и длительных модулей из решения соответствующих обратных задач вида (6) . При этом параметры времени релаксации n и дробности α считаются постоянными, и в качестве их могут выступать значения, найденные в эксперименте на ползучесть (см., например, работы [8, 9] ).

• 3.    Исследование комплексного модуля дробно-дифференциального обобщения модели стандартного вязкоупругого тела

Отметим ряд свойств комплексного модуля (5) . Как и для классической модели стандартного вязкоупругого тела, при высоких и низких частотах поведение вязкоупругого материала в рамках модели (3) соответствует упругим материалам, имеющим вещественные модули: lim G(iw) = H , lim G (iw) = E . Для решения прямых задач расчета установившихся колебаний объектов, вяз^ωк ^→ о ⁰ упругое пове^ωд ^→ ен ^∞ ие которых описывается моделью (3) , ввиду их нелинейности применяются различные численные подходы. При этом удобным является разделение вещественных и мнимых частей краевых задач, что позволяет решать их относительно вещественных функций при удвоении числа уравнений и граничных условий.

Итак, отделим вещественную и мнимую часть в комплексном модуле (5) , воспользовавшись формулой Муавра [28] :

(i) ^a = cos(an/2)+isin(an/2).

Тогда комплексный модуль примет вид:

G(iw) = G R^e (iw)+iG ^Im (iw)= J 1 H + J ² E +i J 3 ( E H ) ,

J 1 + J 2        J 1 + J 2

J 1 = 1+ nw ^a cos( an /2) , J ₂ = nw ^a cos( an /2)+ n ² w ^2a , J 3 = nw ^a sin(an/2).

При а = 1 выражение комплексного модуля (7) соответствует модели стандартного вязкоупругого тела:

H + n ² w ² E nw ( E — H ) ^{G ( iw )} = T+nW ^{2 +} i 1+n ² w ² .

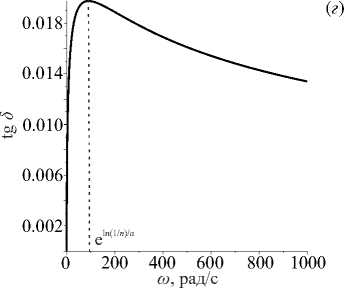
Функции G Re(i w ) и G Im( iw ) обладают рядом свойств. Так, вещественная часть G R ^e ( iw ) положительна и монотонно возрастает, а мнимая G ^Im ( i^ ) положительна и имеет экстремум при w = e in(i/ n ) ^/a . Аналогичные свойства, соответственно, имеют и модуль, и тангенс угла механических потерь tg5 (определяемый отношением мнимой части комплексного модуля к вещественной части). Мнимая часть характеризует затухание в среде, вследствие этого на частотах, находящихся в окрестности значения w = e ^{ln(1/ n ) /a}, затухание колебаний наиболее значительно, то есть сильнее всего проявляются вязкоупругие свойства материала. На рисунке 1 представлены графики вещественной и мнимой частей комплексного модуля (7) , а также его абсолютной величины и тангенса угла механических потерь для следующих значений параметров: длительный модуль H =1.0 ГПа, мгновенный модуль E =1.1 ГПа, время релаксации n = 0.1 с, параметр дробности а = 0.5 .

На рисунке 2 приведены графики тангенса угла механических потерь tg5 , характеризующего затухание в вязкоупругом материале, для нескольких значений параметра α . Видно, что с его уменьшением затухание в материале существенно уменьшается, и материал практически ведет себя как упругий.

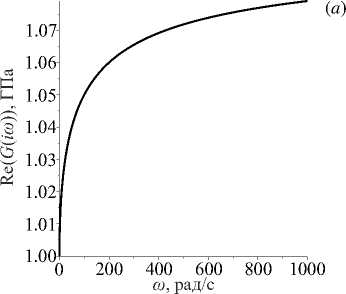
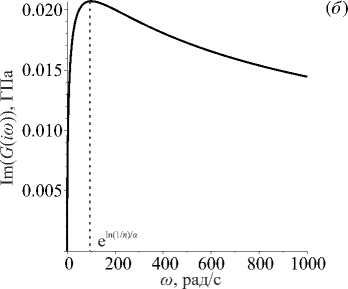
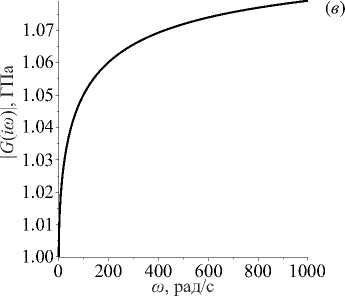
Рис. 1. Графики вещественной ( а ), мнимой ( б ) частей комплексного модуля (7) , а также его абсолютной величины ( в ) и тангенса угла механических потерь ( г )

• 4.    Модельные задачи

Задача 1. Для иллюстрации применения предложенной выше модели рассмотрена задача о продольных колебаниях жестко защемленного на одном конце неоднородного по длине стержня из ФГП под воздействием нагрузки q , приложенной к свободному концу (см. Рис. 3а ). Запишем уравнение колебаний и граничные условия в безразмерном виде:

(^G(€^,iK)w ‘ (€^,K)) - ^{K 2} w(€^,K) = ^{0 ,} w (0 ,k ) = 0 , G(1,iK)w ‘ (1,K) = — q.

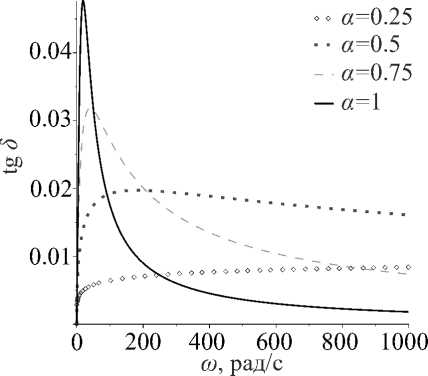
Рис. 2. Графики тангенса угла механических потерь комплексного модуля для различных значений параметра дробности α

Здесь к = wy pl² / H o — безразмерная частота колебаний, где l — длина стержня, Н о характерное значение длительного модуля; w — функция смещения; ξ — безразмерная продольная координата; штрих обозначает производную по ξ .

Задача 2. В другой модельной задаче рассматриваются установившиеся изгибные осесимметричные колебания круглой неоднородной по радиальной координате вязкоупругой пластины в рамках модели Кирхгофа (см. Рис. 3б ). Пластина считается жестко защемленной по контуру. Постановка задачи в обезразмеренном виде в цилиндрической системе координат записывается так:

(G(^,iк)^w ‘‘ («,«)) ‘‘ - (G&ywK^^ - V ( G ( (,iк ) w " ( (,к )) ‘ +

^ξ                                                           (9)

+ v ( G ( ^,iк ) w ‘ ( ^,к )) ‘‘ - к ⁴ ^w ( ^,к ) — kq^ = 0, w (1 ,к ) = w' (1 ,к ) = 0 , w ‘ (0,к) = 0.

Здесь безразмерная частота колебаний к имеет вид: к = w\/ phR / H o (в выражение входят радиус пластины R и ее толщина h ); ξ — безразмерная радиальная координата; ν — коэффициент Пуассона.

Рис. 3. Схемы закрепления и нагружения в модельных задачах: стержня ( а ), круглой пластины ( б )

( a )

q                  ( б )

Расчет колебаний обоих объектов производился численными методами [29] . Для стержня применялся метод пристрелки, для пластины — проекционный метод Галеркина. Вычислительные схемы решения прямых задач подробно описаны в работах [20 –25] .

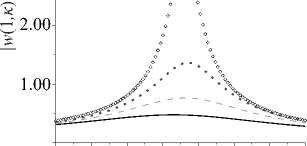
В обеих модельных задачах проведен анализ влияния параметра дробности α на амплитудно-частотные характеристики (АЧХ), использующиеся в качестве дополнительной информации при решении обратных задач, и на значения вязкоупругих резонансов. Результаты расчета АЧХ при а = 0.25, 0.5, 0.75, 1 для обоих рассматриваемых объектов приведены на рисунке 4. Анализ показал, что при увеличении параметра α от 0.1 до 1 значения резонансов и графики АЧХ сдвигаются влево. Также заметно существенное влияние параметра α на затухание (амплитуду в окрестности вязкоупругих резонансов). Видно, что чем меньше α , тем ближе поведение объектов к упругому случаю и тем больше значение амплитуды в околорезонансной области.

Для рассмотренных объектов, согласно постановке (6) , сформулированы обратные задачи идентификации функций мгновенного ( E (£) ) и длительного ( Н (£) ) модулей, входящих в состав комплексного модуля (5) ,

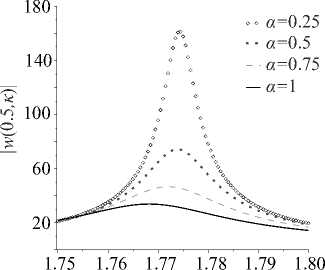
Рис. 4. Анализ влияния величины параметра дробности α на АЧХ в окрестности первого резонанса для стержня ( а ) и круглой пластины ( б )

4.00

( б )

3.00

- a= 0.25 a= 0.5 a= 0.75

— a= 1

2.95     2.97     2.99     3.01

κ

по данным акустического зондирования в выбранной точке £ = £ 0 . Для стержня в качестве дополнительной информации в обратной задаче выступает измеренная на свободном конце ( £ 0 = 1 ) функция смещения, для пластины — значения функции прогиба пластины в некоторой точке внутри пластины (в статье принято £ 0 =0.5 ), при заданном наборе частот. В постановках обратных задач считается, что безразмерные параметры времени релаксации ( τ ) и дробности ( α ) являются постоянными. Для них удобно использовать значения, найденные, например, в эксперименте по исследованию ползучести [8, 9] .

Для построения методики решения обратных задач применен метод линеаризации, построены итерационные процессы. Приведем их общую схему.

Начальное приближение . Для искомых функций H (£) и E(£) выбираются начальные приближения H ⁰ (£) и Е° (£) на основе априорной информации об их положительности и ограниченности. Начальными приближениями могут служить значения (константы), полученные экспериментально (см., например, [8, 9] ).

Этап 1. Для текущих приближений H n (£) и E n (£) с помощью численных методов рассчитываются функции смещения w n (£,к) . Здесь n — номер текущей итерации.

Этап 2. Поправки SH (£), SE (£) определяются из решения интегрального уравнения Фредгольма 1-города:

[ 5H ( £ )+ т ( i^SE^

а ----~ K ^{( £,K} ) ^d£ = f ^{( к} ) ^- wn^ O K ) , ^{к e [ к} 1 ^,к 2 ^] .

1+т ( iK )

Ядро интегрального уравнения (10) имеет вид: для стержня K ( £, к ) = (w'n( £,к )) 2 ; для пластины K ( £,к )= £ (w"( £,K y) 2 + (1/ £ )( w n ( £,к )} ² +2 vw n( £,K ) w 'n (£,к) . В правой части для стержня £ о = 1 .

Решение интегрального уравнения Фредгольма 1-го рода (10) с регулярным ядром является некорректной задачей и требует использования регуляризационных методов [30] . В уравнении (10) производится разделение на вещественную и мнимую части вида (7) , и тогда становится возможной его запиcь относительно поправок SH ( £), SE ( £) в виде системы интегральных уравнений Фредгольма 1-го рода:

где

,, , J^k Re i,M+J3 ( k ) k I ^HW        wk Re w - J^KI-W )

'--------J (к) + W) --------’  - ,^K-------- J , ( k ) _{+ AW} --------,

W)K kw-W^W)  ,, . J1WK WWWK Rew z3(M=----лю+jw----,     ----JSJj----,

K ( f,K ) = K ^Re ( f,K ) + iK I ^H ( f,K ) , W n (M = w Re^ ,K )+ iw^M, f ( k ) = f      if ^Im ( K ) ,

J ₁ ( k ) = 1+TK ^a cos(an/2), J ₂ ( k ) = TK ^a cos( an /2)+ t ² K ^2a , J ₃ ( k ) = TK ^a sin( an /2) .

Этап 3. Поправки, найденные на Этапе 2, используются для вычисления следующих приближений искомых функций:

H ^{n +1} (f) = H ⁿ ( f )+ 6H ( f ) , E ^{n +1} (f) = E ⁿ ( f )+ 6E ( f ) .                      (12)

Затем проверяются условия выхода из итерационного процесса: либо величина функционала невязки вида Ф = max | f ( k ) - w _n ( f ₀ ,K ) l становится меньше некоторого заданного малого числа е ₀ , либо число итераций

К ^ [ К 1 ,К 2]

превышает заданное значение N , либо величина поправок несущественна. Повторение Этапов 1–3 продолжается до выполнения одного из этих условий.

В данной работе произведена доработка Этапа 2 за счет дополнения итерационного процесса проекционным подходом, позволяющим определять поправки к искомым функциям в заданных простых классах функций. В рамках проекционного подхода функции поправок представляются в виде разложений по системам линейно независимых функций вида:

MM

6H ( f ) = X C H ^mW, 6E ( f ) = X CH^f )

m =1                  m =1

Далее, подставив разложения (13) в систему (11) , последнюю можно переписать в виде:

M    1              M1

X C H I ^ _m ( ^ ) z 1 ( ^,K ) df + X C H I ^) ^z 2 ( f^df = f ^Re ( K )

m=1   о

M1

X C H I ^ _m ( f ) z ₃ ( f,K ) df + X C H / ^ _m ( ^ ) z 4 (W d£ = f ^Im ( K ) m =1   о                  h =1 о

w ^R'^{e ( f} o ^,K ⁾ ,

wn^OK ) , ^K ^ [^K 1 ^,K 2 ],

Затем выбирается набор из K безразмерных частот κ i , в которых производится зондирование. В итоге Этап 2 итерационного процесса сводится к решению системы из 2 K линейных алгебраических уравнений относительно 2 M коэффициентов C ff , C H разложений (13) , которую можно записать так:

' м m m m m Re

( C H Z 1 ⁺ C E Z 2 ) = F i ,

H =1

M

X ( C H Z H+ C H Z H) = f    i = 1 ,K,

U=1                                                      (15)

Z H = j^_m (^z ₃ &K ) d£, j = M, о

F i ^Re = f ^Re ( K i) - w Re ( f o ,k ) F^ = f ^IH ( K i) - w ¹™ ( f o ,Kf.

Полученная СЛАУ (15) решается с использованием метода регуляризации А.Н. Тихонова [30] , после этого по формулам (13) определяются искомые поправки к функциям мгновенного и длительного модулей.

• 5.    Вычислительные эксперименты

Для представленных выше подходов проведены вычислительные эксперименты по восстановлению безразмерных функций H (f) и E(f) для обоих рассматриваемых объектов. Параметр, характеризующий время релаксации, полагался равным т = 0.1. Поиск поправок на Этапе 2 производился в классе полиномиальных функций ^j (С) = Cj-1; применялось M = 7 базисных функций в разложении (13). Выход из итерационного процесса осуществлялся по достижению величиной невязки значения, меньшего е = 10-4, или после N = 20 итераций. Вычислительные эксперименты показали, что для идентификации наиболее эффективен выбор частотного диапазона либо в окрестности первого вязкоупругого резонанса, либо между первым и вторым резонансами. Далее на всех рисунках сплошной линией показаны графики искомых функций, пунктиром — начальных приближений, точками — восстановленных функций.

В двух первых примерах производится тестирование разработанного итерационно-проекционного подхода при а = 1 .

Пример 1. Рассмотрен случай восстановления монотонно возрастающих функций H (С) = 0.5 + 0.5^ 2 , Е(С) = 0.6 + 0.6^ 2 в частотном диапазоне [1.45,1.6] в обратной задаче для стержня. Начальные приближения были следующими: H 0 (С) = 0.5 , Е 0 (С) = 0.6 . Потребовалось 6 итераций, при этом относительная погрешность реконструкции не превосходит 3%. На рисунке 5 представлены результаты восстановления.

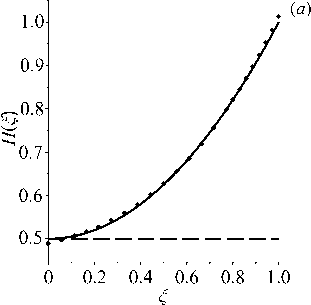
Рис. 5. Результат восстановления монотонно возрастающих функций H ( ^ ) ( а ) и E(^) ( б ) в задаче для стержня в примере 1 при а = 1

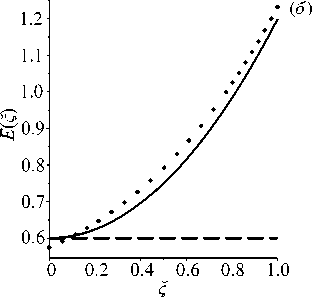
Пример 2. В обратной задаче для пластины восстанавливались монотонно возрастающие функции, такие же как в Примере 1: H (С) = 0.5 + 0.5^ 2 , Е(С) = 0.6 + 0.6С 2 . Начальные приближения имели вид: H 0 (С) = 0.8 , E 0 (С) = 0.9 , частота изменялась в диапазоне [3.5,5.7] . Потребовалось 14 итераций, погрешность восстановления не превосходит 4%. Результат реконструкции приведен на рисунке 6.

В следующих примерах производится восстановление мгновенного и длительного модулей для разных дробных значений параметра α и при различном виде восстанавливаемых функций.

Пример 3. Рассматриваются монотонно убывающие экспоненциальные функции H (^) = 0.5 + 0.5e ^- ^, Е(С) = 0.6 + 0.5e ^— в задаче о стержне при а = 0.5 . Обратная задача решается при начальных приближениях H 0 (€) = 0.85 , E 0 (С) = 0.95 в частотном диапазоне [1.9,3.6] . Для восстановления потребовалось 11 итераций (Рис. 7) ; погрешность не превосходила 1.5%.

Пример 4. Рассмотрены монотонно убывающие экспоненциальные функции H(С) = 1.3 — 0.3e ^, E(e) = 1.5 — 0.35e « в задаче для пластины при а = 0.5 . Начальные приближения имели вид: H ⁰ (С) = 0.75 , E 0 (€) = 0.85 , частота изменялась в диапазоне [3.4,5.6] . Потребовалось 8 итераций (Рис. 8) . Погрешность не превосходит 3%.

Пример 5. Рассматриваются немонотонные функции H(С) = 1.2 — 0.5sin(3£) , Е(С) = 1.3 + 0.5sin(3£ — 3) в задаче о стержне при а = 0.25 . Обратная задача решается при начальных приближениях H ⁰ (С) = 0.9 , Е 0 (С) = 1.0 в частотном диапазоне [1.75,3.95] . Потребовалось 11 итераций (Рис. 9) , погрешность не превосходила 4%.

Пример 6. Рассмотрены немонотонные функции H(С) = 1 — 3(С — 1) 4 , Е(С) = 1.1 — 2.5(С — 1) 4 в задаче для пластины при а = 0.75 . Начальные приближения имели вид: H 0 (С) = 0.9 , Е 0 (С) = 1.0 , частота изменялась в диапазоне [3.3,6.0] . Потребовалось 8 итераций (Рис. 10) . Погрешность не превосходит 4%.

• 6.    Выводы

Для исследования задач об установившихся колебаниях неоднородных вязкоупругих тел, применяемых при акустическом зондировании, представлена модель колебаний, основанная на дробно-дифференциальном обобщении модели стандартного вязкоупругого тела. Изучены свойства модели, проанализировано влияние

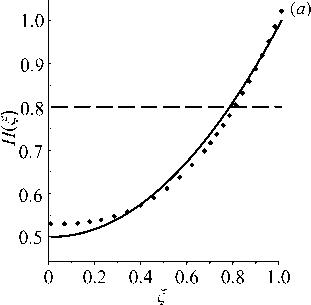
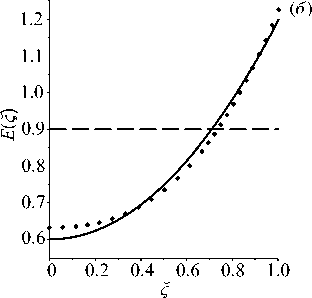
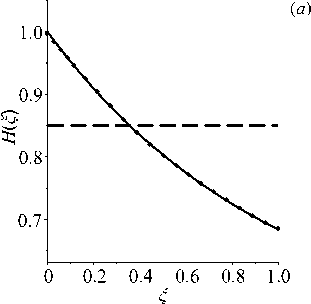
Рис. 6. Результат восстановления монотонно возрастающих функций H ( ^ ) ( а ) и E(^) ( б ) в задаче для пластины в примере 2 при а = 1

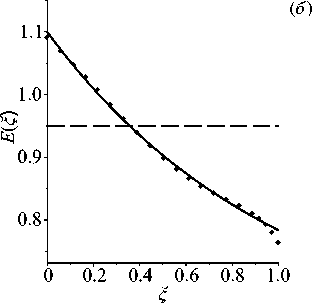
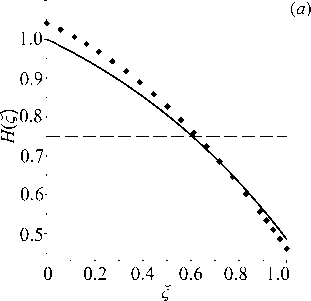
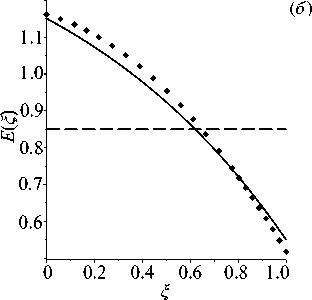
Рис. 8. Результат восстановления экспоненциальных функций H ( ^ ) ( а ) и E(^) ( б ) в задаче для пластины в примере 4 при а = 0 . 5

Рис. 7. Результат восстановления экспоненциальных функций H ( ^ ) ( а ) и E(^) ( б ) в задаче для стержня при а = 0 . 5

ее параметров на комплексный модуль (при использовании дробной производной). Сформулированы общая и частные (модельные) постановки обратных задач идентификации функций-параметров модели для неоднородных материалов типа ФГП для объектов вида стержня и пластины. К решению обратных задач адаптированы разработанные ранее итерационные процессы, дополнительно предложен проекционный подход для определения поправок к искомым функциям.

Проведен представительный набор вычислительных экспериментов по восстановлению законов изменения мгновенного и длительного модулей различного вида — монотонных и немонотонных, характеризующих распределение фаз материалов в структуре ФГП. Восстановление одинаково качественно происходило для различных значений параметра дробности, относительная погрешность при этом не превышала 3–4%. Результаты вычислительных экспериментов свидетельствуют об эффективности предложенного комбинированного подхода, основанного на акустическом методе.

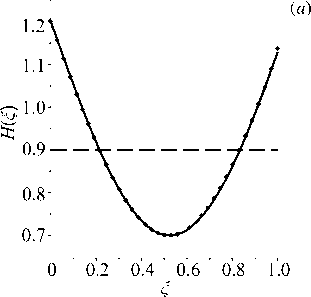
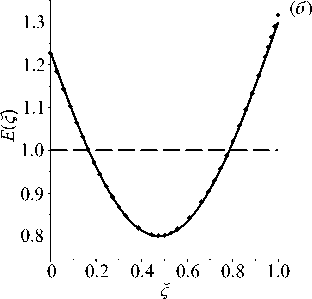
Рис. 9. Результат восстановления немонотонных функций H ( ^ ) ( а ) и E(g) ( б ) в задаче для стержня в примере 5 при а = 0 . 25

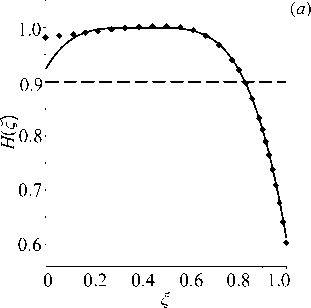
Рис. 10. Результат восстановления немонотонных функций H ( ^ ) ( а ) и E ( ^ ) ( б ) в задаче для пластины в примере 6 при а = 0 . 75

Работа выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации, Государственное задание в области научной деятельности, научный проект № FENW-2023-0012 (Богачев И.В.), и Южного математического института — филиала ВНЦ РАН в г. Владикавказ (Ватульян А.О.).