Об идентификации коэффициента теплообмена в слоистой среде
Бесплатный доступ
Рассматривается вопрос о корректности в пространствах Соболева обратных задач об определении коэффициента теплообмена на границе раздела сред, входящего в условие сопряжения типа неидеального контакта. В цилиндрической пространственной области рассматривается параболическое уравнение второго порядка. Область делится на две подобласти, на общей части границы которых задается условие сопряжения. Коэффициент теплообмена, входящий в условие сопряжения, ищется в виде конечного отрезка ряда с неизвестными коэффициентами Фурье, зависящими от времени. Уравнение дополняется краевыми условиями общего вида и начальными условиями, а также условиями переопределения. Условия переопределения - значения решения в некотором наборе точек, лежащих в пространственной области. При естественных условия гладкости на данные и расположение точек замеров показана локальная по времени теорема существования и единственности решений. Полученное решение является регулярным, т. е. все обобщенные производные, входящие в уравнение, суммируемы с некоторой степенью и уравнение выполняется почти всюду. Метод является конструктивным, и на основе предложенного подхода возможно построение численных методов решения задачи. Доказательство основано на получаемых априорных оценках и теореме о неподвижной точке.
Обратная задача, задача сопряжения, коэффициенттеплопередачи, параболическое уравнение, тепломассоперенос
Короткий адрес: https://sciup.org/147236522
IDR: 147236522 | УДК: 517.95 | DOI: 10.14529/mmph220102
Текст научной статьи Об идентификации коэффициента теплообмена в слоистой среде
Мы исследуем обратные задачи об определении коэффициента теплопередачи, входящего в условие сопряжения. Рассматривается параболическое уравнение вида
Mu = ut - Lu = f ( x, t), (x, t )e Q = G x( 0, T),(1)
n-1
где Lu = annux x + ^ at(x, t) u x +^ a- (x, t) u + a0 (x, t) u , G c Rn - ограниченная цилиндри-nn iji
-
i, j=1
ческая область вида G = Qx(0,l) (Qc Rn-1, dQeC2 ). Пусть r = 5Qx(0,l), S = (0,T)хГ. Положим G1 =Qx(0,a) (a e(0,l)), G2 =Qx(a,l). Уравнение (1) дополняется начальными и крае- выми условиями:
RUs = g, u ( 0, x) = u 0 (x)(x e G ), R u (t, x ',0) = g 0, Ru (t, x', l) = g1$ n-1
,v
i
+
где Ru = u или Ru = ^ a ^ u x
-
i , j = 1
ветственно, R 1 u = u или R 1 u = ux + G \ u , а также условиями сопряжения:
D + du+ _ + —. + du+
B u =--в(u - u ) = g ,---=
SN N dNN du± где ^?( t ’ x)=lim x ^a ±0 annuxn (t ’x, xn) ’u =lim x ^a ±0u (t,x’ xn) • Пусть У;=( y^ a)
dN nn
(i = 1,2, _, r) - некоторый набор точек. К условиям сопряжения мы добавляем условия переопре- деления вида
u(t,yi,Уп)|yn = a+0 = Wi(t)(i = 1^2,^,rb), u(t,y’i,Уп)|yM = a-0 = Vi(t) (i = r0 +1,-,r)•
Задача состоит в нахождении решения уравнения (1), удовлетворяющего условиям (2)-(4) и r неизвестной функции в вида в = ^ pi (t )фi (t, x'), где функции Фi заданы, а функции ai счи-i=1
таются неизвестными. Условия сопряжения (3) совпадают с известными в теории тепломассопе-реноса условия на границе двух сред, когда контакт не является идеальным (см. [1]) Если в ^ гс , мы получим стандартную постановку задачи дифракции (см. [2, 16, гл. 3]), когда условия имеют вид u = и
ди+ дN sо
д и
• д N S о
Обратные задачи вида об определении коэффициента теплопередачи возникают при модели- ровании теплопереноса в теплозащитных материалах и покрытиях, исследовании композитных материалов и т. п. (см. [3-8]). В настоящее время имеется большое количество работ, посвященных численному решения задач типа (1)-(4) в различных постановках, возникающих в приложениях, как правило, ищется коэффициент в , зависящими от времени или наоборот от пространст венных переменных, точки {yt} в (4) чаще всего являются внутренними точками областей Gx , G . В приложениях возникают два случая, в первом из них одна из областей, например, G лежит строго внутри области G и во втором случае рассматривается цилиндрическая область, описанная выше, состоящая из двух или более слоев (см. [7, 8]). Численному решению задачи или близкой к ней посвящены работы [5-12]. В качестве метода почти во всех работах используется сведение обратной задачи к некоторой задаче управления и минимизация соответствующего квадратичного функционала [5, 6, 9-12]. Иногда возникают и задачи об одновременном определении коэффициента, входящего в параболическое уравнение, и коэффициента теплообмена (см. [6]). В этой работе в качестве условий переопределения используются значения замеров температур в точках на границе раздела слоев (как и в условии (4)). Насколько нам известно, теоретических результатов о разрешимости (или единственности решений) задач вида (1)-(4) в литературе не имеется.
В данной работе мы изучаем вопросы корректности задачи (1)-(4), в частности, мы получим теоремы существования и единственности решений (основной результат - теорема 2).
Определения и вспомогательные результаты
В работе мы используем пространства Соболева и Гельдера Wp (G), Wp (Q), Ca (Q) а также их анизотропные варианты Wpr (S), Wpr (Q), Ca,e (Q) (см. определения в [2, 13, 14]). По определению Wp’r (Q) = Wp (0, T; Lp (G)) n Lp (0, T; Wp (G)). Пусть Г - гладкая поверхность размерности n -1 и S = (0,T)хГ. Тогда, соответственно, W,,r (S) = W (J;Lp (Г))пLp (J; W^ (Г)). Под нормой вектора понимаем сумму норм координат. Определение включения dQ g C2 может быть найдено в [2, с. 9]). Пусть (и, v) = J и (x) v(x)dx . Обозначим через B5 (yi) - шар радиуса 5 с цен-G тром в точке yi. Параметр 5 > 0 назовем допустимым, если B5 (yi )ndG = 0, B5 (yi) n B5 (yj ) = 0 для i ^ j . Далее во всех условиях на данные считаем такой параметр фик- сированным.
Введём обозначения: Q^ =( 0,ф)х G, S0 =( 0, T )xQ, S^ =( 0,ф)хО, Г1 =dQx( 0, a ), Г =dQx( a, l), St = (Оф x Pi, Si =( 0, T )хГ i (i = 1,2 ), G5 Ji, (xi), Gf = G5 n Gi (i = 1,2) , Qi = (0, T)x Gi , QT = (0, т)х Gi (i = 1,2). Нам понадобятся весовые пространства Wp,2s ( Q) = {и g Wp,2s ( Q): и"s g Lp ( Q)} с нормой up
WSP2 ( Q )
, TW V)l p dtdx +| T T
J J .sp J J J
V G 0 t G 0 0
| u ( x , t ) - u ( x , t ) | p
- T | 1 + sp
X 1/ p
-dtd T dx + || u|| p
L p (0, T;W p s ( G ))
Вообще говоря, при s < 1/ p это пространство совпадает с Wps,2s (Q), а при s > 1/ p с подпространством {и е Wps,2s (Q): u(0,x) = 0} (см. лемму 1 пункта 3.2.6 в [13]). По аналогии определяем пространства Wps(0,T;Lp(Г)) , Wps,2s(Si) . Положим s0 = 1/2-1/2p , s1 = 1 -1/2p и всюду ниже считаем, что p > n + 2. Доказательство следующей леммы совпадает с приведенным в лемме 2 в [15]). Поэтому мы его опустим.
Лемма 1 Существует постоянная C, не зависящая от фе (0, T ] , такая, что
II V W p 1,2 s 1 ( S f ) +
dv dv
Ws0,2 s 0( s Ф )
- C IM Wp ’2( Q ф ),
- C||v|| 12 , i = 1,2,
Wp2(QI )
II n 2||Ws0,2s0(S-) II V /II 2ф p 0 Wp (S 0
где c = 0 или c = a при i = 1 и c = a или c = l при i = 2, для всех v е Wp’2 (Q1) таких, что v (0, x) = 0. Здесь |v - производная по нормали к Si1.
Лемма 2 Пусть s е(1/p,1). Произведение q • v функций класса WpS,2s (QT ) (т е (0, T]) снова принадлежит Wps,2s ( Q ), а если q е Wps,2s ( QT ) и v е Wps,2s ( Q ) (или v е Wp ,2s (Q)), то справед- ливы соответствующие оценки
II*р,2s (qt)- c01kllWs,2s (qt) IvWp,2s (qt), llqvIWs,2s (qt)- c11klWs,2s (Q) IvWp,2s (q), где постоянные ci не зависят от τ . Множество Qτ в этих утверждениях может быть заменено Qi , Si . В случае если q зависит только одной переменной t, норма q в Wps,2s (QT) в этих неравенствах заменяется на норму q в Wps (0,т).
Доказательство. Доказательство основано на определении нормы и оно повторяет доказательство леммы 1 в [16]. Поэтому мы его опустим.
Оператор L считается эллиптическим, т. е. для некоторой постоянной <50 > 0 выполнено не- равенство
n
^ aij^i^j> 50 ^2 V^ е Bn, V( t, x )е Q, i, j=1
(здесь и далее полагаем, что ani = ain = 0 при i < n ). Приведем условия на данные. Мы предпола- гаем, что ai е Lp (Q)(i = 0,_,n), ay е C(Qk ),^ е Cs0+^0,2s0+2^0 (Sk ),
a ij Sk
е C s 0 + ^ 0 , 2 s o + 2 ^ 0 +8 ( S k ) , ^ k е C s 0 + ^ 0’2 s 0 + 2 e ° ( S 0 ) , i , j = 1,
n , k = 1,2,
где 80 е(0,1/2) - положительный параметр (он может быть как угодно мал) и включения aiA ,аеCs0+80,2s0+280(Sk) означают, что aiA ,ое Cs0+80,2s0+280(Sk) и эти функции допускают
Sk Sk непрерывное продолжение на Sk класса Cs0+80,2s0+280(Sk). При переходе через плоскость xn =a они, вообще говоря, имеют разрывы первого рода.
Дополнительно предположим, что ai е L^ (0,T; WP (Gf))(i = 0,_,n),aij е L„ (0,T; WP (G5k )),i, j = 1,2,_,n, (9)
где k —1,2. Построим функции pi (x)e C°(Rn) такие, что pi(x) — 1 в B5/2(xi) и pi(x) — 0 в Rn \B3d/4(xi) , положим p(x) —^pi(x) (i —1,2,...,r). Считаем, что i
-
2 —
u 0 ( x ) e W p p ( G k ) , g + e U p "2 s 0 ( S 0 ) , g i e W^ k 1 ( S 0 ) , g e W^ 0,2 k 0 ( S i ) ( i — 1,2 ) , (10)
где k0 — s0 (соответственно, k1 — s0 ) в случае условий третьей краевой задачи и k0 — s1 (соответ ственно k — st ) в случае условий Дирихле. Условия согласования при t — 0 записываются в виде:
z x 1 d u + d u n
g (0, x ) — Ru 0 г,—0- — —0-, V 7 01 r d N d N
R + „ -5 М +
B U(\ —
0 d N
—
e ( u + — u 0 ) — g + (0, X ' ) ,
du ± Z X z . ■ Z . „ где -^X (x ') — annu0x (0, x', a ± 0), u± — u0 (x ', a ± 0). Пусть также f e Lp (Q),ann (t,x',a ± 0)e Cs0's0' (\,), Vxpf (t,x) e Lp (Q),
-
V x -V U 0 ( x ) e W p ; p ( G k ) V x p g + e W p 0,2 s 0 ( S 0 ) , V x . ann ( t , x ', a ± 0 ) e W ,2 s 0 ( S 0 5 ) , Ф i e U p , 2 s 0 ( S 0 ) , V x Ф i e W p 0 , 2 s o ( S q ^ ) , i — 1, _ , r , k — 1,2,
где S05 =(0,T)хи.=1 B5 (yt'), положим S^5 =(0,r)xuf=1 B5 (yi'). Нам понадобятся дополнитель- ные условия согласования:
А) если R i u — u ( i — 0,1) и Ru — u , то g i (t , x ’)|a Q— g ( t , x ’, r i ) ( r 0 — 0, r — l ) ; если R i u — u
(i — 0,1) и Ru ^ u , то R ( t , x ’, rt ) g i ( t , x f)| — g ( t , x ’, rt ) ; если R i u ^ u ( i — 0,1 ) и Ru — u , то
Rig (t, x', r) — gi (t, x ')| ; если Ru = u , то B + g — g +(t, x ')| и -g- = дg-, где d^ d^
d g ±
----— a^gx ( t , xa ± 0 ) .
d n nn^xn \ /
Приведем теорему о разрешимости прямой задачи.
Теорема 1. Пусть выполнены условия A), (7)-(14) и Pe Wps0,2 s 0 ( S 0 ) , V x ‘ P e W pS 0,2 s 0 ( S 0 ^ ) .
Тогда для любого т e (0, T ] существует единственное решение u задачи (1)—(3) такое, что u , V x ‘ p u(t , x ) e W p ’2( Q T ) a W p 1,2 ( Q T ) • Если u 0 = 0 , то справедлива оценка
||V x 4 u ( t , x )|| W 1,2 ( Q T ) +||V x ф ( t , x )|| W 1,2 ( Q T ) +1 u Wp2( Q T ) +1 u Wp2( Q^
C 1 d I g ll Wk 0 ,2 k 0 ( S T ) +l I g l Wk 0 ,2 k 0 ( S T ) +l I f II L , ( Q T ) +IIV x 'pAbp (Q T ) +l g +ll Ws 0 ,2 s 0 ( S T )
+ ||V x ’p g + ( t , x ')|| Ws 0 ,2 s 0 ( S T ) +ll g 0I | Wk 0 ,2 k 0 ( S T ) +ll g 1l Wk 2 ,2 k 2 ( S T )), (16)
где постоянная C1 не зависит от т e (0, T) и k0 — s1 или k1 — s1 или k2 — s1 если соответствую щий оператор R или R0 , или R1 определяет условие Дирихле. Если оператор R или R1 или R2 задает условие типа Робина, то k0 — s0 или, соответственно, k1 — s0 или k2 — s0 .
Доказательство теоремы 1. Утверждение о разрешимости задачи (1)–(3) из класса u e W^ ( Q T ) a Wy ( Q T ) вытекает из теоремы 3 [17]. Наша задача – частный случай задачи рассмотренной в этой теореме. Однако, к сожалению у нас есть отличия в условиях гладкости на коэффициент β . Вообще говоря в [17] требуется, чтобы он принадлежал некоторому классу
Гельдера. Однако само утверждение теоремы 3 сформулировано для любого p . В нашем случае условие p > n + 2 гарантирует, как и в случае пространств Гельдера, справедливость соответствующей теоремы о точечных мультипликаторах для пространств Соболева (лемма 2) и соответственно справедливость этой теоремы. Утверждение о дополнительной гладкости решения может быть легко доказано с помощью метода конечных разностей. Фактически, доказательство совпадает с доказательством первой половины теоремы 4 [18, гл. 4, §2, п. 3], где вначале устанавливается дополнительная гладкость решений по касательным переменным. Обоснование того факта, что постоянная C 1 в (16) может быть взята не зависящей от т осуществляется по той же схеме, что и в доказательстве теоремы 2 в [17].
Основные результаты
Приведем дополнительные условия на исходные данные. Пусть Ф(t) - матрица с элементами Ф. = Фj (t, yj) . Мы предполагаем, что u+ (У'j) * u- (У'j ) (i = 1,2,^, r )Jdet Ф|> 51 > 0 Vt e[0, T ].(17)
u+(У'j) = ^(0), ^i(t)eWps(0,T) (i = 1,2,_,r0), u-(yj) = ¥i(0) (i = r +1,...,r),(18)
где 5 - некоторая положительная постоянная. Рассмотрим равенство (12) в точке (0, у j ):
B+ и0 ‘^'-у')-в(0,Уj)(u0+ (Уj)-u-(yj)) = g + (0,yj), в(0,yj) = £А(0)Фi(0,yj).(19)
dN
Положив в0 =(P (0),•••,Pr (0)), F = (F1,^,Fr), получим систему f du + (y') + )//\
Ф (0 Ж = F 0 , F j = - g j + (0, y j ) ( u + ( y j ) - u - ( y j ) ) , j = 1,2,..., r ,
-
V dN7/
которая в силу условия (17) имеет единственное решение в . Положим в = ^z r • в ( 0 ) Ф i ( t , x ' ) , a = ( a 1, ^ , ar ) , a k = P k -P k ( 0 ) , a ( t , x ’) = P ( t , x ’) - P 0 ( t , x ’) . Тогда, чтобы было выполнено (12), необходимо
^uy (x) = M0, x')(u +- u- )(x') + g + (0, x'), ^ (x') = du7 (x'), x'eQ.(2°)
dN dNd
Считая, что условия теоремы 1 выполнены, построим решение w0 задачи сопряжения (1)-(3) на промежутке [0, T], где возьмем функцию Р0 вместо в . Отметим, что в силу условия (15) и леммы 2, в0 e WpS0,2s0 (S0), VxP0 e WpS0,2s0 (S05) и таким образом, условия теоремы 1 на коэффи циент в выполнены. Условия (17), (18) и включение w0 e Wp’2 (Qk )c Ca/2,a
( Q k )
( a < 2 - ( n + 2 ) / p , k = 1,2) гарантируют существование постоянных т 0 > 0, 5 2 > 0 таких, что Ж 7) - w - ( t , У 7| > 5 2 > 0 ( i < Г 0 ), l ^ i ( t ) - w + ( t , y ' j )l > 5 2 > 0 V t e [ 0, r 0 ], ( i > Г 0 ).
Сделаем замену u = v + w 0 в (1)-(4). Функция v есть решение обратной задачи
Mv = vt -
+
— - P 0 ( v + - v ") = a ( v +
■ Lv = 0, BvS = 0, v |f=0 = 0,
-a , + -a d v + .
- v ) + a ( w 0 - w 0 )» ”^ = "
—
d v z, . ,,
—, ( t , x ) e S 0 ,
v + ( t , y 'j ) = Vi ( t ) = ^ i ( t ) - w + ( t , y 'j ) ( i < r 0 ), v ( t , y j ) = ^ i( t ) = ^ i ( t ) - W 0 ( t , у 'j ) ( i > r 0 ).
Сформулируем основной результат.
Теорема 2. Пусть выполнены условия A), (7)-(11), (13)-(15), (17), (18), (2°) . Тогда на
неко-
тором промежутке [ 0, т 0 ] существует единственное решение u задачи (1)-(4) такое, что u e W p ’2 ( QT° ) ( i = 1,2 ) , P i ( t ) e W p0 ( 0, т 0 ) ( i = 1,2, ^ , r ) , причем V x , ^ u ( x ) e W p ’2 ( Q i 0 )( i = 1,2 ) .
Доказательство. Достаточно доказать разрешимость вспомогательной задачи (22)-(24). Построим интегральное уравнение для нахождения вектор-функции а . Фиксируя функцию а и применяя теорему 1 к задаче (22)-(23), мы построим отображение а ^ v ( а ). Возьмем точку y , ' gQ и функцию ф , ( i < r ) . Умножая уравнение (22) на ф , , имеем
Mw = wt - Lw = [ ^ , L ] v = f 0, w = ^ i v , wt = o = 0, (25)
где [^ L ] v = 9 i Lv - L ( p v ) = - 2 j a ik v x^^ - jj a ik V V ix^ - j a ^ v . Равенства (25) можно пе -
-
l, k=1 l, k=1
реписать в виде w - ann (t,x) Wxnxn = j ajw x +^^х.+ aow+fo = fP
-
i, j=1 Ji
Отметим, что ann > 0 для всех t,x . Имеем, что f 1 , V x . f e L p ( Q ) . В силу теорем вложения, f 1 ( t , x',X n ) e C a ( Q ; Lp ( ( 0, t ) x ( 0, l ) ) ) с a < 1 - ( n - 1 ) / p , после может быть изменения на множестве меры ноль (см. соотношения (3.1)-(3.3), (3.5), (3.6), следствие 4.3 в [19] и включение (5.71) в
[20]). Рассмотрим уравнения wit ( t, xn )-ann ( t, Ум xn ) wixnXn = f1 (t, y, ', xn ) (i = 1,2,^, ro ) , wit (t, xn )-ann (t, y, ', xn ) wXnXn = f1 (t, У?, xn ) (i = ro + 1,—, r ) .
Дополним уравнения (27), (28) начальными и краевыми условиями
w(0,x„) = 0,wJ n=^(t),wA =0,г i\ , n) , ilxn = a+0 /, i xn = a+5 , 0v 7 wi(0, xn ) = 0, w,^ = a-0 =^i( t ), wilxn = a -5 = 0 i > r0- Решение wt задачи (27), (29) (или (28), (30) соответственно) существует и единственно [2]. В случае если v,а есть решение задачи (22)-(24), имеем, что w, (t,xn) = ф,v(t,y',xn ) . Перепишем условие сопряжения (23) в виде a+n v+„(t, x') - в(v+ - v - )(t, x') = a( v+ - v - )(t, x') + a( w+ - w- )(t, x ), Рассмотрим это условие в точке (t,y') и используя (24), получим a+n(t,у, ')v+n (t,y') -в(v+ - v-)(t,yi') = a(v+ -v-)(t,y,')) + a(w+ - w-)(t,y,')), i = 1,2,—,r,,(32) a-n(t, у, *) v-n(t, у, ')-A)(v + - v-)(t, у, ) = a(v+- v")(t,y,,)) + a(w+- w-)(t,y,')), i = r0 +1,—,r• Искомая система для нахождения координат вектора а имеет вид a(t, у, ')=(a™(t, уi') wixn (t,a)- Ai(v + - v- )(t, у i')+ av"(t,y, '))/(^.(t) + (w+ - w-)(t,y,')) = F, i= 1,2,-,Г0,(34) a(t, y i') =(a-(t, yi')wixn (t,a) - e0(v + - v")(t, y,')- av + (t, yi'))/(-^i(t)+(w+ - w- )(t, y,))=F,i=r0+1’-’r • Отметим, что в силу (21) знаменатели в этих равенствах строго отделены от нуля на промежутке [0, T0]. Здесь v - решение задачи сопряжения (22)-(23), а функции w, - решения задач (27), (29) и (27), (30) соответственно. Она также может быть переписана в виде а=ф-1 F (a)=r (a),(36) где координаты вектора F определены равенствами (34), (35). Отметим, что лемма 2 гарантирует оценку IIФ-1FWwp? (0,т) < cllFWpo (0,т). (37) Покажем, что оператор R (а) является сжимающим в некотором шаре Bro = («е Wp0 (0,т) :|аWs>(0,т) < R0} и переводит его в себя. Возьмем а = 0. Тогда в силе единственности решений задачи сопряжения (22)-(23) v = v(а) = 0, в этом случае вектор F (0) запи- шется в виде Fi (0) = ann ('’Уг ’)®ixn ('’a)/Wt) + (W0 - W)(t,yi OX i = 1,2,..„r0, Fi(0) = a-n('’y ')^xn ('’a)/(-¥i(t) + (w+ - W)(t’yDX i = rO + 1,...,r’ где ωi решения задач (27), (29) или (28), (30) равны нулю. Положим R = 2||ф-1 F(0)||^s0^о^ соответственно, где правые части в (27) и (28) . Получим оценки, считая, что а е Bn и т< т0 . Из теоремы 1 вытекает оценка II vWP2ет) +vWp2 (ет) +lvx ^v (', x )l W1,2 ( qt ) +|vx ^v(', x )| W1,2 ( Qt ) < col kv+-v-) +а( w+ - w- )||^,2so (ST ) + ||Vx '^(а( v + - v - ) + а( w+ - w- ))('’x D)! |WS0,2so (ST ))’ (38) где постоянная c не зависит от τ . Воспользовавшись леммой 2, получим, что первое слагаемое J0 в правой части здесь оценивается через J0 < c1 lidWp0,2s0(st)(lv+ -v llwp0,2s0(sT)+||w+ -w0 IIWs0,2s0(So))• Второе слагаемое J1 оценивается через J1 < c2(|Vxа|Iwso,2s0(ST5) (ll(v+— v — )|lws0’2so(ST) +|k4- w- )(t,x')|Iwso-2SO(s0)) + IIаW^s0’2so(S0T)(|Vx^(v + - v")|W^0,2so(ST) +Ivxф(w+ - w-)(t,x')|Wso,2so(S))• В силу леммы 2 имеем оценку IIаW-s02s0(SO ) +Hvxа1 Wso,2so(S^ ) < C3 ]E Iki 11^ ^1фilWsO’2 so (So )+llVxфilWs0’2 so (So5)]< c4 аWps0( 0,t) ’ где постоянная c4 , равно как и постоянные c0 - c3 , не зависит от т . Далее, у нас имеет место оценка II(v +-v )lIw^o,2so(ST) +IIVx'ф(v +-v )|IWsO’2so(ST)< c5T1/2 ^1 MWP’2( QT) +1 MWP’2( QT) +Iv x ^v ( t ’x )| W1,2( QT) +Iv x ^ ( t ’x )| W1,2( QT) j ’ (42) которая была получена в доказательстве теоремы 3 в [17] (см. неравенства (50)–(52)). Приведем краткое доказательство. Оценим первое слагаемое в (42). Второе оценивается точно так же. Имеем - ±1 Ip Wp0(0,t) = T v4p d' + T T1 v±(‘)-M±(^"pddT< T(s'"so)P lv±1 Ip 0 's0 P 00 I' - ^1+s0IP Wps1(0,T) . Отсюда вытекает, что IIv±1 kp(Q; Wp0(0,t))< T1/2Iv±1 kp(Q; Wp1(0,t По лемме 1 правая часть оценивается через Ст1/2 (IMW1,2(qt) + |MIIW1,2(qt)). Таким образом, имеем неравенство: IIV + 1Lpp (nWs0 (0,т )) +lM ILp (n;Ws° (0,т)) (MW1,2( qt ) + | MW1,2( q2)). (45) Оценим нормы ||v±|L(0,т;W1-1/p (Q))• Например, для функции v+ имеем, что IIM +lL (0,т;W1-1/p (Q)) < c6MLp(0,7;Wp (GT)) < c71Ml\m, , IMW2 , <c8?/21MW.2(qt).(46) p\ p \ 7 J \ J Lp (Q2) Wp (Q2) \ / Здесь мы воспользовались теоремой о следах [13, теорема 4.7, с. 412] и соответствующей оценкой IIV + |W-Vp(Q)< cjM +|W. (g2), интерполяционным неравенством IIV +lW(g2)< cIV +l 1 ^)IV+ W2(g2) и неравенством ||v +|Lp(0,t) IIV ILp(0,т;Ji)Mp (Q)) <CgT1/2!MIWp-2(q) Таким образом, справедливо неравенство (42). Из (38)-(42) вытекает неравенство IIVWp'2(QT) +1MWp'2(QT) +|Vx-^(t,x)|W1,2(q) + |Vx.^(t,x)|W1,2(qt) < c10T ■1/2ЙWs°(0,7) MWp-2(qt)+1 MWp-2(Q2 ) ■ Vx^V(t,x)W1,2(qt) +||Vx.^(t,x)W1,2(QT) +c10 I Wil Ws (0,t)(|k w+ - w0 )(t, x ')|^,2S0 (SQ ) +||Vx '^(W+ -W0)(t, x ')||Ws0,2 S0 (5())). (48) Выбрав т1 такое, что c10R0T12 = 1/2 , из (48) получим, что при т < т2 = min(71,7°) имеет ме- сто неравенство IIVWp’2(QT ) +1 MWp2 (QT ) +|Vx^V (t,x)W1,2(QT ) +|Vx^V(t, x)W1,2(QT ) < 2Сю IWIIWs0(0,T) (||(W+ -w-)(t,xr)||WS0,2S0(So) +||Vx'^(w+ -w-)(t,x')||WS0,2S0(^)). (49) Пусть W =(ai1,ai2,^,air)eBR) (i = 1,2) и vi - соответствующие решения задачи (22), (23), r c функциями ai = ^wi-j-Ф j (i = 1,2) вместо a . Имеет место оценка (49), где в правой части стоят j=1 соответствующие нормы ||aillWs0 (0,т). Тогда разности v1 - v2 = ю, у = a1 - a2 есть решение за дачи +со + Mv = rot -Lrn = 0,B^s = 0,dt=0 = 0,—- = ——, dNd дю+ „ , + -. (a, + a2) + - у ++ V1 - V2 ) +Y(wo- w0 ). (51) -^- -P°(to-Ю ) =-------(d -® ) + — (M + V2 - Пусть у = a1 - a2. Задача (50), (51) имеет тот же вид, что и задача (22), (23), поэтому при т< т2 имеет место та же оценка (49), которая запишется в виде IIdWp’2(QT ) +1dWp’2(QT ) + ||Vx^d(t,x)W1,2(QT ) +|Vx^d(t,x)W1,2(QT ) < 2ciolIFI IWp°(o,t)(2(v+ + - -\ + - + V2 — V — V2 ) + Wo — Wo + Wpo,2 s0( so) Vx Ф(1(v1+ + V2 - V1 - v2 ) + W+ - Wo ) )• W.' so( So) Из оценок (42), записанных для функций v1, v2 , и (52) вытекает неравенство ®Wp’2(QT) +1® Wp2(Qt) + ||Vxф(°(t,x)|Wl^Q} + ||vx-ф®(t,x)|W1,2 (QT) -c11l H Wso (o,T) (lW+ - W-1 W;o.2 s o(s0) + |v x Ф( W+ - W- ) IWWso(s0)), где постоянная c11 не зависит от т . Пусть w/ (j = 1,2) - решения задач (27), (29) и (27), (30) c новыми правыми частями, где вместо v стоят функции vi , и wo = ф®. Тогда разности ki = W1 - w2 есть решения задач kit - ann (t, Уь xn ) kixnxn = X aij®^ +iLaia>Zi + ao®° +[фi, L ]® x '=У = fi (t, У’, xn ),(54) i, j=1 k.l = o,kA = o,kA „ =o (i - r0),(55) i It=o ’ ilxn = a ’ i\xn = a+S V oP v7 kA = o,kA = o,kA = o (i > r ).(56) i It=o ’ i\xn = a ’ l'xn = a-S V o/ x7 Из известных свойств параболических задач (см., например, [2]) имеем оценку ro r XIIkillWJ’2((o,t)x(a, a + S)) +X^'kiWp’2((o,t)x(a - S, a)) -f r) oГ ) c13 XIIfi'ILp((o,t)x(a,a + S)) + X_^Ilfi’ILp((o,t)x(a -S,a)) • Пусть, например, i - ro . Имеем IIf(t, yi, xn ) LP ((o,T)x( a, a + S)) - c141Ifi'(t,x ) Ws (fi; Lp (( o,t)x( a, a + S))) = J,s >(n -1)/p, (58) в силу теорем вложения (см. следствие 4.3 и соотношения (3.1)–(3.12) в [19]). Далее используем неравенства, вытекающие из соответствующих интерполяционных теорем (см. следствие 4.3 и соотношение (3.7) в [19]). J-c151Ifi-(t,x)|W1 (fi;Lp ((o,t) x (a,a + S))) IIfi'(t,x)IWp!(fi;Lp ((o,t) x (a,a + S))),26 -1= s. (59) Ввиду замечания 5.3 (c) в [19] норма в последнем пространстве может быть определена как II fiV-1( fi; L, (( o,t)x( a, a + S))) = , suP |(?i ,ф)|, 17P+17q =1, P V PVV 7 V Ф^Уд(fi;Lq((o,T)x(a,a+S)))' 1 где скобки обозначают продолжение скалярного произведения в L2 до отношения двойственности между соответствующими пространствами. Исходя из определения fi и условий на коэффи- циенты имеем I f'i\Wp-1(fi; Lp (( o,t)x( a, a + S))) - c16 fl® Lp ( o,t; WP (G1 ))+l® Lp ( o,t; WP (G2 )))- C17T1/2 fl ® Wp.2 (QT ) + Ы Wp-2 (Q2T)^, (60) где постоянная c1 не зависит от т . Последняя оценка получается, если мы применим интерполяционное неравенство и ( л г II1/2 II 1|1/2 У ( 0тWp(Gj)< ( 0Т wp (Mlp ( 0,r. Lp ( Q^ и оценку ML^(0,T;Lp (Q.)) < T|VJ|£(q г* L (G )) , вытекающую из формулы Ньютона-Лейбница, а затем оценим полученные нормы через норму в Wp’2 (QT). Оценки (59), (60) влекут, что Ifi(t• xi,x,)|Lp((0,г)х(a,a + 5))<c1T " ' lvX»™(‘,x)Wp.2,e;) + IIvx^t.x)|W 1.2,Q) + (Itilwp\Q)+1^Wp2(Q^9(^WtiQx)+1 ^!wp’2(QtFe- p X ^2 Г PP где c19 - постоянная не зависящая от т . Как вытекает из неравенства (53), неравенство (61) можно переписать в виде If(t,X,xn)| 1^((0,т)х (а,а + 5)) < С20т(1"У)/21If I Wp0(о.т), i < ro- Очевидно, что такая же оценка имеет место и в случае i > r^ . Из (57), (62) вытекает неравен ство r0 r В частности, отсюда вытекает оценка r §К(t, а )Iwp0 (0т) < Ст " И4° (0,т)- Оценим ||^(ax) - R(а2)||^08о^ . Из (37) вытекает оценка Рассмотрим первое слагаемое в координате Fi (а1) - Fi (а2) . Пусть, например, i < r0 . Оно за- писывается в виде J1 = а+ (t,yi')(toiXn- toiXn)(t, а) / (yi(t)+(w+- w")(t,yf)) В силу леммы 2 и неравенства (63) имеем IJ1IWs0(0т) <С. h>Zn - ^£,1^)0(, . cT !“■" а21 Wp(' ■ , где все постоянные не зависят от т , в1 - положительная постоянная. Рассмотрим второе слагае- мое J2 = -в0 (w+-w")(t,yi') / (Wi(t)+(w+ -w")(t,Ух D). В силу леммы 2 имеем IIJ2II ^S0(0, r) < c25 § ||(to+ -®")(t, У oil ^S0(O,r)-p ;=1 p v 2 / Справедливы очевидные оценки (лемма 1, (53) и теоремы вложения (см. [19])) Iw±(t,yi ’>1 W^0(0,r) < c1 kw±(t,x')lWp(Q; Wp0 (0,t))< С26 IIvxkw (t,x’)|L^(q;wp0(0,t))+Ikw(t,x')lLp(q; Wp0(0,t))< 1/2 С27т IVX ^w(t, X)W1,2(Q ) + I^w(t, X ’)|W1,2(QT ) < c29т1/2 ||a1 - a2IIwjo(0,т), 11/2 С28т где i > r0 и k = 1 в случае функции го и k = 2 и i < r0 в случае функции го . Таким образом, справедлива оценка IIJ2IIwso(0,Т) < С30тШ1 la1 -a2Wp0(0,т) • для некоторой не зависящей от τ постоянной c . Оценка последней разности J3 =(a1Vf (t, x) - a2v2- (t, Xi.)) / (y (t) + (w+ - w- )(t, xi (0))) получается аналогично, и имеем, что найдутся постоянные в3> 0 и с8 такие, что IIJз1 W^0(0,т)< с31твU1 - a2Wp0(0,т) . Окончательная оценка, как вытекает из (65), (66), (67) имеет вид IR(a)-R(a2)|^(0,т)<т" a1 -a2W(0,т), где показатель в минимальный из полученных в доказательстве и постоянная с31 не зависит от т . Возьмем в качестве т0 число со свойством т0 < т2 , СуГ^0 < 1/2 . В этом случае оператор R переводит шар BR в себя и является в нем сжимающим. Следовательно, уравнение (36) имеет решение a е Wps0 (0,т0). Найдем решение задачи сопряжения v . Покажем, что мы нашли решение нашей обратной задачи. Достаточно показать, что у нас выполнены условия переопределения (24). Мы имеем равенства (32), (33) и равенства (34), (35), откуда вытекает, что a+n(t, у, D wxn (t, a)- Р0(v+ - v - )(t, у, D=a(^i(t)- v-)(t, yt D)+a(w+ - w-)(t, yt D, при i < r0 и при i > r0 имеем a+n (t, yi) Wixn (t,a) - Mv+ - v- )(t, yi D = a( v+ (t, y^-yi( t)) + a( w+ - w- )(t, yiD Вычитая (32) и (69), соответственно, (33) и (70), получим a+n(t,yi')(v+n (t,y')-wxn (t,a)) = a(v + -^i(t)) = a(v + (t,у, ')-w(t,a)), i = 1,2,^,r0, a-n (t, У')(v- (t, У,') - wtxn (t, a)) = a(^t(t) - v" ) = a(wt, a) - v" )» i = r0 +1—,M, Функция w0i = фiv удовлетворяет уравнению (26). Возьмем в этом уравнении х’= у' и вычтем его из равенства (27) при i< r0 и из (28) при i > r0 . Получим равенство ( wit ( t, Xn )-w0 it (t, yi', Xn ))-ann (t, yt', Xn )( wtxnxn - w0ixnxn (t, Xi, Xn )) = 0(73) где i = 1,2,^,r. Функции wi = wi (t,Xn)-w0i (t,Xi,Xn) удовлетворяют уравнению (73), начальному условию wil^ = 0 и в силу (71), (72) граничным условиям ann (t, Xi ) wtXn (t, a ) = -awi (t, a ), wi (t, a + ^) = 0, i = 1,2, —, r0, a-n (t, yt') wiX„ (t, a ) = awt (t, a ), wi (t, a - ^) = 0 i = r0 +1,—, r. В силу единственности решений смешанной начально-краевой задачи wi (t, Xn ) = w0i (t, yi ’, Xn ). Следовательно, выполнены равенства w0i (t, yi ’, a + 0) = yi для всех i< r0 и w0i (t, yi', a - 0) = yi для всех i > r0 . Поскольку локально по времени задача сводится к уравнению со сжимающим оператором, то утверждение о единственности решений здесь очевидно. Замечание. Все результаты справедливы и в случае более сложной задачи когда вместо одного условия сопряжения мы рассматриваем несколько условий, скажем в точках xn = ^,l2 ,...,lm и неизвестными являются несколько коэффициентов теплопередачи. На каждом из сечений xn = l, в некотором наборе точек у нас, как и ранее, заданы значения решения в качестве условий переопределения. Соответствующие условия на данные легко формулируются.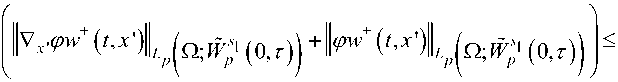
Список литературы Об идентификации коэффициента теплообмена в слоистой среде
- Baehr, H.D. Heat and Mass Transfer / H.D. Baehr, K. Stephan. - Berlin Heidelberg: SpringerVerlag, 2006. - 688 p.
- Ладыженская, О.А. Линейные и квазилинейные уравнения параболического типа / О.А. Ладыженская, Н.Н. Уральцева, В.А. Солонников. - Москва: Наука, 1967. - 736 с.
- Алифанов, О.М. Обратные задачи в исследовании сложного теплообмена / О.М. Алифа-нов, Е.А. Артюхин, А.В. Ненарокомов. - Москва: Янус-К, 2009. - 299 с.
- Ткаченко, В.Н. Математическое моделирование, идентификация и управление технологическими процессами тепловой обработки материалов / В.Н. Ткаченко. - Киев: Наукова думка, 2008. - 243 с.
- Huang, C. An inverse problem of simultaneously estimating contact conductance and heat transfer coefficient of exhaust gases between engine's exhaust valve and seat / C. Huang, T. Ju // International journal for numerical methods in engineering. - 1995. - Vol. 38, Iss. 5. - P. 735-754.
- Loulou, T., An inverse heat conduction problem with heat flux measurements / T. Loulou, E. Scott // International Journal for Numerical Methods in Engineering. - 2006. - Vol. 67, Iss. 11. -С. 1587-1616.
- Identification of Contact Failures in Multi-Layered Composites / L.A. Abreu, H.R.B. Orlande, C.P. Naveira-Cotta et al. Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Vol. 2: 31st Computers and Information in Engineering Conference, Parts A and B. Washington, DC, USA. August 28-31, 2011. -P. 479-487.
- A Comparison of two inverse problem techniques for the identification of contact failures in multi-layered composites / L.A.S. Abreu, M.J. Colaco, C.J.S. Alves et al. // 22nd International Congress of Mechanical Engineering (COBEM 2013), November 3-7, 2013, Ribeirao Preto, SP, Brazil. - С. 54225432.
- Artyukhin, E.A. Reconstruction of thermal contact resistance from the solution of the inverse heat conduction problem / E.A. Artyukhin, A.V. Nenarokomov // Journal of Engineering Physics. -1984. - Т. 46, № 4. - С. 677-681.
- Drenchev, L.B. Inverse heat conduction problems and application to estimate of heat parameters in 2-D experiments / L.B. Drenchev, J. Sobczak // Proc. Int. Conf. High Temperature Capillarity, Cracow, Poland, 29 June - 2 July 1997. - Krakow: Foundry Research Institute, 1998. - С. 355-361.
- Zhuo, L. Reconstruction of the Heat Transfer Coefficient at the Interface of a Bi-Material / L. Zhuo, D. Lesnic, S. Meng // Inverse Problems in Science and Engineering. - 2020. - Vol. 28, Iss. 3. -С.374-401.
- К решению нестационарных нелинейных граничных обратных задач теплопроводности / Ю.М. Мацевитый, А.О. Костиков, Н.А. Сафонов, В.В. Ганчин // Проблемы машиностроения. -2017. - Т. 20, № 4. - С. 15-23.
- Трибель, Х. Теория интерполяции. Функциональные пространства. Дифференциальные операторы / Х. Трибель. - М.: Мир, 1980. - 664 с.
- Denk, R. Optimal Lp-Lq-Estimates for Parabolic Boundary Value Problems with Inhomogene-ous Data / R. Denk, M. Hieber, J. Pruss // Mathematische Zeitschrift. - 2007. - Vol. 257, Iss. 1. -P. 193-224.
- Belonogov, V.A. On Solvability of Some Classes of Transmission Problems in a Cylindrical Space Domain / V.A. Belonogov, S.G. Pyatkov // Сибирские электронные математические известия. - 2021. - Т. 18, № 1. - C. 176-206.
- Вержбицкий, М.А. O некоторых обратных задачах об определении граничных режимов / М.А. Вержбицкий, С.Г. Пятков // Математические заметки СВФУ. - 2016. - Т. 23, вып. 2. - C. 3-18.
- Белоногов, В.А. О разрешимости задач сопряжения с условиями типа неидеального контакта / В.А. Белоногов, С.Г. Пятков // Известия вузов. Математика. - 2020. - № 7. - C. 18-32.
- Михайлов, В.П. Дифференциальные уравнения в частных производных / В.П. Михайлов. - М.: Наука, 1976. - 391 с.
- Amann, H. Compact Embeddings of Vector-Valued Sobolev and Besov Spaces / H. Amann // Glasnik matematicki. - 2000. - Vol. 35(55). - p. 161-177.
- Grisvard, P. Équations différentielles abstraites / P. Grisvard // Annales scientifiques de l'École Normale Supérieure, Série 4. - 1969. - Vol. 2, no. 3. - P. 311-395.


