Об индикаторах структурной дифференциации населения по доходу

Дифференциации населения по денежным доходам, по заработной плате, по имуществу и т. д. посвящено большое количество работ [Айвазян C.А, 2012; Бутаева К.О., 2016; Бобков В. Н. и Колмаков И. Б., 2017; Аникин В.А. и Тихонова Н.Е., 2014; Гречаный С.А. и Родин В.А., 2008; Громыко Г.Л. и Матюхина И.Н., 2004; Лившиц В.Н., 2018; Лукьянова А.Л., 2013; Шевяков А.Ю. и Кирута А.Я. 2009; Fellman J. 2012; Giorgi G., 1990;

Rohde N.,2009; и др.]. Важное место среди различного рода вопросов, связанных с анализом неравенством распределения различных денежных активов, занимает проблема его количественной оценки. На практике применяются различные показатели дифференциации: коэффициент Джини, коэффициент фондов, коэффициент Рейнбоу, индексы Тейла, Аткинсона, Херфиналя-Хиршмана, Гувера и др. Особое место среди количественных показателей неравенства занимает коэффициент Джини, который остается одним из основных индикаторов неравенства.

В этой связи уместно сказать об относительно недавней дискуссии на страницах журнала «Вопросы статистики» по поводу применении коэффициента Джини в экономикостатистических исследованиях [Громыко Г.Л. и Матюхина И.Н., 2015; Глущенко К.П., 2015]. В ходе этой дискуссии было отмечено, в частности, что в опубликованном в 1990 г. обзоре говорится о более чем 700 работах по проблематике коэффициента Джини и смежным вопросам [Giorgi G., 1990]. В ходе дискуссии было высказано предположение о том, что за следующие 25 лет число таких работ выросло еще больше, вероятно перевалив за тысячу [Глущенко К.П., 2015].

При анализе статистической информации часто возникают вопросы о точности и достоверности значений коэффициентов (индикаторов), отражающих уровни дифференциации населениях, т. к. их официальные оценки в ряде случаев представляются спорными, несоответствующими фактическому уровню. Так, согласно данным Федеральной службы государственной статистики в 2012 г. значение коэффициента Джини для Москвы было на уровне 0,417 [Росстат, 2020]. С другой стороны, по мнению многих специалистов реальное значение этого коэффициента находилось в 2012 г. в интервале 0,6–0,7 [Шмерлинг Д.С., 2011]. Актуальность работ по анализу дифференциации населения по доходам в России определяется, в частности, тем, что вопрос об уровне неравенства в настоящее время остается одним из самых дискуссионных [Суворов А.В., Сухорукова Г.М., Иванов В.Н., Болдов О.Н. и Моисеева Т.А., 2014]. Важное место среди работ этого направления занимает совершенствование количественных методов анализа структурного неравенства.

Индикаторы неравенства и структурная дифференциация

В дальнейшем для определенности будем говорить о неравенстве распределения доходов. Примем следующие обозначения: x величина денежного дохода (размерность – рубль); y доля населения с доходами не более x в общей численности населения; z доля совокупных доходов населения, доходы которых не более x . С формальной точки зрения для вычисления коэффициента Джини и других количественных показателей неравенства используются функции распределения населения по доходу y — F(x) и функция Лоренца z = L(у), параметры которых определяются на основе решения соответствующих задач аппроксимации.

С формальной точки зрения можно выделить две основные задачи, которые необходимо решить для определения числовых значений индикаторов дифференциации населения по доходам на основе использования статистической информации.

Задача 1 связана с построением функции распределения населения по доходу у = F ( x ) на основе известной информации о распределении населения по величине среднемесячных денежных доходов. В этом случае используется таблица ( x_k , у_к ), где x_k — значение дохода; y доля населения, имеющего денежный доход в месяц не выше уровня x , k 1, 2, …., M . Обычно предполагается также, что известно значение среднедушевого дохода Ц . После построения монотонно возрастающей функции распределения у = F ( x ) на основе решения задачи аппроксимации строятся заданные на отрезке 0, 1 соответствующие ей обратная функция x = ф( у ) и функция Лоренца ^y

L(У ) = - Гф( t)dt .                                  (1)

Ц о

Отметим, что при построении функции y = F(x) используется следующая формула для вычисления среднего значения дохода всего населения:

ц = J ф( t)dt .                                     (2)

о

Задача 2 связана с построением функции Лоренца z — L(у) на основе известной информации о распределении общего объема денежных доходов по некоторым группам населения. На практике эта информация обычно приводится для децильных или квинтильных групп (10- и 20-процентным группам населения, ранжированного по доходу). В этом случае функция Лоренца строится в конечном итоге на основе табличных данных (ys; zs), где у5— кумулятивная доля населения, т. е. доля населения, имеющего доход не выше значения x = ф(у$); zs - доля дохода населения, имеющего доход не выше значения x -ф(у5) в общем доходе всего населения; s =0, 1, 2, .„., N. Здесь у0 =0, z0 =0, yN =1, zN = 1. После построения функции Лоренца z = L(у) на основе использования методов аппроксимации строится функция распределения населения по доходу. Эта процедура осуществляется в два этапа. На первом строится функция, обратная функции распределения:, где x = ф(У), ф(У) = dL • dy

На втором этапе строится функция распределения населения по доходу у = F ( x ), где

F ( x ) = ф ¹ ( x ).

Задачи 1 и 2 взаимосвязаны. В дальнейшем для определенности будем считать, что информация о распределении общего объема денежных средств по N группам населения, ранжированного по доходу, задана табличной функцией Лоренца (ук; zk), где Ук = к / N, zk lL(yk) , к =0, 1, 2, ...., N . При построении этой табличной функции Лоренца исходной информацией служат статистические данные о средних значениях дохода в N группах населения: [1к,где к = 1, 2, ...., N . В частности, если N = 10 или N = 5, то предполагаются заданными значения средних доходов в 10-процентных (децильных) или 20-процентных (квинтильных) группах соответственно. Выпишем формулы для вычисления некоторых индикаторов дифференциации населения по доходам, которые будут использованы ниже для анализа структурного неравенства.

Коэффициент Джини (коэффициент концентрации дохода) по определению равен

KG = 1-2j L ( у ) dy .                        (4)

Используя метод трапеций для приближенного вычисления определенного интеграла, из формулы (4) получаем

N -¹ 1 э ^KG = — >-² zav •

где z_m- среднее значение N -1 значений функции Лоренца z_x , z ₂,_, z_{N ч}:

1 N -1

z ¹ V av N -111

Обобщенный коэффициент фондов

m

^GFn / m —

n

11- n    А^10- n "*"..."*■ №о

Р, 1+^+... + m_m

.

Этот коэффициент, предложенный в работе [Лебедев В.В. и Лебедев К.В., 2019], равен отношению значений средних доходов двух крайних групп населения. Первая группа состоит из n децильных групп населения с самыми высокими доходами, а вторая - из m децильных групп с самыми низкими доходами. Если m = n = 1, то использование формулы (6) дает значение децильного коэффициента фондов: GF_m ⁼ Eio / Ei. Если m — n — 2 , то обобщенный коэффициент фондов равен значению квинтильного коэффициента фондов (отношение значений средних доходов двух 10-процентных групп с наибольшими и наименьшими доходами): GF _2/2 = (ц₉ +Цю)/ (Ei + E2) • Если же m = 4, а n = 1, то обобщенный коэффициент фондов равен значению коэффициента Пальмы KP , умноженному на 4. Это связано с тем, что коэффициент, предложенный Пальмой, может быть вычислен по формуле

KP = ------^Eio------ .

E 1 + e ₂ +ц з + E 4

Поэтому

GF₄ =---- ^4E10-----= 4 KP .

E1 "*" E 2 "*" E 3 "*" E 4

Обобщенный коэффициент фондов можно вычислить, используя функцию Лоренца:

_{GJ? =} m 1- L (1- n /10) ⁿ / ^m   n    L ( m /10)

.

Коэффициенты расслоения . Если доходы x в некоторой группе населения D удовлетворяют условию ф( m /10)< x <ф( n /10), где m и n целые числа, m + 2< n <10, то коэффициенты

и

SX n / m =

(p ( n /10)

( m /10)

SF n / m =

E n

^E m +1

будем называть соответственно коэффициентами расслоения первого и второго рода населения, принадлежащего группе D .

Коэффициент расслоения второго рода применяется в случае, когда построение функции, обратной функции распределения, затруднено. В частном случае m = 0, n = 10 коэффициент расслоения второго рода равен децильному коэффициенту фондов.

Коэффициент расслоения первого рода в частном случае m = 1, n = 9 равен децильному коэффициенту дифференциации ф(0,9)/ ф(0,1):

SX 9/1 =

Ф(0,9) ф(0,1)

Сделаем важное замечание. Децильный коэффициент дифференциации, который иногда обозначают «P90/P10» и иногда называют коэффициентом Рейнобоу, обычно трактуется как отношение минимального дохода 10-процентной группы населения с самыми высокими доходами к максимальному доходу 10-процентной группы населения с самыми низкими доходами [Салмина А., 2019; Гречаный С.А. и Родин В.А., 2008]. Однако этот коэффициент (в случае непрерывной монотонно возрастающей функции распределения населения по доходу) равен также отношению значений наибольшего и наименьшего дохода в 80-процентной группе населения, в которую не входят первая и десятая децильные группы. Поэтому можно считать, что при использовании децильного коэффициента дифференциации «P90/P10» все население фактически разделяется на три группы в пропорции 10-80-10, а рассматриваемый коэффициент дифференциации равен коэффициенту расслоения первого рода средней (80-процентной) группы населения.

Наряду с децильным коэффициентом дифференциации «P90/P10», применяются также децильный коэффициент дифференциации «P90/P50» и децильный коэффициент дифференциации «P50/P10», которые вычисляются по формулам ф(0,9)/ф(0,5) и ф(0,5)/ф(0,1) соответственно [Салмина А., 2019]. В силу формулы (10) имеем:

ф(0,9) / ф(0,5) = SX 9/₅ , ф(0,5) / ф(0,1) = SX 5/1 .

Поэтому при использовании рассматриваемых децильных коэффициентов дифференциации все население фактически разделяется на четыре группы A, B, C и D в пропорции 10-40-40-10, а децильные коэффициенты дифференциации «P90/P50» и «P50/P10» равны коэффициентам расслоения первого рода 40-процентных групп B и C соответственно.

Коэффициент Пальмы. Наряду с часто применяемыми при анализе структурной дифференциации населения по доходам разбиениями можно (и нужно) рассматривать и другие варианты разбиений, если доступные статистические данные позволяют это делать. В последнее десятилетие развитие этого направление анализа дифференциации населения связано с именем Пальмы, предложившим относительно недавно индекс (8), который равен отношению общих доходов 10% самого богатого к общим доходам 40% самого бедного населения [Palma G., 2013; Cobham A. and A. Sumner A., 2013]. Таким образом, при построении индекса (8) Пальма фактически использовал разбиение всего населения на три группы A , B и C в пропорции 40-50-10. При обосновании такого разбиения Пальма опирался на гипотезу, которую он сформулировал на основе анализа реальных статистических данных. Согласно этой гипотезе средний доход в группе B , составляющей 50 процентов населения, находится на уровне, близком среднему доходу всего населения; поэтому общий доход в группе B составляет примерно половину суммарного дохода всего населения. Таким образом, индекс Пальмы (8) отражает распределение половины суммарного дохода всего населения между 40 процентами бедной части населения и 10 процентами населения с высокими доходами.

Несмотря на свою относительную новизну коэффициент Пальмы применяется в настоящее время в научных публикациях [Золотухина Л.А., Тихоненко Г.М. и Фридман Г.М., 2015, Салмина А., 2019; Лебедев В.В. и Лебедев К.В., 2019] и ряде статистических обзоров [Доклад, 2016]. Анализ статистической информации свидетельствует о том, что гипотеза Пальмы о получении 50 процентов суммарного дохода группой B справедлива для распределения заработной платы во многих отраслях РФ: значения средних заработков в средних группах (при разбиении работников в пропорции 40-50-10) для всех организаций РФ, а также для подсистем «Научные исследования и разработки» и «Образование» мало отличаются от соответствующих средних значений всех работников [Лебедев В.В., Лебедев К.В., Соляник Г. Ю. и Тюпикова, 2019].

Отметим также, что анализ статистической информации свидетельствует о высокой корреляции индекса Пальмы, являющегося одним из показателей структурной дифференциации населения по доходам, с коэффициентом Джини, являющегося интегральным показателем неравенства. Для углубления анализа структурной дифференциации мы считаем целесообразным не ограничиваться упомянутыми выше разбиениями населения и использовать другие варианты в зависимости от особенностей статистических данных о распределении населения по доходу.

О подходах к построению функции Лоренца

При построении кривой Лоренца для анализа конкретной статистической информации о неравенстве населения по доходу используются различные одно- двух и даже трехпараметрические функции. О практической значимости исследований по данной Международный электронный журнал. Устойчивое развитие: наука и практика [Электронный ресурс] / гл. ред. А.Е. Петров. – Дубна : 2008-2020. – ISSN 2076-1163. – Режим доступа: тематике можно судить по работе [Пахомов Е.В., 2012], в которой кривая Лоренца используется для оценивания коэффициент регресса по России в целом и по федеральным округам на основе данных Росстата, а на основе выполненного анализа обоснован перечень направлений необходимых исследований, направленных на улучшение качества прогнозирования страховых взносов во внебюджетные фонды.

Один из наиболее распространенных подходов к построению функции Лоренца опирается на гипотезу о том, что двухпараметрическое логнормальное распределение адекватно отражает распределение населения России по доходу [Айвазян С.А, 2012; Колмаков Г.Б., 2004; Гречаный С.А. и Родин В. А., 2008; Методика, 2017; Золотухина Л.А., Тихоненко Г.М. и Фридман Г.М., 2015]. Однако существуют и альтернативные варианты. Так, в упомянутой выше работе [Пахомов Е.В., 2012] кривая Лоренца аппроксимируется дугой окружности

( y+ a)²+( z -1-a)² = R ², (12)

где R2—2a2+2a + 1, re [0,1], z <1. Уравнение построенной кривой Лоренца имеет один параметр α0, а соответствующее значение коэффициента Джини вычисляется по формуле

KG = R ²

Приведем несколько других примеров представления функции Лоренца, используя принятые выше обозначения:

L (y ) = yee(У-1),(13)

L ( У ) = У “ eв( УЧ),(14)

L ( у ) = 1-(1- у )0,(15)

L (У ) = У1+m .(16)

Эти функции использованы при анализе дифференциации населения по доходу в работах [Kakwani N. and Podder N., 1973, 1976], [Rasche R., Gaffney J., Koo A. and Obst N., 1980], [Шмерлинг Д.С., 2011] соответственно. В работе [Sharif H. and Chikayoshi S., 2011] построена трехпараметрическая функция Лоренца

L ( У ) = У ^а е^^У ") [ [1-(1- У )⁶],                            (17)

где а > 0, в > 0, 0 < 0 < 1. Частными случаями этой функции являются функции Лоренца (13)

- (15). В работе [Sharif H., Chikayoshi S., 2011] доказано, что коэффициент Джини для функции (17) вычисляется по формуле

KG = 1-2 -- B (5, 0 + 1) + ^(-1) j [ B (5, j + 1)- B (5,0 + j + 1)] ,

_ 5                    j=1                                            _ где 5=1+a, B(u, v)— бета-функция.

В работе [Нартикоев А.Р. и Пересецкий А.А., 2019] при моделировании распределения населения России по доходам на основе квартальных микроданных доходов домохозяйств за период 2003-2015 гг. применяется четырехпараметрическое обобщенное бета-распределение второго типа (GB2).

В работах [Лебедев В.В. и Лебедев К.В., 2017] функция распределения населения по доходу аппроксимируется трехпараметрической логистической функцией

₌ a 1-exp[⁽ x o -x )/ h ^] a + exp[( x₀ — x )/ h ]

В работах [Лебедев В.B. и Лебедев К.B.,  2018,  2019] функция Лоренца аппроксимируется однопараметрической функцией

L(У) = y + g(1 - У) ln(l - У), которая во многих случаях адекватно отражает эмпирические данные. Коэффициент Джини для функции (19) вычисляется по формуле

KG = g /2.

Продолжающиеся до сих пор поиски адекватного представления функции Лоренца связаны с тем, что оценки неравенства населения на основе их использования существенно зависят от допущений о распределении, допущений о функциональной форме и методологий оценки [Sharif H., Chikayoshi Saeki, 2011].

Практические результаты

В таблице 1 приведены значения табличных функций Лоренца для Москвы и Калужской обл.: (yk; zm), где k= 0,1, . „, 10, m= 1, 2, построенных на основе известных значений заработной платы в децильных группах работников организаций m . Верхний индекс m 1 соответствует данным г. Москва, а индекс m 2 - Калужской обл. Значения zm вычислены на основании данных Федеральной службы государственной статистики [Росстат, 2020] по следующему алгоритму:

ц = 0,1^р _к ; у o =O; z o =O; X_к =p к /ц; Z k = Z k -1 ⁺^ к /1°; Ук = к /10; к =1,2,.10.

к =1

Табличные функции Лоренца для Москвы и Калужской обл. ( y_k ; z_k ), где к = 0, 1, ..., 10, m 1, 2, аппроксимировались функцией (19). Использование метода наименьших квадратов привело к следующим результатам: индекс Джини (коэффициент Джини, умноженный на 100) для Москвы составил 43,4, а для Калужской обл. – 33,7. При этом средняя абсолютная ошибка аппроксимации составила для Москвы 8,2% а для Калужской обл. – 6,12%. Если вычислять индекс Джини по формуле Брауна, то его значение для Москвы составит 42,9, а для Калужской обл. – 33,5. Различия с вычисленными значениями индекса Джини на основании использования функции (19) для Москвы чуть более 1%, а для Калужской обл. 0,45%.

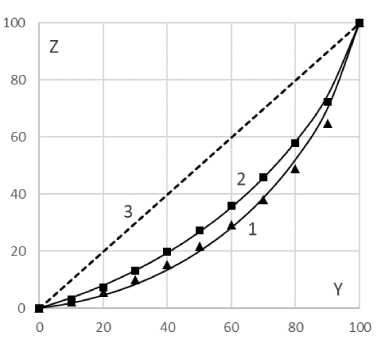
Приведенные результаты говорят о хорошем соответствии функции (19) эмпирическим функциям Лоренца. Иллюстрацией этого вывода служит рис. 1, на котором построены кривые Лоренца (19) для распределения заработной платы работников организаций г. Москвы (линия 1) и Калужской обл. (линия 2) в апреле 2019 г. Здесь же построены табличные точки, отмеченные для Москвы треугольниками, а для Калужской обл. – квадратами. Линия 3 на рис. 1 – линия идеального равенства.

Таблица 1. Табличные функции Лоренца для Москвы и Калужской обл.
k	0	1	2	3	4	5	6	7	8	9	10
н к		12,2	18,2	23,0	27,4	31,2	35,8	41,5	48,7	60,0	113,3
н 2		20,6	33,2	42,5	51,3	60,7	71,6	86,3	102,9	153,6	337,8
y k (%)	0	10	20	30	40	50	60	70	80	90	100
z к (%)	0	2,1	5,6	10,0	15,4	21,7	29,1	38,1	48,8	64,8	100
z k (%)	0	3,0	7,4	13,0	19,6	27,2	35,9	46,0	57,9	72,4	100
Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Рис. 1. Кривые Лоренца для распределения заработной платы работников организаций г.

Москвы (линия 1) и Калужской обл. (линия 2)

Таблица 2. Показатели структурной дифференциации работников организаций Москвы и Калужской обл. по заработной плате

	μ	IG	GF 1/1	GF 2/2	μ A	μ B	IG A	IG B	SF 5/1	SF 10/6
Москва	96,0	42,9	16,4	9,1	41,7	150,4	19,6	31,9	2,9	4,7
Калужская
обл.	41,1	33,5	9,3	5,7	22,4	59,8	17,6	23,2	2,6	3,2

Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Перейдем теперь к вопросу о структурной дифференциации. В таблице 2 приведены значения индекса Джини ( IG ), децильного и квинтильного коэффициентов фондов ( GF и GF ) для Москвы и Калужской обл. Эти традиционные показатели свидетельствуют о том, что дифференциация работников Москвы по заработной плате выше, чем в Калужской обл. Используемая информация позволяет углубить анализ. Для этого разобьем всех работников организаций каждого из рассматриваемых субъектов РФ на две равные половины А и В . Первые пять децильных групп всей совокупности работников превратились в квинтильные (20-процентные) группы работников первой половины всех работников ( A ), а вторые пять децильных групп – в квинтильные (20-процентные) группы второй половины работников ( B ).

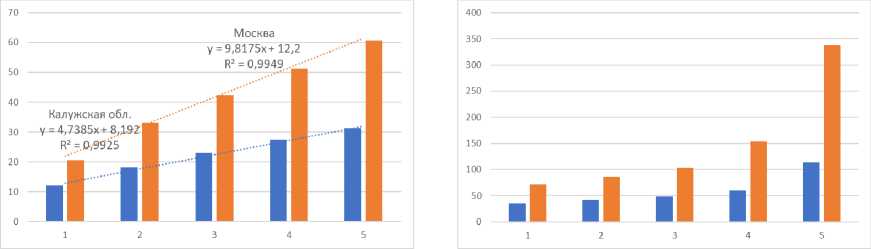
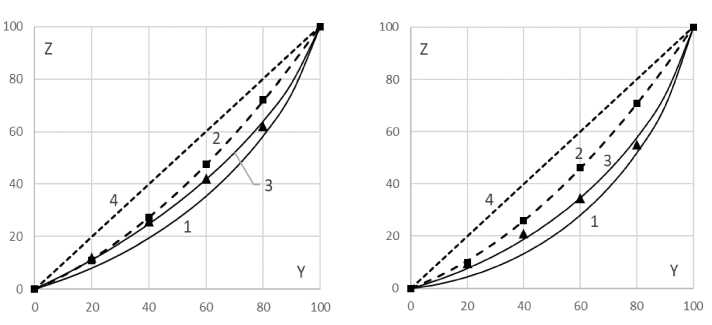
Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Рис. 2. Средняя заработная плата в 20-процентных группах работников организаций Калужской обл. и г. Москвы в апреле 2019 г. (слева – для половины работников этих субъектов РФ с наименьшими заработками, справа – для второй половины этих субъектов)

На рис. 2 приведены две диаграммы, которые отражают средние значения заработной платы в группах А (слева) и В (справа). По оси абсцисс этих диаграмм отложены значения номера квинтильной группы. Для каждой квинтильной группы левый столбик соответствует Калужской обл., а правый – Москве. Как видим, распределение работников с меньшими заработками в обоих субъектах мало отличается от линейного: на левой диаграмме приведены соответствующие уравнения трендов и значения коэффициента детерминации, которые близки к единице.

Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Рис. 3. Кривые Лоренца для распределения заработной платы различных групп работников организаций Калужской обл. (слева) и г. Москвы (справа)

Из сказанного следует, что распределение работников групп А обоих субъектов по заработной плате соответствует равномерному (прямоугольному) распределению, и поэтому соответствующая функция Лоренца задается квадратичной функцией

L ( У ) = У 1- g (1- У ) . (22)

Этой функции Лоренца соответствует коэффициент Джини KG = g /3. Согласно выполненным расчетам, значения коэффициента Джини для распределения работников с меньшими заработками (для группы А ), полученные для обоих субъектов методом наименьших квадратов при использовании функции (22) и методом трапеций (по формуле Брауна), различаются незначительно.

На рис. 3 построены кривые Лоренца для распределения заработной платы различных групп работников организаций г. Москвы (справа) и Калужской обл. (слева) в апреле 2019 г. Здесь линии 1 – кривые Лоренца для всех работников рассматриваемых субъектов, линии 2 – для работников с заработками ниже медианного значения (для группы А), линия 3 – для работников с заработками выше медианного значения (для группы В), линия 4 - линия идеального равенства. Функции Лоренца для всех работников рассматриваемых субъектов и для работников с заработками выше медианного значения аппроксимировались функцией (20), а для работников с заработками ниже медианного значения – функцией (22).

Изложенный подход к вычислению коэффициента Джини для работников организация, разделенных на две группы А и В в пропорции 50-50, был применен для анализа структурной дифференциации по заработной плате работников организаций Центрального федерального округа. Как показали расчеты, усиление дифференциации работников каждой группы сопровождается увеличением общего коэффициента Джини. Сказанное иллюстрируется на рис. 4. Здесь на плоскости построены точки с координатами ( IG, IG_a ) и ( IG, IG_b ) для каждого субъекта ЦФО. 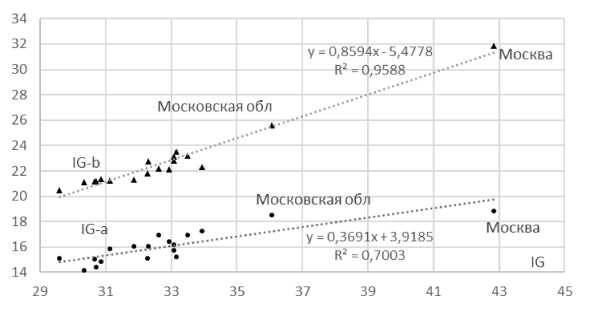Эти две последовательности точек образуют на плоскости два множества IG a и IG b , каждое из которых состоит из 18 точек. На рис. 4 видим, что две пары точек выделяются особо. Это точки, соответствующие Москве и Московской обл. В этих субъектах значения коэффициента Джини как для обеих 50-процентных групп, так и для всех работников выше, чем в любом другом субъект ЦФО.

Отметим, что приведенные результаты опровергают распространенный миф о «зажравшихся москвичах»: значения средней заработной платы в апреле 2019 г. у 50% работников организаций Москвы (группа А, где заработки ниже медианного значения) составляли 41,7 тысяч рублей, а в Московской обл. 29,3 тысяч рублей, что находится на уровне средних заработков работников организаций в других субъектах РФ.

Изложенный подход к определению значений коэффициента Джини в двух равных по численности группах работников позволяет выполнить формальное сопоставление различных субъектов РФ по степени дифференциации работников организаций по зарплате. Для интерпретации результатов количественной оценки структурной дифференциации

Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Рис. 4. Связь региональных индексов Джини работников организаций ЦФО, получающих заработную плату ниже (IG-a) и выше (IG-b) медианного значения, с общим региональным индексом Джини удобно использовать терминологию векторной алгебры. Фактически все, кто занимается вопросами анализа неравенства населения по доходу, имеют дело с векторами, но на этом не заостряют внимание [Лившиц В.Н., 2018].

Напомним, что в качестве исходной информации для каждого субъекта мы использовали данные Федеральной службы государственной статистики о средних значениях заработной платы работников 10 равных по численности (децильных) групп. То есть начальная информация была задана 10-мерным вектором. Для сравнения уровней неравенства различных субъектов непосредственно использовать этот вектор затруднительно; поэтому возникает задача о построении вектора меньшей размерности, который адекватно отражает реальную ситуацию. На основании заданного 10-мерного вектора строится некоторое множество показателей неравенства: индекс Джини, коэффициенты фондов и т.д. Проблема осложняется тем, что многие частные показатели неравенства, такие как квинтильный коэффициент фондов, индекс Пальмы, индекс Кузнеца и др., жестко связаны с коэффициентом Джини, и поэтому последний остается в течение многих лет основным используемым на практике индикатором неравенства. В результате для оценки неравенства используется скалярная величина (индекс Джини), хотя давно существует понимание того, что неравенство следует измерять вектором.

Несмотря на то, что между построенными выше индексами Джини для групп работников А и В и общим индексом Джини работников обеих групп существует корреляция (см. рис. 4), мы предлагаем для оценки структурного неравенства населения использовать трехмерный вектор, координатами которого служат значения индексов Джини для всех работников, а также для двух групп работников, разделенных медианным значением заработной платы: VSD = ( IG, Ю_А, IG_B ).

Покажем, как «работает» этот вектор. На рис. 5 на плоскости XY построены 16 точек ( IG s , IG s ), где s = 1, 2, .., 16, координаты которых равны значениям второй и третьей координат вектора VSD = ( IG , Ю_д , IG_B ), т.е. значениям индекса Джини в группах работников А и В всех субъектов ЦФО, кроме Москвы и Московской обл. Построенная плоскость разделена на четыре части прямыми x = 15,7 и у = 22 (15,7 и 22 — средние значения индекса Джини в шестнадцати субъектах для работников групп А и В соответственно). Эти прямые разделяют все субъекты на 4 группы. В первую входят Воронежская, Калужская, Липецкая, Смоленская, Тульская, Тверская и Ярославская области.

В этих субъектах дифференциация работников выше среднего значения в обеих 50процентных группах работников. Сюда же следует отнести Москву и Московскую область. Вторая группа состоит из двух субъектов: Владимирской и Рязанской областей. Здесь выше среднего дифференциация работников, чей заработок ниже медианного значения, а во второй половине работников дифференциация ниже среднего уровня. Третья «группа» представлена одним субъектом: в Костромской области выше среднего дифференциация работников, чей заработок выше медианного значения, а во второй половине работников дифференциация ниже среднего уровня. И, наконец, четвертая группа состоит из шести субъектов: Белгородcкая, Брянская, Ивановская, Курская, Орловская и Тамбовская области. В этих субъектах значения индексов Джини для обеих 50-процентных групп работников ниже средних значений.

На основании анализа результатов выполненных расчетов можно сделать следующие выводы:

• 1)    существенный «вклад» в дифференциацию работников по заработной плате вносит разрыв в оплате труда работников 9-ой и (особенно) 10-ой децильных групп с остальными работниками;

• 2)    при средней заработной плате в Москве в 2019 г. на уровне 96 тысяч рублей средняя заработная плата одной половины москвичей была равна 41,7 тысяч рублей (на уровне средней заработной платы в Калужской области), а другой половины – 150,4 тысяч рублей (разница более чем в три раза);

  Y (IG-b)

  
  

  Костромская обл, ]

  
  

  Воронежская обл.

  
  

  Калужская обл.

  
  

  Липецкая обл.

  
  

  Тульская обл.

  Смоленская обл,

  
  

  Тверская обл.

  
  

  " Ярославская обл.

  
  

Брянская обл.

Курская обл.

Рязанская обл. Владимирская

Ивановская обл."

Орловская обл. Тамбовская об!л.

Белгородская обл.

X (IG-a)

14                 15                 16                 17                 18

Источник: расчеты авторов по данным ФСГС [Росстат, 2020]

Рис. 5. Использование вектора VSD = ( IG , IG A , IG_B ) для сопоставления неравенства по заработной плате в субъектах ЦФО

• 3)    при средней заработной плате в Калужской области на уровне 42 тысяч рублей средняя заработная плата одной половины работников этого региона была равна 22,4 тысячи рублей, а другой половины – 59,8 тысяч рублей (разница почти в три раза);

• 4)    показатели дифференциации половины работников, получающих заработную плату ниже медианного значения, в обоих субъектах различаются не существенно, вследствие чего различия соответствующих кривых Лоренца (линий 2 на рис. 3) также не существенны;

• 5)    дифференциация работников с заработками ниже медианного значения в обоих субъектах существенно ниже, чем у второй половины работников (так, индекс Джини для Москвы в группе А составляет 19,6, а в группе В – 31,9; эти же показатели для Калужской области равны соответственно 17,6 и 23,2).

Заключение

Продолжающиеся до сих пор поиски адекватного представления функции Лоренца связаны с тем, что оценки неравенства населения на основе их использования существенно зависят от допущений о распределении, допущений о функциональной форме и применяемой методологии оценки. Проблема оценки уровня дифференциации населения но доходу осложняется тем, что многие частные показатели неравенства, такие как квинтильный коэффициент фондов, индекс Пальма, индекс Кузнеца и др., жестко связаны с коэффициентом Джини, и поэтому последний остается в течение многих лет основным используемым на практике индикатором неравенства. В результате для оценки неравенства фактически используется скалярная величина (индекс Джини), хотя давно существует понимание того, что характеристикой неравенства является вектор.

Для совершенствования количественной оценки структурной дифференциации населения по доходам в работе использован подход, в котором все население региона, ранжированное по доходу, разбивается на несколько групп. Конкретно при апробации этого подхода основное внимание уделено разбиению работников организаций субъектов ЦФО РФ на две равные по численности части А и В . На основании анализа статистических данных установлено, что распределение по заработной плате работников, получающих заработную плату ниже медианного уровня, соответствует равномерному (прямоугольному) распределению, и поэтому соответствующая кривая Лоренца является параболой. Обоснован вывод о том, что распределение по заработной плате работников, получающих заработную плату выше медианного уровня, с высокой степенью точности аппроксимируется двухпараметрическим экспоненциальным распределением. Это позволило выполнить количественные оценки значений индекса Джини не только для распределений по заработной плате всех работников организаций субъекта, но также и для двух равных по численности их частей А и В . Для оценки структурного неравенства населения предложено использовать трехмерный вектор, координатами которого служат значения индексов Джини для всех работников, а также для двух групп А и В работников, разделенных медианным значением заработной платы: VSD = (IG, ЮА, IGB). Использованный подход позволил разделить 18 субъектов ЦФО РФ на 4 группы, каждая из которых имеет свои особенности структурной дифференциации работников организаций по заработной плате. Выполненные предварительные расчеты дают основание для вывода о том, что разработанная методика может применяться для анализа структурной дифференциации по денежному доходу не только населения регионов, но и работников различных отраслей.