Об интерполяции гравитационного поля Земли
Автор: Кузнецов А. А., Фукин И. И., Вафин К. М., Завьялова Н. А., Негодяев С. С.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Механика
Статья в выпуске: 4 (60) т.15, 2023 года.
Бесплатный доступ
Для прецизионного прогнозирования орбит в околоземном пространстве необходимо вычисление тяготения Земли с высокой точностью. Расчет гравитационного потенциала и его градиента может быть наиболее затратной стадией интегрирования уравнений движения. В работе исследована возможность интерполяции гравитационного потенциала с целью ускорения построения траекторий. В качестве интерполянтов рассматривались трикубический сплайн и интерполянт на узлах Чебышева - Лиссажу. Авторы оценили ошибки интерполяции и необходимый объем информации для хранения интерполянтов.
Гравитационный потенциал земли, трикубический сплайн, интерполяция чебышева - лиссажу
Короткий адрес: https://sciup.org/142239996
IDR: 142239996 | УДК: 531.5
Текст научной статьи Об интерполяции гравитационного поля Земли
«Московский физико-технический институт (национальный исследовательский университет)», 2023
Наиболее распространенными моделями гравитационного поля Земли являются модели EGM96 [13], EGM2008 [14] или GRACE [15]. Эти и большинство других моделей [16] предполагают представление гравитационного потенциала U в виде усеченного ряда Гаусса [17], [18]:
N
п
U — Ц У О ” У Р пт (sin у) \СТ1т^) cos(mA) + Snm(t) sin(mA) ] . п =0 m =0
Под (г , у, A) следует понимать геоцентрические координаты точки пространства с радиус-вектором г, под t — время, под циа- гравитационный параметр и экваториальный радиус модели, под N — степень модели, а под Рпт(х) — нормированные присоединенные полиномы Лежандра, связанные с присоединенными полиномами Лежандра Рпт(х) следующим образом:
Р ы - N р м N - / ( п - т )!(2 п + 1)(2 - ^ 0т ! гпт \Х> — J ’пт гптЬ*Ъ -‘•пт — \ / , м •
( п + т )!
Здесь 50т — символ Кронекера. Функции Спт (t) и Sпm(t) в (1) обозначают зональные (т — 0), тессеральные (0 < т < п) и секаториальные (т — п) коэффициенты модели, зависящие лишь от времени t. Связь этих функций с распределением плотности планеты p(t, r ) имеет следующий вид [19]:
C nm ( t )
1 /‘ (п — т) М J (п + т)
(а у
Рпт(8гпу) cos(тA) p(t, r ) dr,
S пm ( t ) — М
(п — т)!
(п + т)!
(а у
Рпт(згпу) sin(тA) p(t, r ) d r ,
М — / p(t, r ) d r , C пm (t) — C пm (t)/N пm
S пm ( t) — S пm ( t ) /N пm •
Интегрирование здесь производится по всему объему Земли. Зависимость Cпm(t) и Sпm (t) от времени объясняется океаническими и атмосферными приливами [20], а также перераспределением масс в недрах планеты [21]. В настоящей работе авторы не рассматривают зависимость Cпm(t) и Snm(t) от времени. В этой связи переменная t будет опускаться в дальнейшем изложении. Корректность такого допущения будет рассмотрена в заключении работы.
Существует четыре основных подхода для вычисления усеченного ряда (1) и его градиента VU [22]. Первый п:з них заключается в прямом суммировании выражения (1) с помощью рекуррентных соотношений для присоединенных полиномов Лежандра. Алгоритм расчета U и VU подробно описан в [19]. Поскольку суммирование выполняется от больших слагаемых к меньшим (от п — 0 до п — N), такой подход имеет невысокую точность. Подход Шернинга - Кленшоу [23], [24], [25] лишен этого недостатка. Он представляет собой обратное трехчленное суммирование Кленшоу, примененное к присоединенным полиномам Лежандра. Как первый, так и второй подходы имеют особенности, препятствующие корректному определению производных U на полюсах геоцентрической системы. Для преодоления этой проблемы были разработаны методы Пайнса [26] и Каннингема -Метриса [27], [28]. Отличительной особенностью этих подходов является использование декартовых координат для проведения суммирования.
Арифметическая сложность всех четырех подходов растет квадратично с ростом степени N. На рис. 1 представлена, зависимость времени расчета, градиента. VU от степени N для рекурсивного алгоритма. Шернинга. - Кленшоу.
Согласно [18], для получения прецизионной точности на низких орбитах степень модели N должна быть не меньше 70. При таких параметрах расчет гравитационного поля Земли является наиболее ресурсоемкой стадией определения траекторий космических тел.
Для снижения вычислительных затрат при прогнозировании орбит авторы предлагают 'заменить функцию U на заранее рассчитанный алгебраический нитерполяит U. В разде- ле 2 рассмотрена возможность использования трикубического сплайна [29] для приближения потенциала тяготения U и его градиента VU. В разделе 3 проведено исследование применения многомерной интерполяции на узлах Чебышева - Лиссажу [30]. В обоих разделах проведены оценки ошибок интерполяции и необходимого объема информации для хранения интерполянтов. Проанализированы ошибки прогнозирования орбит, связанные с подменой функции U на ее интерполянт. В заключении статьи обсуждены возможности использования подхода для изменяющегося во времени гравитационного потенциала Земли, сделаны выводы о применимости предлагаемого подхода и намечены задачи для дальнейшего исследования.
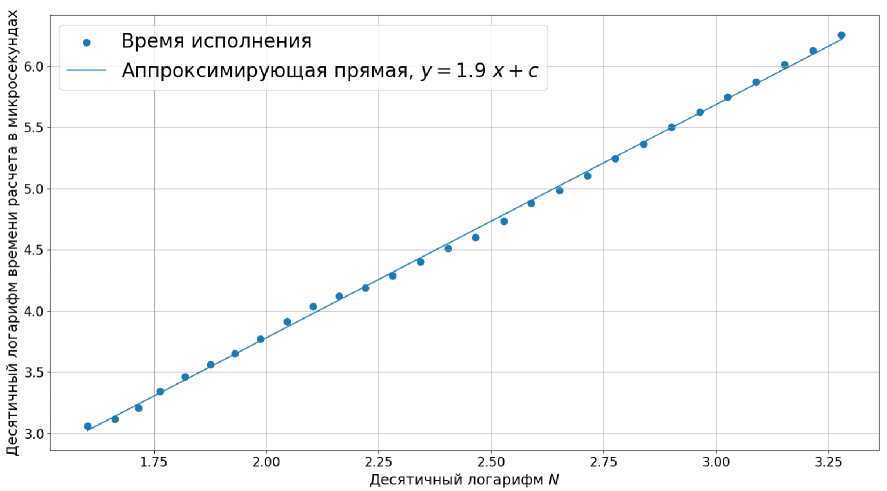
Рис. 1. Зависимость времени расчета градиента VU от степени модели N в логарифмическом масштабе. Расчеты проведены при помощи процессора. Ryzen 5 4500
-
2. Трикубическая интерполяция гравитационного поля
-
2.1. Построение интерполянта
В этом разделе рассмотрено приближение функции U трикубическим сплайном [29].
Построению интерполянта предшествует разбиение околоземного пространства на одинаковые кубы (ячейки) с ребром Һ. Далее в каждом кубе потенциал U и его градиент VU приближаются алгебраическими функциями U и VU:
U= Е ^ X^ ^, i,j,k =0
H i-1 3 k
U x — / v ^ i,j,k ^ X У ^ ,
-
i = 1 ,j,k =0
U — Е a i,j,k k ХгУ3 z^.
-
~ / — — ~ \ T
VU — (U^U j, ,Uz)
H i 3-1 k
Uy — / v ai,j,k 3 X у z , j=1,i,k=0
Здесь (x, у, z) — декартовы координаты пространства, ai,j,k — коэффициенты сплайна, подлежащие определению. Расчет коэффициентов представляет собой решение системы линейных алгебраических уравнений с матрицей, зависящей только от ребра куба Һ. Правая часть линейной системы может быть вычислена с использованием следующих величин в вершинах куба:
-
1) функции U:
-
2) частных производных UX,U y ,UZ",
-
3) вторых смешанных производных UX y , UXZ , U y Z\
-
4) третьей смешанной производной UX y Z.
Рекурсивный алгоритм для расчета величин 1) - 3) изложен в [26]. Для вычисления 4) авторами были получены рекурсивные формулы. Используя обозначения из [26], выражение для UX y Z можно записать следующим образом:
U xyz = Ь 1 + Ь 2 + Ь 3 + Ь 4 + Ь 5 ,
Nп
Ь1 = 52 ^ЛТ 52 т(т - 1)(т - п - І^РпДи) Hn,m(s,t), п=0
Nп
Ь2 = «t(1 -Л) £ £ ;.
п=0
Nп
Ьз = -stti ^ ^-3 52 (П + т + 5) Pn+2,m+2(u)Dn,m(s, t), п=0
Nп
Ь4 = ^52 ^2-3 52 т(^ -т + 1) Tn+2,m+iCu)Pn,m(s,t), п=0
Nп
Ь5 = t^ ^^ У2 т(п -т + 1) Рп+2,т+1Си)£п,т(М). п=0
Построенный интернолянт U приближает функцию U с четвертым порядком точности, а градиент VU с третьим порядком точности.
-
2.2. Исследование интерполяции
Исследование интерполяции проводилось на модели EGM2008 при N = 64. Интерполянт был построен в сферическом слое вокруг Земли, ограниченном сферами с радиусами 6400 км и 7400 км. Корректность реализации подтверждалась путем сравнения градиента исходной функции VU и градиента интерполянта VU при нескольких разбиениях околоземного пространства. Размер ребра куба разбиений Һ варьировался от 35 км до 140 км. На рис. 2 представлена зависимость десятичного логарифма относительной ошибки интерполяции градиента от десятичного логарифма ребра Һ. Относительная ошибка интерполяции градиента оценивалась как максимальное значение ||VU -VU ||/||VU|| в случайном наборе из 104 точек внутри области интерполяции. Угловой наклон аппроксимирующей прямой близок к теоретическому порядку точности интерполянта, что свидетельствует о корректности реализации.
В табл. 1 представлена зависимость ошибки интерполяции от длины ребра Һ и информационный объем, необходимый для хранения интерполянта.
При высокоточном предсказании траекторий необходимо учитывать возмущающие факторы, имеющие величину 10-8 - 10-9 м/с2. Следовательно, применение трикубической интерполяции для прецизионного прогнозирования орбит требует колоссальных объемов информации для хранения интерполянта. Это делает ее неприменимой для рассматриваемого класса задач.
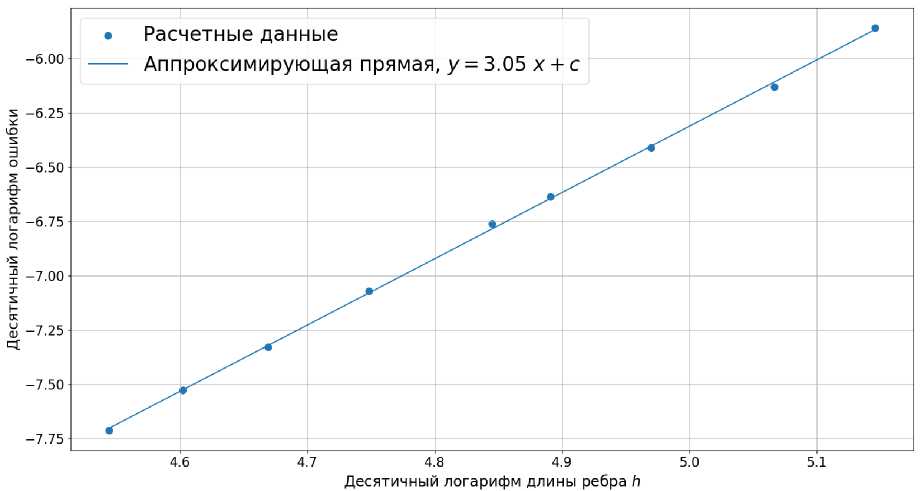
Рис. 2. Зависимость логарифма, относительной ошибки интерполяции от десятичного логарифма, длины ребра. Һ в метрах
Таблица!
|
Количество кубов, 106 |
Относительная ошибка, интерполяции, 10-10 |
Информационный объем, Гб |
|
17.1 |
40.72 |
16.31 |
|
135.8 |
5.14 |
130.46 |
|
461.8 |
1.53 |
440.31 |
|
1094.4 |
0.64 |
1043.70 |
|
2137.5 |
0.33 |
2038.47 |
-
3. Интерполяция гравитационного поля с использованием узлов Чебышева — Лиссажу
В этом разделе рассмотрено приближение функции U интерполянтом на узлах Чебышева. - Лиссажу [30].
ЗЛ. Построение интерполянта
Для построения интерполянта. сферический слой околоземного пространства, разбивался на ячейки. В геоцентрических координатах (р, р, А) ячейки представляли собой одинаковые прямоугольные параллелепипеды. В каждой ячейке сетки функция U и ее градиент VU приближались алгебраическими функциями U 1i VU:
L
U= £ Ci , j , kTi(r)Tj(р)Тк (А), i,3,k =0
L
U = £ Ci,3,k T’(r)T3(^)Тк(А), i=1,3,k=0
L
U a = £ C i, 3 ,k T i (r)T3(р)Т к (А).
VUT = ЦХ A,Ua) J (r,p,A),
L
Uv = £ C i,3,k T i (r)T ' (p)T k (А),
3 =i ,i,k =o
За 7}(ж) обозначен многочлен Чебышева степени г, за J(т,ір,Х) — матрица Якоби геоцентрических координат (р, ^, А) по декартовым координатам (ж,^,г), за L — количество узлов по каждой координате. Числа C i,j,k представляют собой коэффициенты интерполяции. Линейные уравнения на коэффициенты следуют из равенства функции U и ее интерполянта U в узлах Чебышева - Лиссажу. Узлы являются отображением точек Чебышева - Гаусса - Лобатто на кривые Лиссажу. Положение этих узлов в кубе К = [-1,1] х [-1,1] х [-1,1] для интерполянта с L = 5 представлено на рис. 3.
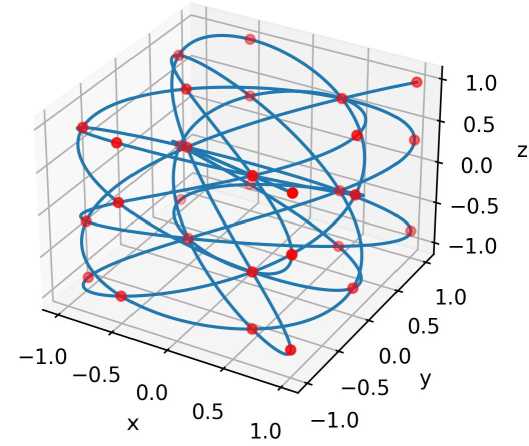
Рис. 3. Узлы Чебышева - Лиссажу в кубе К
Построенный интерполянт имеет порядок точности L + 1, а градиент VU приближается с порядком L.
-
3.2. Исследование интерполяции
Как и в предыдущем разделе, для исследования использовалась модель EGM2008 с N = 64. Интерполянт был построен в сферическом слое вокруг Земли, ограниченном сферами с радиусами 6400 км и 7400 км. Корректность интерполяции проверялась при L = {5,10,15}. На рис. 4 представлены зависимости логарифма относительных ошибок интерполяции градиента от количества ячеек по одной координате. Относительная ошибка градиента ||VU -VU || / |VU|| оценивалась так же, как и в предыдущем разделе. Количество ячеек по каждой из переменных т, у и А принималось одинаковым. На рис. 4 изображены аппроксимирующие прямые. Коэффициенты наклона прямых свидетельствуют о корректности интерполяции.
В табл. 2 представлены количество ячеек, относительная ошибка интерполяции и информационный объем, необходимый для хранения интерполянта. Приведенные значения свидетельствуют о возможности применения рассматриваемой интерполяции для прецизионного прогнозирования орбит. Действительно, достижение высоких точностей (10-9 м/с2) может быть получено при небольшом информационном весе интерполянта.
Для наиболее точного интерполянта с L = 15 был выполнен анализ ошибки прогнозирования орбиты, связанной с подменой VU нa VU. Рассматривались круговые орбиты с полуосями в интервале от 6800 км до 7350 км, наклонениями и долготами восходящих узлов в интервалах от 0 до к и от 0 до 2т соответственно. Всего было рассмотрено 104 орбит. Для каждой из орбит был выполнен ее прогноз на день и на один месяц. При прогнозировании учитывалось лишь гравитационное тяготение Земли. Прогноз выполнялся методом Эверхарта 15 порядка точности [10], [31]. Шаг интегрирования выбирался таким образом, чтобы снизить ошибку численного метода до предельного порога, определяемого представлением чисел в памяти компвютера. Для каждой орбиты было проведено два расчета — с обычным суммированием гравитационной силы и предлагаемой авторами интерполяцией. Ошибка, вызванная новым подходом, оценивалась как максимальная разница между двумя траекториями среди всех орбит. Она представлена в табл. 3.
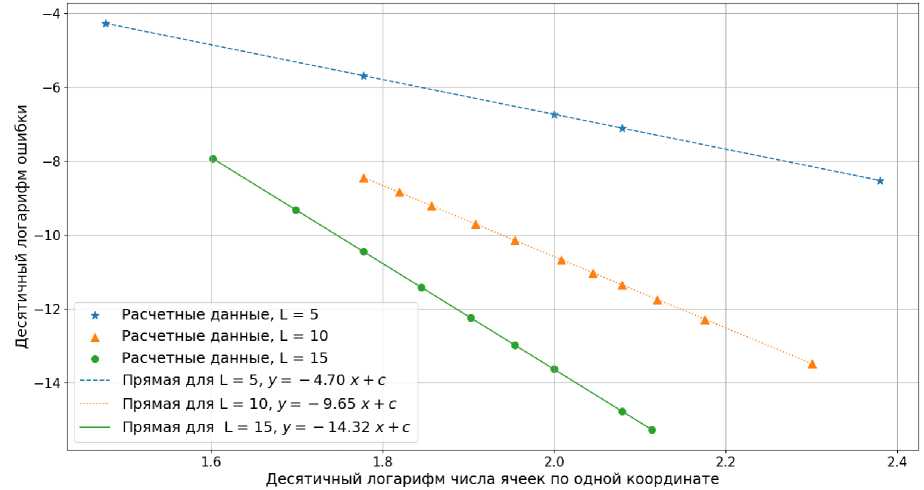
Рис. 4. Зависимость десятичного логарифма, относительной ошибки интерполяции от десятичного логарифма количества ячеек по одной координате для L = 5, 10 и 15
Т а б л и ц а 2
|
L |
Количество ячеек, 106 |
Относительная ошибка интерполяции |
Информационный объем, Гб |
|
1.0 |
1.78 10-7 |
0.09 |
|
|
5 |
1.7 |
7.57 10-8 |
0.17 |
|
13.8 |
2.91 10-9 |
1.17 |
|
|
1.0 |
2.09 10-11 |
0.62 |
|
|
10 |
3.3 |
5.08 10-13 |
3.02 |
|
4.1 |
3.26 10-14 |
4.02 |
|
|
1.0 |
2.29 10-14 |
1.51 |
|
|
15 |
1.5 |
3.11 10-15 |
8.25 |
|
2.0 |
1.34 10-15 |
3.32 |
Т а б л и ц а 3
|
Количество ячеек, 106 |
1.0 |
1.5 |
2.0 |
|
Дневная ошибка, 10-4 м |
6.7 |
3.4 |
1.1 |
|
Месячная ошибка, 10-1 м |
6.0 |
2.9 |
1.2 |
Определение градиента, гравитационного потенциала, с использованием заранее построенного интерполянта требует некоторого времени. Интерполяционный подход является целесообразным лишь тогда, когда время прямого расчета градиента VI/ существенно выше времени расчета интерполированного значения VU. В табл. 4 представлено отношение временных затрат на вычисление VU и VU. Вычисление VU осуществлялось с помощью алгоритма Шернинга - Кленшоу. По вертикали отложена степень модели N, а по горизонтали количество узлов L по одной координате в единичном кубе.
Т а б л и ц а 4
|
L |
||||||
|
10 |
И |
12 |
13 |
14 |
15 |
|
|
8 |
0.6 |
0.4 |
0.3 |
0.3 |
0.3 |
0.2 |
|
16 |
2.3 |
1.8 |
1.4 |
1.2 |
1.0 |
0.9 |
|
N 32 |
9.4 |
7.0 |
5.4 |
4.7 |
4.0 |
3.8 |
|
64 |
37.5 |
28.2 |
21.7 |
19.0 |
16.1 |
15.0 |
|
128 |
150.0 |
112.7 |
86.8 |
75.9 |
64.3 |
60.0 |
Приведенные значения показывают, что предлагаемый подход наиболее эффективен при N > 32. При низких N, например при N = 16, использование интерполяции нецелесообразно.
-
4. Заключение
В работе предложен способ ускорения вычисления гравитационного тяготения Земли при помощи алгебраических интерполянтов. Рассмотрено два типа интерполяции — трику-бический сплайн и алгебраическая интерполяция на узлах Чебышева - Лиссажу. Показано, что использование трикубического сплайна нецелесообразно ввиду больших затрат на хранение коэффициентов интерполянта. Интерполяция на узлах Чебышева - Лиссажу, напротив, не требует большого информационного объема для хранения коэффициентов, а также обеспечивает высокую точность. Ее применение способно обеспечить вычислительно эффективное приближение силы гравитационного тяготения.
Как было замечено во введении, гравитационный потенциал Земли зависит от времени. Следовательно, прямое использование разработанного авторами подхода является не до конца корректным. Это обстоятельство можно разрешить следующим образом. Согласно [18], для практических приложений зависимость коэффициентов Cnm(t) и Snm (t) от времени следует учитывать лишь при п < 10. Поэтому гравитационный потенциал можно разделить на две составляющие: зависящую от времени часть с малым количеством слагаемых и оставшуюся часть, суммирование которой несет большие вычислительные затраты. Авторы предлагают применять интерполяцию лишь ко второй части, а для первой использовать существующие алгоритмы суммирования.
В настоящей работе не рассмотрена задача выбора оптимального количества ячеек интерполяции для обеспечения заданной точности. Поскольку функция (1) имеет различный характер по каждой из трех геоцентрических координат, то целесообразно использовать разное количество ячеек по переменным г, ^и А. Помимо этого, разумно увеличивать размер ячеек с ростом расстояния от центра Земли г. Это объясняется стремлением к нулю производных высоких порядков функции U, определяющих ошибку интерполяции. Эти вопросы будут рассмотрены авторами в следующих работах.
Список литературы Об интерполяции гравитационного поля Земли
- Эбауэр К.В. Исследование возмущенного движения исз «Блиц» // Известия высших учебных заведений. Геодезия и аэрофотосъемка. 2013. № 5. С. 22–28.
- Васильев В.П. [и др.]. Прецизионный КА «Блиц-М» // Метрология времени и пространства. 2014. С. 197–197.
- Соколов А.Л., Акентьев А.С., Ненадович В.Д. Космические ретрорефлекторные системы // Светотехника. 2017. Т. 4. С. 19–23.
- Акентьев А.С. [и др.]. Ретрорефлекторный сферический спутник // Оптика и спектроскопия. 2015. Т. 119, № 4. С. 588–593.
- Paolozzi A., Ciufolini I., Vendittozzi C. Engineering and scientific aspects of LARES satellite // Acta Astronautica. 2011. V. 69, N 3–4. P. 127–134.
- Tapley B.D., Reigber C. The GRACE mission: status and future plans // EGS General Assembly Conference Abstracts. 2002. P. 4819.
- Kornfeld R. P., et al., GRACE-FO: the gravity recovery and climate experiment follow-on mission // Journal of spacecraft and rockets. 2019. V. 56, N 3. P. 931–951.
- Lukosz M.A., Hejmanowski R., Witkowski W.T. Evaluation of ICEYE Microsatellites Sensor for Surface Motion Detection – Jakobshavn Glacier Case Study // Energies. 2021. V. 14, N 12. P. 3424.
- Castelletti D., et al., Capella space first operational SAR satellite // 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS. IEEE. 2021. P. 1483–1486.
- Авдюшев В.А. [и др.]. Численное моделирование орбит небесных тел. Томск: Издательский дом Том. гос. ун-та, 2015.
- Бордовицына Т.В., Авдюшев В.А. Теория движения искусственных спутников Земли. Томск: Издательский дом Том. гос. ун-та, 2007.
- Zavialova N.A., et al., Methods for accurate ballistics calculations for multi-satellite constellations // Advances in the Astronautical Sciences. 2020. P. 91–98.
- Lemoine F.G., et al., The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM96. 1998. № NAS 1.60: 206861.
- Pavlis N.K., et al., The development and evaluation of the Earth Gravitational Model 2008 (EGM2008) // Journal of geophysical research: solid earth. 2012. V. 117. N B4.
- Tapley B., et al., The GGM03 mean earth gravity model from GRACE // AGU Fall Meeting Abstracts. 2007. V. 2007. P. G42A-03.
- Ince E.S., et al., ICGEM–15 years of successful collection and distribution of global gravitational models, associated services, and future plans // Earth system science data. 2019. V. 11, N 2. P. 647–674.
- Бордовицына Т.В. Современные численные методы в задачах небесной механики. Москва: Наука, 1984.
- Petit G., Luzum B. IERS Conventions (2010) // IERS Conventions Centre. 2010.
- Vallado D.A. Fundamentals of astrodynamics and applications. V. 12. Springer Science and Business Media, 2001.
- Lyard F., et al., Modelling the global ocean tides: modern insights from FES2004 // Ocean dynamics. 2006. V. 56. P. 394–415.
- Wahr J. Correction and update to The earth’s C21 and C21 gravity coefficients and the rotation of the core // Geophysical Journal International. 1990. V. 101, N 3. P. 709.
- Casotto S., Fantino E. Evaluation of methods for spherical harmonic synthesis of the gravitational potential and its gradients // Advances in Space Research. 2007. V. 40, N 1. P. 69–75.
- Clenshaw C.W. A note on the summation of Chebyshev series // Mathematics of Computation. 1955. V. 9, N 51. P. 118–120.
- Tscherning C.C. Computation of the second-order derivatives of the normal potential based on the representation by a Legendre series // Manuscripta geodaetica. 1976. V. 1, N 1. P. 71–92.
- Tscherning C.C., Poder K. Some geodetic applications of Clenshaw summation // 8th Symposium on Mathematical Geodesy. 5th Hotine Symposium. 1981.
- PinClenshaw C.W. es S. Uniform representation of the gravitational potential and it’s derivatives // AIAa Journal. 1973. V. 11, N 11. P. 1508–1511.
- Cunningham L.E. On the computation of the spherical harmonic terms needed during the numerical integration of the orbital motion of an artificial satellite // Celestial mechanics. 1970. V. 2, N 2. P. 207–216.
- Metris G., Xu J., Wytrzyszczak I. Derivatives of the gravity potential with respect to rectangular coordinates // Celestial Mechanics and Dynamical Astronomy. 1998. V. 71. P. 137–151.
- Lekien F., Marsden J. Tricubic interpolation in three dimensions // International Journal for Numerical Methods in Engineering. 2005. V. 63, N 3. P. 455–471.
- Dencker P., Erb W. Multivariate polynomial interpolation on Lissajous–Chebyshev nodes // Journal of Approximation Theory. 2017. V. 219. P. 15–45.
- Everhart E. Implicit single-sequence methods for integrating orbits // Celestial mechanics. 1974. V. 10, N 1. P. 35–55.


