Об использовании тензора логарифмической деформации

Тензор логарифмической деформации в настоящее время является одной из наиболее попу лярных мер деформации тела при решении геометрически нелинейных задач. Он представляет собой обобщение скалярной логарифмической деформации

введенной Людвигом в 1909 г., перенесенной на область тензоров [1]. Идея Людвига состояла в том, чтобы сравнивать текущую длину растягиваемого стержня не с начальной длиной 10, как при использовании обычной инженерной деформации

1 — 1A

Е =   - = l0

а с длиной стержня в предыдущем состоянии. Логарифмическая деформация (1) однозначно выражается через инженерную деформацию e = ln (1 + е)(3)

и наоборот, инженерная выражается через логарифмическую

Е = exp( e) — 1.(4)

Таким образом, зная одну, легко получить другую. Для величины e Людвиг в свое время ввел термин effective specific strain - особая эффективная деформация , а несколько позже Надаи предложил новое название - натуральная деформация [2]. В настоящее время широкое распространение получили термины: истинная деформация и логарифмическая деформация .

В 1928 г. Генки [3] предложил распространить идею Людвига на случай трехмерной деформации, введя по аналогии с выражением (3) тензор логарифмической деформации, иногда называемый его именем - тензором Генки e = ln(I + е).                                               (5)

Здесь и ниже тензоры и векторы обозначены жирными символами - для того, чтобы отличать их от скаляров. В выражении (5) е - это тензор инженерной деформации, связывающий векторы 10 волокон тела в начальном состоянии (до деформирования) с векторами l в деформированном состоянии

A l = е - l ₀,       A l = l — l ₀,

I - единичный тензор. Сумму тензора е и единичного тензора обычно называют тензором удлинений (иначе, тензор растяжения или тензор коэффициентов длины )

U = I + е .                                       (7)

В 1956 г. Дойл и Эриксон [4] ввели понятие обобщенной деформации

E ⁽ m ⁾ = ^— ( и m - 1 ) .                                     (8)

m

Здесь разные значения m соответствовали разным мерам деформации. В частности, при m = 0 у Дойла и Эриксона получился тензор логарифмической деформации.

Таким образом, как и в случае одноосной деформации, в общем случае имеются две альтернативные меры деформации: инженерная и логарифмическая. И, как показывает практика, логарифмическая деформация более популярна среди инженеров-механиков (при решении геометрически нелинейных задач). Это, по-видимому, объясняется тем, что использование логарифма позволяет заменять произведения суммами, упрощая решение задач. Например, чтобы найти относительное изменение объема элемента твердого тела, можно вместо традиционного выражения

А V

V o

= ^{(1 +} ^ 1 ^{)(1 +} ^ 2 ^{)(1 +} ^ э ) ^- 1,

использовать более простое:

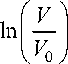
= e 1 ⁺ e 2 ⁺ e 3

Условие несжимаемости среды при этом принимает вид е1 + е2 + е3 = 0, то есть тензор логарифмической деформации напоминает девиатор. Удобно также разделять логарифмическую деформацию e на упругую составляющую и неупругую:

e = e _е ⁺ e p .                                             ⁽¹²⁾

Эта сумма напоминает геометрически линейный подход.

При решении инженерных задач тензор логарифмической деформации связывают с некоторыми мерами напряжений, например, Кирхгофа [5] или Коши [6, 7]. Однако достоверность полученных результатов при этом вызывает серьезные сомнения [8]. Ниже будет показано, что использование тензора логарифмической деформации имеет смысл только в главных осях.

Вычисление тензора логарифмической деформации

Известно [9], что для получения какой-либо функции двухвалентного тензора T достаточно знать его главные числа { X i } и главные направления, которые обычно задают единичными векторами { c i } - главными векторами. Особенность главных векторов состоит в том, что при скалярном умножении на тензор T они не поворачиваются:

T • C i =X c .                                     (13)

Соответствующее характеристическое уравнение

| T — V\ = 0                                    (14)

позволяет найти главные числа и векторы тензора T . Для вычисления функции тензора необходимо записать его в главных координатах, применив эту функцию к главным значениям. У симметричного тензора все главные числа вещественны, а главные направления взаимно ортогональны. Следовательно, натуральный логарифм тензора U определяется в трехмерном пространстве суммой трех слагаемых

In U = ^ln( u i ) ci ci ,                                            ⁽¹⁵⁾

где i =1^3, ui - это главные числа тензора U, а ci - векторы декартового базиса, совпадающие с главными направлениями тензора U. Отметим, что, согласно выражениям (7) и (13), тензоры U и е имеют одинаковые главные направления, а их главные числа отличаются на единицу ui = Ei+ 1.                                           (16)

В матричной форме выражение (16) имеет вид

Механика

[ e ] =

ln u ₁

ln u ₂    0

0    ln u ₃

При записи матричных выражений следует помнить о том, в каком именно базисе это сделано. Например, выражение (17) содержит координаты тензора, записанного в декартовом базисе, направления которого совпадают с главными направлениями этого тензора. В другом базисе координаты будут другими.

Деформации и жесткие повороты

При неоднородном деформированном состоянии тела обычно рассматривают деформирование элементарных объемов, материальные волокна которых бесконечно малы. Тогда деформированное состояние каждого из таких объемов можно принять однородным. В этом случае волокна, прямые до деформирования, при деформировании не искривляются, и их удобно обозначать векторами. При деформировании элементарного объема его главные волокна (волокна, описываемые главными векторами тензора деформации) не поворачиваются, а только удлиняются или укорачиваются. Однако деформирование соседних элементарных объемов способно вызывать жесткий поворот последнего, при этом его главные волокна поворачиваются. Оператором линейной связи между векторами элементарных волокон в начальном и деформированном состоянии в этом случае служит тензор дисторсии F l = F ■ lо, (18) включающий в себя деформацию элементарного объема и его жесткий поворот

F = R ■ U = V ■ R . (19) В этом выражении, которое обычно называют полярным разложением тензора дисторсии, U и V -это соответственно правый и левый тензоры удлинений (симметричные тензоры):

U = Еи +1, V = Еу +1, (20) выраженные соответственно через правый ги и левый eV тензор инженерной деформации, а R -тензор жесткого поворота на угол ф против часовой стрелки вокруг оси, заданной единичным вектором n

R = nn + ( I — nn ) cos ф + Э ■ и sin ф .

Здесь Э = —5 _ijk e i e _у e _k - это тензор Леви-Чевитты ( 5 _{i jk} - символ Веблена). На плоскости, перпендикулярной вектору и , в декартовом базисе матрица этого тензора имеет довольно простой вид

[ ^R ] =

COS ф sin ф

— sin ф cos ф

.

Поскольку тензор жесткого поворота является ортогональным тензором (то есть R ^{— 1} = R T ), связь между левым и правым тензором удлинений, следующая из полярного разложения дисторсии (19), линейна

V = R ■ U ■ R T . (23)

Это выражение означает, что левый тензор удлинений получается поворотом правого тензора на угол жесткого поворота.

Полярная декомпозиция тензора дисторсии основана на следующих соображениях. На рис. 1 показана схема дисторсии элементарного объема тела (для наглядности рассмотрена двумерная задача), в результате которой материальные волокна вытянулись (либо укоротились) и повернулись. Произвольный вектор l0, отвечающий некоторому множеству материальных волокон в на чальном состоянии, изменил свою длину и направление. Сейчас это вектор lF = F ■ l0, отвечающий тому же множеству материальных волокон в деформированном состоянии. Этот вектор можно представить двумя способами. В первом способе сначала рассматривают деформацию элементарного объема, получая при этом вектор lU = U ■ l0, а затем его жесткий поворот

If = R ■ lu = UU ■ lо.

F

В результате тензор дисторсии выражается через правый тензор растяжений F = R • U. Во втором способе сначала рассматривают жесткий поворот, получая вектор lR = R • 10, а затем дефор мацию

If = V • Ir = RR • lо.

F

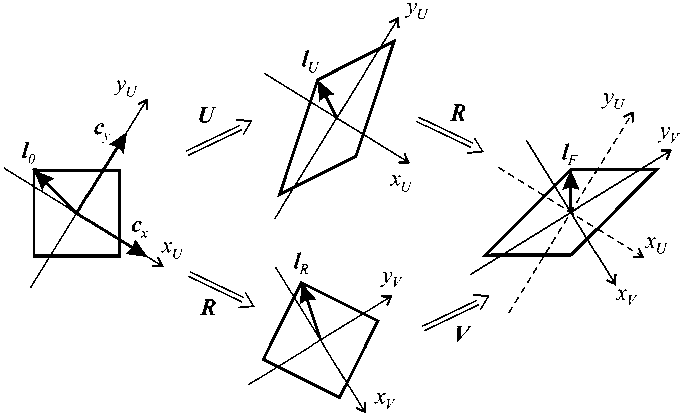
Рис. 1. Дисторсия элементарного объема

Тензор дисторсии при этом выражается через правый тензор растяжений F = V • R .

По аналогии с введением двух тензоров удлинений - правого и левого, вводят два тензора логарифмической деформации. Взятие логарифмической функции тензоров U и V , дает соответственно правый и левый тензоры логарифмической деформации:

eU = ln U , e_V = ln V . (26)

Смысл координат

Обычно тензоры логарифмической деформации записывают в главных координатах, так как именно эта форма записи позволяет извлечь из них полезную информацию в виде логарифмических деформаций главных волокон. Например, координаты тензора eU = lnuxcxcx + lnuycycy , (27) записанного в декартовом базисе { cx, cy} (см. рис. 1), векторы которого направлены вдоль главных осей хи и yU этого тензора, представляют логарифмические деформации главных волокон. Этим, собственно, и ограничивается полезная с точки зрения механики информация, содержащаяся в этом тензоре. Получить какую-либо информацию о деформировании других волокон с помощью этого тензора невозможно.

Что касается тензора eV, то он согласно выражениям (23) и (26) получается жестким поворотом правого тензора удлинений eV = ln( R • U • R T).

Следовательно, его главные координаты ( x_V и y_V на рис. 1) совпадают с главными координатами тензора eU ( x_U и y_U на рис. 1). По сути, тензор e_V содержит ту же информацию, что и тензор eU . Однако для получения этой информации необходимо не только направить базисные векторы вдоль главных осей, но и следить за их жестким поворотом, что усложняет координатную и матричную форму записи тензорных выражений [10].

В отличие от тензора логарифмической деформации (левого или правого), тензор инженерной деформации содержат существенно больше полезной информации о деформировании тела. Во-первых, согласно выражению (6), его проекция на вектор, задающий некоторое материальное волокно, дает вектор изменения этого волокна, определяющий его удлинение (укорочение) и поворот. Во-вторых, столбцы матрицы тензора е представляют изменения базисных векторов, причем базисные векторы могут и не совпадать с главными направлениями тензора е . В-третьих, диагональные элементы матрицы [ в ] представляют линейные деформации волокон в направле-