Об истории и ограничениях диагонального метода

1.    Предисловие

При рассмотрении подпериодов 5-го периода развития науки, и сопоставлении подпериодам 5-го периода определенных уровней понимания причинности, (см. [17], [21], [20]) подпериоду 5.3 развития научной методологии соответствуют теории, рассуждающие о последовательностях причинноследственных связей (древовидных рассуждениях): будь это в селекции "скрещивание разных сортов, простое и сложное многосту-пенное" [20], в химии "периодический закон" [21], "аксиоматизация" в основаниях математики [19] или метод последовательных приближений в решении прикладных задач [17, с. 97–99]. На тех же гносеологических основаниях выделения подпериодов развития методологии науки [17, с. 96], рассуждения о связях бесконечных последовательностей между собой соответствуют подпериоду 5.3.

Диагональный метод – это некоторый способ рассуждения о связи между некоторыми бесконечными последовательностями.

2.    Методологические основания

Для иллюстрации особенностей рассматриваемых диагональных рассуждения служат современные результаты в этой области.

В работах [16], [19] была доказана счетнoсть древовидной структуры десятичных обозначений чисел на прямой:

"Теорема 1 (О счетности десятичных обозначений чисел) Число десятичных обозначений чисел – счетно" [16, с. 54], [19, с. 49].

В работе [22] была доказана теорема о том, что невозможно построить всюду плотный линейный список десятичных обозначений чисел:

"Теорема 2 (Об отделимости). Для десятичных обозначений чисел на прямой выполняется условие отделимости (между любыми двумя обозначениями найдется счетнобесконечное количество промежуточных)" [22, с. 20].

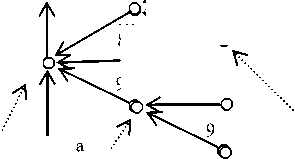
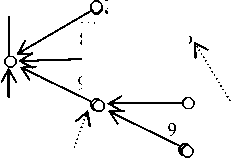
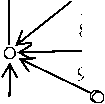
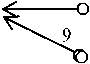
Таким образом, древовидная структура десятичных обозначений чисел на прямой (см. рис. 1) является счетным списком, для которого между любыми двумя десятичными обозначениями можно вписать еще счетное цепь

10-деревьев

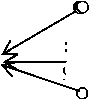
98 о

1       m+1

узел цепи

b

-о

0       m)

–1      m–1

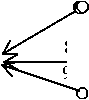
98 о

f(b)

f(a)

-о

о

-о

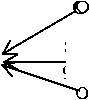
98 о

слой 1        2        3

Рис. 1. Цепь 10-деревьев [ 19 , с. 51]

же число обозначений (ветвей этого дерева); подробное доказательство см. в [22, с. 20]. Отсюда следует, что все линейные списки (не учитывающие древовидность структуры), пусть и бесконечной выборки из десятичных обозначений, не будут всюду плотными, их всегда можно дополнить новыми, не вошедшими в этот список ветвями, при этом и это их пополнение остается счетным.

3.    История диагонального метода

В 1890 г. Г. Кантор в работе "Об одном элементарном вопросе учения о многообразиях" применил диагональные рассуждения1.

Им рассмотрены бесконечные последовательности Ek вида

Ek=(a1,k, a2,k, a3,k, a4,k, …).        (1)

Он пишет: "Пусть М – совокупность всех элементов Е. <…> Теперь я <Кантор> утверждаю, что такое многообразие М не имеет мощности последовательности 1, 2,..., v.

Это вытекает из следующей теоремы: "Если Е 1 , Е 2 , ..., Е ν , ...– какая-либо просто бесконечная последовательность элементов многообразия М, то всегда существует такой элемент Е₀ многообразия М, который не совпадает ни с каким E ν "" [3, с. 170–171]. И далее им строится диагональный элемент по отношению к некоторому бесконечному списку строк E k вида (1).

В современном изложении эта процедура описана в [7]²: "Предположим, что дано какое-то счетное множество <… десятичных обозначений> чисел α , лежащих на промежутке [0. 1]:

α 1 =0, a 1,1 , a 1,2 , a 1,3 , a 1,4 ,…, a 1,n ,… α ₂=0, a_2,1, a_2,2, a_2,3, a_2,4,…, a_2,n,…  (2)

α _n=0, a_n,1, a_n,2, a_n,3, a_n,4,…, a_n,n,…

Здесь a i,k – k-я десятичная цифра <десятичного обозначения> числа α i . Построим дробь β =0, b 1 , b 2 , b 3 , b 4 ,…, b n ,… диагональной процедурой Кантора, а именно за b 1 примем произвольную цифру, не совпадающую с a 1,1 , за b 2 – произвольную цифру, не совпадающую с a 2,2 и т. д.; вообще, за b n примем произвольную цифру, не совпадающую с a n,n . Эта десятичная дробь < β > не может совпасть ни с одной дробью, содержащейся в перечне (2)" [7, с. 32–33].

Легко видеть, что при построении списка (2), как и совокупности последовательностей вида (1) неявно (не сформулировано в исходных предпосылках Кантором и др.) предполагалось, без учета древовидной структуры десятичных обозначений чисел:

a k+1

ak

a k-1

am

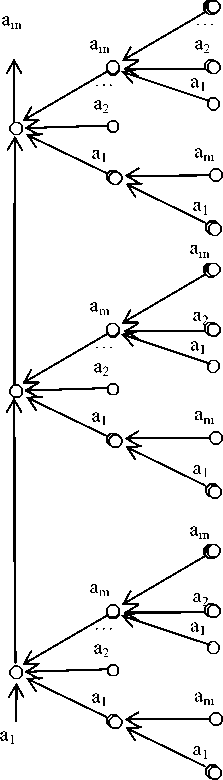
слой 1        2        3

Рис. 2. Дерево слов в алфавите

• а)    что список всюду плотен, т. е. что между любыми Ek1 и Ek2 из (1) невозможно вставить Ek3, и что между любыми αi и αj из (2) невозможно вставить ни одного αk;

• б)    что этот список (1) или (2) исчерпывающ.

4.    Ограничения диагонального метода в логике

Однако, с учетом описанных в пункте 2 результатов, по теоремам 1 и 2 списки вида (1) и (2) не являются всюду плотными и исчерпывающими для десятичных обозначений чисел. Поэтому результат диагональной процедуры говорит лишь о том (в соответствии со свойством отделимости для десятичных обозначений чисел [22]), что если список содержит пусть и счетно-бесконечную последовательность ветвей дерева десятичных обо- значений чисел, то к этой неисчерпывающей3 совокупности ветвей дерева добавляема еще одна его ветвь, отличная от остальных.

Таким образом, рассуждения диагональных процедур не выходят за пределы уже известных результатов непротиворечивой теории множеств с самопринадлежностью, см. теоремы 1, 2 из [22] и [16], [19]. Более значимые ограничения диагональных рассуждений имеют место в нумерациях формальных теорий.

Для метаматематических рассуждений, использующих Гёделеву нумерацию конечного алфавита формальной теории, ограничения действуют именно из-за диагональной структуры представлений выражений теории (и соответственно диагональной структуры соответствующих им Гёделевых номеров). Пусть некоторая формальная теория Т имеет конечный алфавит А: a i , где i= 1,m ; тогда произвольные выражения этой теории имею древовидную структуру (на первом слое – один из символов алфавита, на втором слое – второй, на третьем – третий и т. д.), см. рис. 2. Это дерево обладает свойствами отделимости, между любыми двумя словами (ветвями дерева) вида a k1 a k2 a k3 a k4 … и a r1 a r2 a r3 a r4 … (где k i и r i – индексы символов в алфавите А) находится счетно-бесконечное количество (лексикографически) промежуточных слов, при счетном числе слоев дерева (счетной длине слов), по аналогии с теоремой 2.

Очевидно, что из полного набора слов останется какое-то количество допустимых (корректных записей выражений теории Т), но и для них древовидная структура и отделимость естественно сохраняются. При этом диагональные рассуждения, оперирующие с линейным всюду плотным списком слов теории Т, оперируют с ограниченным его набором (как в случае рассуждений о десятичных обозначениях чисел, см. п. 3), – для такого ограниченного набора выражений теории Т и соответствующих им Гёделевых номеров строится диагональным методом выражение, не всходящее в исходный набор4, – т. е. определяется, что кроме ограниченного набора выражений (ветвей в алфавите А) есть еще некоторое выражение (что соответствует свойству отделимости древовидных структур, теорема 2). То есть всего-навсего устанавливается, что линейный список выражений теории Т не является всюду плотным, – имеет древовидную структуру и обладает свойством отделимости (между двух любых выражений имеется счетное число лексикографически промежуточных).

Заключение

Из ограничений диагонального метода в нумерациях формальных теорий вытекает следующее. Предикативные попытки доказательства теорем Гёделя, использующие диагональные рассуждения, таким образом, могли показаться некорректными; однако короткие непредикативные доказательства этих теорем Гёделя как замена длинным предикативным достаточно давно известны [14], [16].

Вообще непредикативные рассуждения в истории математики давно не являлись чем-то необычным или запретным: "Вся математика – особенно анализ – изобилует непредикативными условиями"5 [9, с. 218]. Использование непредикативных рассуждений позволяет доказать и непротиворечивость теории множеств [14], [15]6.

Что же касается ограничений и истории предикативной процедуры диагонального метода, (появившейся на своем историческом этапе), то они описаны с достаточной ясностью, и указывают на то, что диагональная процедура позволяла лишь доказать попол-нимость упорядоченных фрагментов списков (с древовидной структурой), обладающих свойством отделимости. На своем историческом этапе (до выяснения свойств древовидных структур), описанные диагональные рассуждения вряд ли могли быть другими.