Об истории относительного расстояния в плоской области

Термин «относительное расстояние» появляется впервые в работе Мазуркевича (1916) [7] как нижняя грань диаметров всех связных множеств, соединяющих точки а и b (см. также Куратовского [1, с. 255]).

Определение 1. (Расстояние Мазуркевича) р _м (a,b) = inf diam(E ) , где Е связное множество, соединяющее точки а и b .

Однако основное назначение этого определения — изучение поведения связности многосвязных областей в отдельной точке на границе.

В дальнейшем, в работе Мазуркевича (1936) [8], это определение было применено для изучения простых концов по Каратеодори в плоской области. Однако, как показывают простые примеры, это расстояние не является метрикой простых концов.

Пример 1. Рассмотрим область, представляющую из себя единичный квадрат с выброшенными разрезами

С = { х = 1 - 12 ^ .// е [1/2,1] } .

Тогда две последовательности

К } = (1 - 2^ , 1/2),      { ^   =(1 -     , 3/4)

сходятся к одному и тому же простому концу II рода с телом х = 1, / е [1/2,1] . В то же время

Р м (z' _n ,z” „ ) = 1/4.

М.А. Лаврентьев [2] (1936) ввел понятие относительного расстояния.

Определение 2. (Относительное расстояние Лаврентьева.) Расстояние p _D (z ₁ , z ₂ ) = = min { p ₁ (z ₁ , z ₂ ),p ₂ (z ₁ ,z ₂ ) } между точками области D как минимум: р ₁ — точной нижней грани длин дуг, соединяющих эти точки, и р ₁ точной нижней грани длин дуг, разбивающих D и отделяющих z ₁ , z ₂ от точки 0 E D .

Граничной точкой он называет любую последовательность точек z _n 6 D без предельных точек в D такую, что p _D (z _m ,z _n ) ^ 0 при m,n ^ то . Расстояние между граничными точками t ₁ = { z ^ } ,t ₂ = { z ^ } определяется как

p(t i ,t 2 ,D) = lim p _D (z ^ ,z ;2 ). n ^^

Точки, между которыми нулевое расстояние, считаются идентичными. Введенное определение является метризацией понятия простого конца в смысле Каратеодори. Лаврентьев доказывает, что если область лежит в круге I z | < М и / — конформное отображение на единичный круг с нормировкой, то для любых точек замкнутой области, компактифицированной, как указано выше, справедлива оценка

к

^exp - PD^

< I /(^ 1 ) - / (^ 2 ) | < ^К 1 \[P^Z^) ,

в которой К зависит только от М , а К ₁ — абсолютная постоянная.

В работе [5] Г.Д. Суворовым (1956) был построен контрпример, который показывает нарушение неравенства треугольника для относительного расстояния Лаврентьева. Ниже приводится свой контрпример (рис. 1).

Пример 2. Рассмотрим область, состоящую из двух кругов В ₁ и В ₂ , связанных прямоугольной перемычкой. Радиусы этих кругов равны 1 и 2 соответственно, а длина перемычки равна 1/2, ширина 6 . Точки z ₁ и z ₃ есть центры указанных кругов, а точка z ₂ лежит на радиусе в круге В ₁ в противоположной стороне от В ₂ . Тогда относительное расстояние между z ₁ и z ₂ равно 6 , расстояние между z ₂ и z ₃ равно 1 + 2 + 1/2 . В свою очередь, относительное расстояние между z ₁ и z ₃ min { 2 + 2, 2 + 1 + 1/2 + 1/2 } , таким образом, в данном случае нарушено неравенство треугольника.

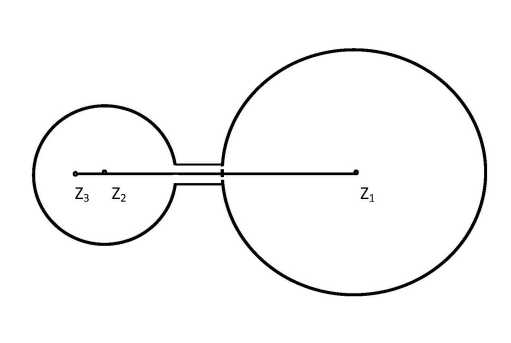
Рис. 1. Контрпример к расстоянию Лаврентьева

В дальнейшем в работах Г.Д. Суворова [6] и его учеников было предложено исправление определения расстояния Лаврентьева таким образом.

Определение 3. (Относительное расстояние Лаврентьева — Суворова)

PD(zi,z2) = min{pi(zi,z2),P2(zi, z2)}, где р1 ( 21 ,22) — инфимум диаметров кривых, соединяющих точки 21,22 внутри области; р2 (21,22) — инфимум диаметров сечений, отделяющих точки 21 и 22 от точки О Е D внутри области D.

Замечание 5. Дело в том, что при доказательстве неравенства треугольника pD (21, 23) < pD (21,22) + pD (22, 23)

не возникает никаких проблем в случае, если минимум для обеих пар точек 2 ₁ , 2 2 и 2 2 , 2 3 достигается либо на р ₁ , либо на р ₂ . Вся задача состоит в том, чтобы доказать, что неравенство выполняется, когда для одной пары точек минимум достигается на р ₁ , скажем на кривой у ₁ , а для другой — на р ₂ , пусть на кривой 7 2 . В этом случае кривые 7 ₁ и у ₂ пересекаются, но в случае, если в определении рассматриваются длины, то объединенная кривая 7 ₁ U 7 2 не может ни разделять, ни соединять точки 2 ₁ и 2 3 .И значит, кривые, соединяющие 2 ₁ и 2 3 , могут иметь длину более чем сумма длин 7 ₁ и 7 2 . В случае использования в определении расстояния диаметров кривых это не так.

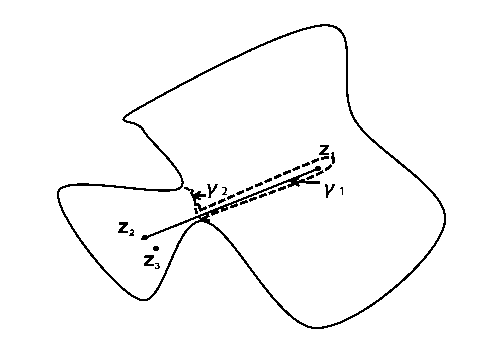
Рис. 2. Неравенство треугольника

Определение 4. (Расстояние Лаврентьева — Миклюкова.) Пусть D — односвязная область и О Е D — фиксированная точка. Если точки a,b Е D , то пусть

р(а, b; О, D) = ш1п{р1 (а, b), р2(a, b)}, где р1 есть точная нижняя грань длин замкнутых кривых 7 С D \ О, отделяющих а и b от точки О и границы dD; р2 есть точная нижняя грань длин дуг, лежащих в D \О и отделяющих а и b от О в области D.

Теорема 1. Расстояние Лаврентьева — Миклюкова удовлетворяет аксиомам расстояния.

Доказательство. Здесь мы с некоторыми изменениями и дополнениями повторим доказательство из [3]. Для доказательства неравенства треугольника

р(2 1 , 2 3 ) <  р(2 1 , 2 2 ) + р(2 2 , 2 3 )

необходимо рассмотреть три случая: 1) минимум для обеих пар точек 2 ₁ ,2 2 и 2 2 ,2 3 достигается на р ₁ ; 2) минимум для обеих пар точек достигается на р ₂ ; 3) минимум для одной пары точек достигается на р ₁ , а для другой пары точек достигается на р ₂ .

В первом случае кривые 71 и 72, близкие к инфимуму, отделяющие точки z1,z2 и точки z2,z3 соответственно, могут как пересекаться, так и содержать одну внутри другой. В случае, если они пересекаются, имеем объединенную кривую, которая отделяет Z1Z3 от dD и О и имеет длину, меньшую, чем сумма 71 и 72. И значит, pi(zi, Z3) < lengh(7i) + lengh^) < pi(zi, Z2) + pi(z2, Z3) + e.

В случае, если они не пересекаются, то они находятся одна внутри другой, и значит, одна из них, скажем 7 1 , отделяет все три точки z 1 ,z ₂ ,z ₃ от О и dD , и мы имеем

P i (z i , Z 3 ) <  lengh(7 i ) <  p i (z i , Z 2 ) + p i (z 2 , Z 3 ) + e.

Во втором случае, если минимум достигается на сечениях, то сечение 7 1 , отделяющее точку О и точки z 1 ,z ₂ , делит область на две связные компоненты: в одной из них лежит точка О , а в другой точки z 1 , z ₂ . В свою очередь, 7 2 делит область на две связные компоненты: в одной из них лежит точка О , а в другой точки z ₂ ,z ₃ . Таким образом, две компоненты содержат общую точку z ₂ , и значит относительная граница этих компонент связности состоит из сечений 7 1 и 7 2 , и значит, она является сечением, длина которого менее чем сумма длин 7 1 и 7 2 .

P 2 (z i , Z 3 ) <  lengh(7 i ) + lengh^) <  p 2 (z i , Z 2 ) + p 2 (z 2 , Z 3 ) + e.

И наконец, третий случай, в котором одна из кривых, приближающих p1, 71 является замкнутой кривой, отделяющей z1,z2 от О и от границы D, а вторая кривая — сечение 72, приближающая p2, отделяет z2,z3 от точки О. В этом случае в той компоненте связности, в которой находятся точки z2,z3, лежит некоторый участок кривой 71, а значит, либо она вся находится в этой компоненте и тогда сечение 72 будет сечением и для точек z1,z3, и тогда имеем p2(zi, Z3) < lengh^) < p2(Z2, Z3) + e.

Либо же кривая 71 пересекает сечение 72. И тогда объединенная кривая 71 72 является сечением (см. рис. 2), и для ее длины имеем p2(zi,Z3) < lengh(7i [J 72) < pi(zi,Z2) + p2(z2,Z3) + e.

Необходимо отметить, что введенное относительное расстояние ничем не отличается от евклидового в случае выпуклой области. В этом случае все длины сечений области имеют большую длину, нежели кривые, соединяющие точки.

В связи с этим можно доказать следующую теорему об искажении относительного расстояния при конформном отображении.

Теорема 2. Пусть /(z) — конформное отображение единичного круга |z| < 1 на область D. Для относительного расстояния имеем следующую оценку pn(/(z1), /(z2)) < С|zi - z2|1/2.

Доказательство. Для двух точек z 1 , z ₂ , лежащих в круге | z | < 1 , обозначим е ^г6 точку пересечения окружности | z | = 1 с прямой z 1 z ₂ , а через р 1 = | е ^г6 — z 1 | р ₂ = | е ^г6 — z ₂ | . Тогда | z 1 — z ₂ | = р 1 — р ₂ . Рассмотрим кривые L _p — образы дуг окружностей С _p = { z = = е¹^ + ре ^г6 ,9 1 < 9 < 9 2 } . Для длин | L _p | по неравенству Коши имеем

| L p | ² = ( j_c |V f | рd9) ² <  . ' ² / |V / ² -'..у ' d9).

Интегрируя от г 1 до г ₂ , получим

/ Г 2                   Г 2            Г 2

| L p | ² dр < ту р ¹ '²dр у рdр у |V / | 2 d9 <  S(D p i p 2 )( | р 1 — р2| ^3/2 ).

Где S(D _r 1 _r 2 ) — площадь фигуры между двумя кривыми L _r 1 L _r 2 . Полагая т 1 = = тах { р 1 , р ₂ } , т ₂ = т 1 + | р 1 — р ₂ | , будем иметь кривые L _p r 1 <  р <  г ₂ , отделяющие точки / (z 1 ), /(z ₂ ) от фиксированной точки О .

Таким образом получаем, что относительное расстояние в образе в области D, будет рп(/(zi),/(z2)) < min |Lp| < С(р1 — р2)1/2 = С|zi — z2|1/2

Г 1 <р<Г 2

Конечно, отсюда легко видеть, что пополнение по метрикам Суворова и Миклюко-ва присоединяет к области простые концы по Каратеодори. Однако это не единственное конформно-инвариантное расширение. В работе (1980) [4] был построен набор метризу-емых конформно-инвариантных расширений плоской области. В связи с этим возникает проблема, неднократно озвученная Г.Д. Суворовым, охарактеризовать расширение по простым концам по Каратеодори среди всех возможных расширений плоской области. Гипотеза о том, что такой характеристикой может быть такая: «расширение по Кара-теодори — единственное, в котором граница гомеоморфна окружности» — неверна (см. [4]). Однако в частных беседах с В.М. Миклюковым им высказывалась идея следующей теоремы.

Теорема 3. Расширение по простым концам по Каратеодори — единственное, в котором расширенная компактифицированная область гомеоморфна замкнутому кругу.

Доказательство. Хорошо известно, что пополнение по простым концам по Каратео-дори превращает область в замкнутый круг. Обратно, если известно, что пополнение гомеоморфно замкнутому кругу | z | <  1 , то фундаментальная система окрестностей точки ^ , лежащей на границе круга | z | < 1 , может быть задана концентрическими кругами | z — ^ | < 1/п . А это значит, что и в нашем гипотетическом расширении плоской области D мы имеем в качестве фундаментальной системы окрестностей цепь вложенных связных односвязных подобластей ш _п . Такие области имеют относительную границу дш _п H D , являющуюся дугами-сечениями области D . То есть ш _п являются цепью сечений, определяющих простой конец.