Об изолированных особенностях квазилинейных уравнений

При a >  0, a' <  0, |V u | ² <  — 2 00 0

0 < (2a'|Vu|2 + a)|(|2 < aij(^ < a|<|2.

При a > 0, a ⁰ >  0

0 < a|(|2 < aij^ < (2a'|Vu|2 + a)|<|2.

Таким образом, матрица коэффициентов [a ij (x, u x i ,u _x j )] оператора Q положительно определена при всех x Е 9 \ 9 0 . Следовательно, оператор Q — эллиптичен в 9 \ 9 о .

Покажем теперь, что оператор Q локально равномерно эллип т ичен на функции и . Рассмотрим любое компактное подмножество 9 множества 9 \ 9 ₀ .

При a > 0, a ⁰ <  0 из ( 2) следует, что оператор Q равномерно эллиптичен на функции и , если |V u | ² <  — 2 0 0 для всех x Е 9 [1, с. 240].

При a > 0, a ⁰ >  0 , согласно (3), оператор Q равномерно эллиптичен на функции и , если 0а - и |V u | ² — ограничены для всех x Е 9 [1, с. 240]. Так как рассматривается значение функции и на компакте 9 , то можно считать, что эти требования выполнены.

Таким о бразом, функция u удовлетворяет сильному принципу максимума в области 9 \ 9 0 [1, с. 42].

Так как в области 9 \ 9 0 выполнен сильный принцип максимума, то r ₀ (m(r ₀ ) = t ₀ ) — точка минимума функции m(r) . Покажем, что m(r) монотонно возрастает. Предположим противное, то есть существуют точки r ₁ и r ₂ такие, что для r ₀ < r 1 < r ₂ выполнено m(r 1 ) >  m(r ₂ ) > m(r ₀ ) . Тогда во внутренней точке области 9 \ 9 0 достигается локальный максимум. Таким образом, имеем противоречие с сильным принципом максимума.

Так как m(r) — монотонная, то существует обратная к ней монотонная функция r(t) , определенная на интервале т ( F ) .

Покажем, что r(t) выпукла вниз на т ( F ) . Предположим обратное, тогда существуют точки a,£, b из промежутка т ( F ) такие, что a < £ < b и

ξ - a

^r(() > |----^{(r(b) — r(}a⁾⁾ + ^r(a) ^ f(£).

b - a

Рассмотрим коническую поверхность C С R n ⁺¹ , полученную вращением графика линейной функции f (t) вокруг оси Ot . Пусть X Е S(£) — точка на поверхности F , расстояние от которой до оси Ot равно r(^) . Точка X расположена вне конуса C , и существует гиперплоскость W , заданная функцией w(x) , отделяющая точку X от C . Так как f (a) = r ( a ) и f (b) = r(b) , то «шапочка» А , срезанная с поверхности F гиперплоскостью W и содержащая точку X , заключена между гиперплоскостями П(а) и П(Ь) . Ее граница д А лежит на гиперплоскости W и компактна. Положим fi ⁰ = { х Е fi \ fi ₀ : (х, и ( х )) Е А } , при этом w ( x ) < u(x) | _{Q 0} и u = w^ •

Функция w(x) является линейной, следовательно, как и функция и(х) удовлетворяет в области fi0 уравнению (1), то есть div(a(|Vu|2)Vu) = div(a(|Vw|2 )Vw).                       (4)

Коэффициенты a ij ( x,p i ,p j ) не зависят от и и согласно (i) являются непрерывно дифференцируемыми функциями переменных p . Таким образом, все условия теоремы единственности решения квазилинейного уравнения выполнены [1, с. 244], следовательно и = w | _{Q 0} . Приходим к противоречию.

Лемма 2. Пусть функция и Е C ⁰ (fi \ fi o ) П C ² (fi \ fi o ) — решение уравнения (1) и пусть выполнены условия (i)-(ii) леммы 1, тогда r ( t ) есть функция класса W 12 _loc на т ( F ) , удовлетворяющая почти всюду на данном интервале дифференциальному неравенству

(о I a r02(t)                         r05(t)

r ^{0 2} (t) + 2— у ----4 I >  (n — 1) ——.               (5)

1                         r(t)

a r ⁰² ( t )

Доказательство. Так как по лемме 1 график функции r(t) является выпуклым вниз на промежутке т ( F ) , то r(t) очевидно принадлежит классу W ^ _loc на т ( F ) [2, с. 70].                                                                                     ^,

Рассмотрим радиально симметричную функцию v(x) = m( | x — x ₀ | ) <  u(x) .

Для любого радиуса r существует точка х * Е S r : m(r) = v(x * ) = u(x * ) . Следовательно [2],

V v(x * ) = V u(x * ),    4 v(x * ) < 4 u(x * ).

Так как |V u(x * ) | ² = m ^ = ^л , то при a' <  0, a >  0 выполнено r ^{0 2}

>

-

2a0   я a,а

при a ' >  0, a >  0 , соответственно, r ^{0 2} >  0 .

Рассмотрим случай a ⁰ <  0, a > 0, r ⁰ >

C учетом (1), имеем:

/ 2a0"

^- a^.

Qm^(r) = ^Qv ^| _x= x , = ^div ⁽a^{( |}V v ^{| 2 )} V v^{) |} _x=x , = V a^{( |}V v ^{| 2 )} V v + a^{( |}V v ^{| 2 )} 4 v ^| _x=x , <

< V a( |V u | ² ) V u + a( |V u | ² ) 4 u | _x = x , = 0.

Откуда, в силу существования у функции r(t) в точке t непрерывных первой и второй производных, получаем нераве нств о (2).

Случай а' <  0, а > 0, Г <  -^^2 a ⁰ заменой в (7) m(r) на — m(r) и u(x) на — u(x) сводится к предыдущему.

Так как функция r(t) выпукла вниз и монотонна, то при а ' >  0, а >  0, —то < г ' <  то возможны следующие ситуации. Либо на интервале т ( F ) существуют два решения: для всех t <  t o выполнено r ' <  0 и для всех t >  t o выполнено r ' >  0 , где t ₀ — внутренняя точка интервала т ( F ) . В этом случае необходимо рассмотреть каждый интервал отдельно. Либо г ' <  0 (r ' >  0) на всем интервале т ( F ) . В обоих случаях приходим к неравенству (2).

Аналогичное дифференциальное неравенство для функции обхвата

n x2

i i=i /

1/2

в случае гиперповерхностей нулевой средней кривизны в R n ⁺¹ было получено в работе [3]:

P '' ^(t)     >  n - ¹

• ¹    + р '^{2 (t)} - p^(t) ’

а для гиперповерхностей трубчатого типа заданной средней кривизны – в [4]: пусть H(х) = H(x, t) — некоторая непрерывная функция и H(х) > 0. Положим H0(r, t) = minH(x,t). Пусть F — гиперповерхность трубчатого типа в Rn+1 с про-|x|=r екцией (а, в) на ось Ot. Предположим, что в каждой точке х € F средняя кривизна F неотрицательна и равна H(х). Тогда функция обхвата p(t) поверхности F выпукла вниз на (а, в) и почти всюду на (а, в) удовлетворяет дифференциальному неравенству

Р^ n— 1

(1 + p '² (t)) ^{3 / 2}     p(t)(1 + p '² (t)) ^{1 / 2} >      ^{O (P( ), ).}

Для минимальных поверхностей произвольной коразмерности данное неравенство получено сначала в [9], затем в уточненной форме – в [5], а для седловых гиперповерхностей заданной средней кривизны — в [8]. Подобное неравенство для гиперповерхностей постоянной средней кривизны было установлено в [10].

Основным результатом данной работы является следующая теорема.

Теорема 1. Пусть функция u € C ⁰ (Q \ Q ₀ ) П C ² (Q \ Q ₀ ) — решение уравнения (1),

выполнены усл о вия (i)–(ii) леммы 1 и

• (iii)    lim ^ sa(s) = А > 0 , где S — точная верхняя грань множества допустимых значений переменной s , при которых выполнены условия (i)–(ii).

Тогда r ₀ > 0 и

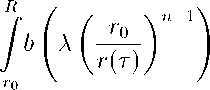
dr > | T — t 0 | ,

где b ( a ) = [ y Sa(s)] ¹

Доказательство. Для любого радиуса r существует точка x * Е S r : m(r) = u(x * ) .

² _a ^a , а при

Так как |V u(x * ) | ² = т Г ² = Г 2 , то при а' <  0, а >  0 выполнено r '² >  а' >  0, а >  0 , соответственно, r'" ² >  0 .

-

Рассмотрим случай а ' <  0, а >  0, г ' >    — 2 a 0 .

Так как по лемме 1 функция r(t) выпукла вниз, то ее производная r ' (t) возрастает. Кроме этого, r ' (t) >    — 2 a ⁰ > 0 , то есть возрастает и сама функция r(t) .

Таким образом, существует единственная точка t ₀ — крайняя левая точка интервала т ( F ) — в которой достигается наименьшее значение r ₀ .

Изучим сначала ситуацию, в которой r ₀ > 0 .

По лемме 2 функция r(t) удовлетворяет почти всюду неравенству (2), из которого получим

Функция

^r ' (^t)r"(t⁾ r '² (t)

— 2

ln а

/

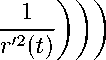
t

> 2(n — 1)

r ' (t) ^r(t)

> 0.              (8)

In ( г '² (т) ) + In а

1 г '² (т)

не убывает при t ≥ t ₀ , поэтому при всех τ ≥ t ₀ имеет место неравенство [6, с. 340]

ln

г '² (т) A r '² (t o )/

+ In

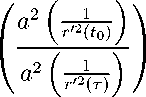
τ

>Л2

t 0

r ' (t)r '' (t) r '² (t)

— 2

In а r'2(t)         t

dt.

Отсюда, на основании соотношения (3), получаем откуда имеем

ln

r '² (т) А r ' ² (t o )/

+ In

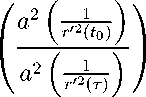
> (n — 1) In

≥ rn-1

r ² (т) r ² (t o )

r ' (т)

a r ^{0 2 1} ( τ )

^{(т )r} 0

r

n - 1 0

a

( V т >  t o ).

Покажем, что функция b(a) = [ д/ва (в)] ¹ существует. Действительно,

[ VNs^S =

а ( з ) 2 ^Ts

1 + 2s

а'( s ) А а ( з )

> 0.

То есть функция a(s) = ^а(⁵) монотонно возрастает и непрерывна (вследствие дифференцируемости а(в) ), следовательно обратная к ней монотонно возрастающая функция b(a) существует.

С учетом (iii) из (9) получим откуда

r'(т ) a ( r^

≥

r ^{n - 1} (T) rT^

( Vt >  t o ),

n-1

)>

V г ( т ) /     ) r ( t )

( V t >  t o ).

Интегрируя (10), получим

т(тг)               \n-A        T(Tr)

r o                    dr

J bl^Alr(7))   Г >J гй) =^{T - 10}

r 0                                          r 0

( V t >  t o ).

Соотношение (11) для t = T можно переписать в виде:

R

/ b(A

n - 1

4°v)     dr >  T — to.                     (12)

rv)

r 0

В случае a' <  0, a > 0, r ' <  -\j- 2 a ⁰ неравенство (12) примет вид:

n - 1 dr >  t o — T.                      (13)

rv)

R

/ b(A

r 0

Объединяя оценки (12) и (13), приходим к неравенству

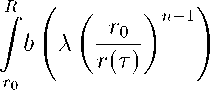
dr > | T — t o | .

Покажем, что r _o не обращается в ноль. Предположим противное. Тогда t _o может являться только левой концевой точкой промежутка t ( F ) . Зафиксируем произвольно точку t _o > t _o и рассмотрим поверхность F , отсекаемую от F гиперплоскостью n(t _o ) и расположенную в R ^{n +1} выше n(t _o ) . Наименьшее значение r e достигается в точке t _o . Воспользуемся неравенством (14) применительно к F . При любом t > t _o имеем

-

/^-^

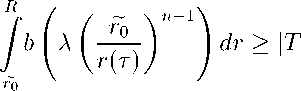
t o | .

Переходя здесь к пределу при t _o ^ t _o , получаем | T — t _o | <  0 , что невозможно.

Так как функция r(t) выпукла вниз и монотонна, то при a' > 0, a > 0, —то < r < то возможны следующие ситуации. Либо на интервале t(F) существуют два решения: для всех t < to выполнено r' < 0 и для всех t > to выполнено r > 0. В этом случае необходимо рассмотреть два интервала: t < t0 и to < t, где to — внутренняя точка интервала т(F), в которой достигается минимальное значение r0. Либо г' < 0 (r' > 0) на всем интервале т(F). Тогда точка минимума t0 — крайняя правая (левая) точка интервала т(F). В обоих случаях доказательство аналогично приведенному выше.

Аналогичная оценка для функции обхвата p(t) = max | x | была дана в [3]. x eE ( t )

В этой работе рассматривалась функция

z

Ф n (z) = I (s ²⁽ n ^{- 1)} - 1) ^{- 1 / 2} ds, 1

обратная к которой обозначалась Ф _п (t) . Было доказано, что в случае минимальной трубчатой гиперповерхности F в R ^{n +1} при всяком t Е т ( F ) выполнено

| t - t ₀IA

P ( t ) >  P 0 ^ n ------- ,

P0  / где p0 = inf p(t) — наименьший радиус обхвата поверхности F. Как следствие tEr (F)

данного неравенства в [3] приведен следующий факт: если F есть вложенная минимальная трубчатая гиперповерхность в R ^{n +1} , то

т ( F ) <  2р 0 Ф п ( ^ ).

В более общем случае, когда F — гиперповерхность в Rn+1, n > 3 трубчатого типа со средней кривизной H(х) > 0 в [4] было доказано, что для проекции (а, в) поверхности F на ось Ot выполнено в - а < 2р0Фп(то).

Примером уравнения, для которого условия теоремы 1 не выполнены, является уравнение максимальных поверхностей. Действительно,

(             1

a(s) = Гл----- 1-s и условия (i)-(ii) теоремы 1 выполнены при 0 < s < 1, но ^/sa(s) —> то. При этом 5^1

известно, что решение данного уравнения имеет изолированную особую точку.

Следствие 1. Пусть функция и Е C ⁰ (Q \{ x ₀ } ) П C ² (Q \{ x ₀ } ) — решение уравнения (1), выполнены условия (i)-(iii) теоремы 1 и u | _dQ = 0 . Тогда и = 0 .

Доказательство. Предположим противное, тогда в точке х ₀ достигается максимальное или минимальное значение функции u . Положим для определенности, что t ₀ = u(x ₀ ) > 0 — максимум. Проведем гиперплоскость n(t) , где 0 <  t < t ₀ (рис. 2).

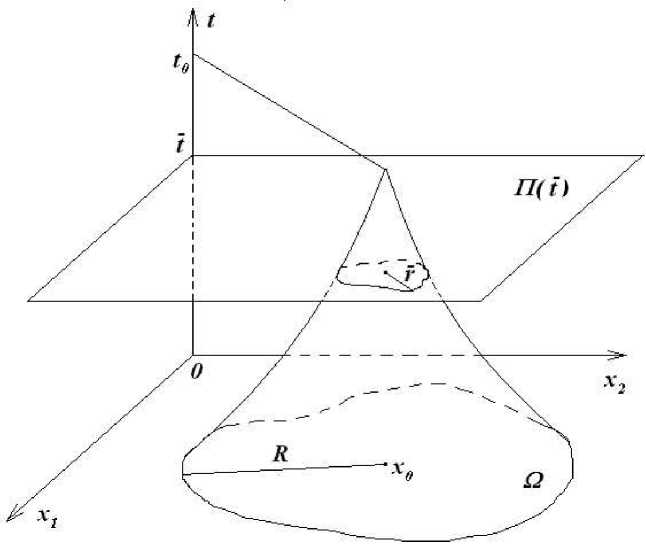
Рис. 2. Сечение поверхности F с R3 гиперплоскостью n(t)

Тогда

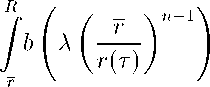
dr ≥ t, где r > 0 — радиус области, ограниченной сечением J2(t). Устремляя теперь t к t0, получим 0 > t0, что невозможно.

Автор выражает признательность А.А. Клячину за помощь в постановке задачи и подготовке данной статьи.