Об эффективности параллельных алгоритмов при моделировании динамики лесных пожаров

Известно негативное влияние природных пожаров на состояние окружающей среды. Так, одной из причин эффекта глобального потепления климата считают выбросы СО2 и других многочисленных газов, возникающих в результате пожаров [1–3]. Помимо влияния на климат Земли, лесные пожары наносят ущерб лесному фонду, а также способствуют возникновению таких катастроф, как большая задымленность больших городских территорий (например, в Москве в 2002 г.) или массовые городские пожары (например, в Лос-Аламосе (США) в 2002 г.).

Содержательный обзор исследований по проблеме моделирования процессов горения при лесных пожарах дан в работе [4]. Большой вклад в разрешение этой проблемы внесли Н. П. Курбатский, Э. Н. Валендик, М. А. Софронов, А. М. Гришин, Г. Н. Коровин, Р. Ротхермел, M. E. Aлександер и другие ученые.

Разработка математических моделей распространения пожара позволяет предсказать его поведение, что может способствовать более эффективному проведению противопожарных мероприятий. Однако ключевой проблемой при этом является необходимость сбора большого количества информации об условиях горения и противопожарных мероприятиях. В последнее время в связи с разработкой и вводом в эксплуатацию Информационной системы дистанционного мониторинга «ИСДМ-Рослесхоз» [5], основанной на использовании спутниковой информации о пожарной обстановке в лесах, сложились благоприятные условия для создания систем моделирования и прогнозирования лесных пожаров на всей территории Российской Федерации.

Следует отметить, что решение задач моделирования крупных многодневных лесных пожаров требует значительных вычислительных ресурсов, что может быть достигнуто за счет использования кластерных вычислительных систем. При этом получение равномерного распределения вычислительной нагрузки между процессорами связано с разделением вычислительной области на подобласти, количество которых совпадает с числом используемых процессоров, т. е. с применением принципа геометрической декомпозиции [6].

В данной статье рассмотрена разработка параллельного алгоритма, основанного на разбиении моделируемой области на равновеликие подобласти, и исследование его эффективности при использовании модели лесного пожара типа бегущей волны [3].

Разработка параллельных программ практического уровня сложности представляет собой многоэтапный технологический процесс, включающий постановку и анализ задачи, выбор модели программирования, декомпозицию задачи на параллельные процессы, анализ производительности и организацию вычислительного эксперимента.

Постановка задачи. В качестве базовой модели процесса распространения лесного пожара взята модель, основанная на вычислении теплового баланса в лесных горючих материалах [3]. Массив горючего в общем случае представляет собой n параллельных однородных слоев горючего, расположенных один над другим. Произвольный i -й слой занимает по вертикали область Z_i с координатами от z_iH до z_iK и содержит запас горючего материала ю ( x , y , z , t ) кг/ м 3 . Вертикальная координата середины i -го слоя обозначается z icp , а его толщина δ _i . При этом

_ ⁽ z iH ^+z iK )

z icP = ’

⁵ i = ^z iK ^- z iH , i = 1, K , n.

Свойства горючего в пределах каждого слоя не зависят от z.

Горючий материал в окрестностях точки C в некоторый момент времени может находиться в одном из трех состояний, описываемых функцией S ( x , y , z , t ) :

0, если в точке C в момент t

S ( x , y , z , t ) = <

имеется ненулевой запас горючего, т. е. ю ( X, y, z, t) > 0, но горения не происходит, 1, если ю ( X, y, z, t) > 0 и горение происходит, 2, если ю ( X, y, z, t) = 0 и горение невозможно.

Области, соответствующие состояниям S = 0, S = 1, S = 2, обозначаются соответственно Q 0 , ^ 1 , ^ 2 ■ Проекции областей Q _o, Q i , Q 2 на горизонтальную плоскость D будем обозначать соответственно D ₀ , D ₁ , D ₂ , причем D 0 и D i и D 2 = D .

Уравнение нагрева для горючего в окрестности точки C = (x, y, z), которое в момент времени t находится в состоянии S (x, y, z, t) = 0, имеет вид dHj (x, y, t) _ dt

= 1L Ц^ф i ( x i , y i , t ) ^ ij ( x i = 1 D i i

- x i , y - y i ) dx i dy i +

+ ^ф e ( x , У , t )^- k j ( x , У ) [ H j ( x , У , t )^- H 0 j ( x , y ) ], (1)

1     zjK где Hj (x,y, t) =----------- [ Hv (x,y,z,t)dz при на- zjK — zjH z H чальном условии Hj (x, y, 0) = Hоj (x, y), (x, У ) е Do j, i = 1,..., n, здесь Hv (x, y, z, t) - значение энтальпии в точке (x, y, z) в момент времени t; Ф , Фe - энергия, образующаяся при горении и поступающая от внешних источников соответственно, Вт/м3; ^j (x - x1, y - У1) -функция влияния пламени из точки (xi,У1) на точку (x, y) (функция Грина) из i-го слоя на j-й слой; k (x, y, z ) = —, здесь а - коэффициент теплоотдачи, Р c

Вт/(м² - град), 5 - удельная поверхность слоя, м^-1, c - приведенная теплоемкость влажного материала, Дж/(кг ■ град).

Условие воспламенения горючего в j -м слое, т. е. перехода горючего в состояние S j ( x , y , z , t ) = 1, имеет вид H j ( x , у , t *j ) >  H ^j ( x , y ) , где t * = t * ( x , y ) - время воспламенения горючего в j- м слое в точке ( x , y ) е D o j ; H - энтальпия начала газификации.

Уравнение расходования горючего будет следующим:

d to j ( x , У , t ) a t [ ^to0 j ( ^x , у )

- r j при to j ( x , y , t ) > 0, = <

0 при to j ( x , y , t ) = 0

с начальным условием to j ( x , y , t * ) = to 0 j ( x , y ) , ( x , y ) e D 1 j . Здесь to j - активный запас горючего материала в j -м слое, кг/м³; r j - относительная скорость сгорания j -го слоя, с^-1.

Уравнение тепловыделения в j-м слое представим в виде

, х , х dto j ( x , y , t )

^Ф j ( ^x , у , t ) = ^- h j ( ^x , y )----- d t-----’

( ^x , У )^е D i j , j = 1,..., n ,                  (3)

где h j - теплота сгорания горючего, Дж/кг.

Условие погасания (перехода в состояние S j ( x , y , t ) = 2)

to j ( x , y , t j j ) = 0, ( ^x , y )^e D 2 j , j = 1,..., n .

Модель теплопередачи из зоны горения к горючим материалам, задаваемая функцией влияния (функцией Грина) ^ j ( x - x 1 , y - У 1 ) , подробно рассмотрена в [3].

Система уравнений (1)...(3) представляет собой мо- дель процесса распространения горения по неоднородным слоям горючего типа бегущей волны. Особенностью этой модели является то, что часть входных и выходных переменных представляет собой множества Q0 (t), Q1 (t) и Q2 (t).

Метод решения. Рассмотрим алгоритм построения горящей кромки, основанный на численном решении уравнений, описывающих распространение процесса горения. Введя в каждом из слоев прямоугольную сетку с шагами Ax и Ау по координатам x и у соответственно, заменим области D0i , D1i и D2i соответствующими сеточными областями DА0i, DА1 i, DA2i, i = 1, 2. Перейдем к дискретному времени, рассматривая систему в моменты t = 0,1, 2,... с шагом At. Заменив в (1), (2) час- тную производную по времени разностными отношениями, а интеграл по области D1i суммой, получим следу- ющее уравнение нагрева:

He (i, j, t +1) = He (i, j, t) + A t Ax Ay x xE S   Ф(m,n,t)x^si(m-i,n-j)+ s=1 (m, n )eD15

^+Ф el ( i , ^j , t )^A t ^{-A tk} l ( i , ^j )^{x x} [ H l ( i , ^j , t )^- H 0 1 ( i , ^j ) ]

с начальными условиями H i ( i , j ,0 ) = H 0 1 ( i , j ) , ( i , j ) e D A 0 1 , l = 1,2.

Условие воспламенения горючего в l -м слое при

Hl (i,j, t * )> Hj (i,j), узел (i, j) исключается из DA0i (t*) и присоединяется к j

D A 1 1 ( t ) .

Уравнение расходования горючего имеет вид tol (i, j, t +1) =

[to l ( i , j , t ) - r l A t при to l ( i , j , t ) > 0,          ⁽⁵⁾

[ to l ( i , j , t ) при to l ( i , j , t ) < 0

с начальным условием ^to l ( i , ^j , t ) = ^to0 1 ( i , ^j ) , ( i , j ) е D A 1 1 , l = 1, 2, а уравнение тепловыделения - вид

^Ф l ( i , ^j , t ) = ^- h l ( i , ^j )^x _x[ ^to l ( i , j , t )^{- to} l ( i , j , t ^-A t ) ]

A t

,

( i , j ) е D A 1 1 , l = 1,2.                    (6)

Условие погасания при t = t *

to l (i,j, tj ) = ° (i,j )e DA11, точка (i, j) исключается из Da1 i (t*) и присоединяется к DA21 ( tj ).

Функции влияния ^ iij ( x - x 1 , y - У 1 ) зависят от характеристик леса, природных и погодных факторов и вычисляются по специальным подпрограммам [3].

Используем следующие исходные данные:

• -    область моделирования в виде двух множеств узлов ^D a l = { ( i , ^j ) , i = ¹ ,-, n l , ^j = ¹ ,-, m l } , l = 1,2;

• -    начальный и конечный моменты времени 1 0 и t f , временной шаг A t ;

• -    участки с одинаковыми характеристиками горючих материалов Q kl , k = 1,..., K , U Q kl = D _A l , l = 1, 2;

• -    теплофизические характеристики горючего для каждого из участков Q kl в каждый момент времени: ^H 0 kl ⁽ t ) , ^H kl ( t ) , ^k kl ⁽ t ) , h kl ⁽ t ) , ^to0 kl , ^Ф ekl ⁽ t ) , ^to l ( i , ^j , t ) , l = 1,2, k = 1,..., K , t = t 0 , t 0 + ^A t ,..., t f ^;

• -    параметры функции, описывающей тепловое воздействие локального пламени Р 0 kl ( t ) , a 0 kl ( t ) , 5 kl ( t ) , h fkl ( t ) , ф ь ( t ) , w ( t ) ;

• -    скорости сгорания r kl ( t ) для всех участков Q k в каждый момент времени t = 1 0 , 1 0 +A t ,..., t f , k = 1,..., K ;

• -    начальное состояние системы - области D А 0 i ( 1 0 ) , D A 1 1 ⁽ t 0 ) , ^D A 2 1 ⁽ t 0 ) .

Используя информацию о лесном горючем и внешней среде, можно получить исходные данные для рассматриваемой модели. Наибольшую сложность представляет вычисление функции влияния пламени Еф- (x - Xi, y - y). При моделировании крупных многодневных пожаров оценку этой функции также можно получить путем анализа аэрокосмических снимков пожара, полученных в последовательные моменты времени (рис. 1). На основе этих снимков могут быть вычислены необходимые для расчетов значения функций Еф (x - Xi, y - yi) и скоростей. Поскольку конфигурация кромки реальных пожаров часто является достаточно сложной, то для упрощения расчетов целесообразно применять сглаживание границы контура на снимке пожара, например его аппроксимацию эллипсом [3]. Это позволяет оперативно получать необходимые для моделиро- вания исходные данные.

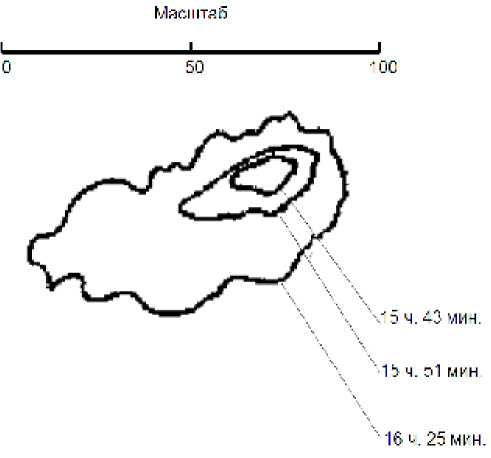
Рис. 1. Динамика контуров пожара

Распараллеливание вычислений. Для распараллеливания процесса вычислений предлагается схема, вытекающая из физического содержания данной задачи. Расчет энтальпии для точки ( i , j ) на ( t + 1)-м временном шаге происходит с использованием некоторого количества точек на t -м шаге. Численный расчет ведется итеративно: по имеющимся значениям t -го временного шага выстраивается ( t + 1)-й шаг и т. д. Таким образом, исходную задачу можно разбить на p подзадач для областей D Д 1 i , D Д 2 i , D Д з i , l = 1, 2, k = 1,..., p , пересекающихся только по границе разбиений и независимых друг от друга на каждом расчетном шаге.

В случае использования технологии MPI каждый процессор получает часть сетки, причем сетки соседних процессоров пересекаются по двум узлам. Это пересечение позволяет частично продублировать вычисления на соседних процессорах, что сокращает межпроцессорные обмены. Затем каждый процессор последовательно на каждом шаге по времени проводит вычисления на своей части сетки. И на каждом шаге по времени соседние процессоры осуществляют обмен граничными значениями при помощи функций неблокирующих пересылок и при- ема данных MPI_Isend и MPI_Irecv. По окончании расчетов каждый процессор обрабатывает свой массив вычисленных значений, записывая его в отдельный файл.

Сбалансированность вычислений и минимизация межпроцессорных обменов может быть обеспечена за счет выбора оптимального способа распределения данных и вычислений по процессорам. В рассматриваемом нами случае возможны два способа разбиения исходной области по вычислительным узлам: одномерное (на полосы) и двумерное (на квадраты).

В обоих случаях исходная область включает взаимно перекрывающиеся подобласти, и пересчет значений на границах между ними согласно алгоритму, предполагает суммирование при обмене вычисленными значениями для граничных элементов. При этом для перехода к следующей итерации необходимо согласование значений на границах расчетных подобластей. Пересылка данных осуществляется с использованием процедур библиотеки MPI [7–9].

Определим теперь потенциальное ускорение алгоритма. Будем оценивать время работы параллельной программы исходя из соотношения S p = T j / T p , где S p -ускорение; T ₁ – время вычислений на одном процессоре; T_p – время вычислений на p процессорах.

Для получения реалистичных оценок, помимо классической формулы Амдала [6], будем учитывать также время, затрачиваемое программой на обмены между процессами. Как следует из принятой нами схемы распределения данных, на каждом временном шаге требуется обмен границами. Время пересылок для различных способов декомпозиции можно приблизительно выразить через количество пересылаемых данных [6]:

1 D 3

V comm = 2 ■ N ■ т при одномерном разбиении,

V2Dcomm = ""4" ■ N3 ■ т при двумерном разбиении, p где N3 – размерность задачи; p– количество вычислительных узлов; τ – время пересылки одного числа. Алгоритм и его программная реализация являются масштабируемыми, если ускорение и производительность линейно зависят от количества используемых процессоров [6; 9]: Sp = O(p). На практике алгоритмы, для которых Sp = O (p /(ln p)), также считаются масштабируемыми.

Проведение вычислительного эксперимента и анализ результатов. Параллельные программы тестировались на модельной задаче, для которой был выбран один однородный слой горючего, расположенный на местности с уклоном, изменяемым по заданному закону.

Расчеты проводились по формулам (4)...(6) на кластерной системе МВС 1000 Института вычислительного моделирования Сибирского отделения Российской академии наук (ИВМ СО РАН) на тестовой сетке 400 х 400 узлов при использовании от одного до шестнадцати процессоров.

Тестовая область Q представляла квадрат Q = [1,6п] х [1,6п]. Возвышение поверхности задавалось косинусоидой z(x) = 1 + cos(x /150). Процесс распространения пожара инициировался из узла с координатами (0,5; 0,5). При запуске параллельных программ измерялось время их работы в секундах. На основе данных о времени работы параллельных программ определялись другие их характеристики, такие как ускорение и эффективность распараллеливания (табл. 1). В вычислительных экспериментах было сделано по 100 шагов по времени.

Анализ данных табл. 1 показывает, что при применении двумерной декомпозиции и восьми процессоров значение эффективности больше единицы, что объясняется использованием в программе динамических массивов с подстраиваемыми под выделенное число процессоров размерами. Таким образом, временные затраты на выборку обрабатываемых данных из оперативной памяти и их передачу через кеш-память уменьшаются. В случае использования восьми процессоров при данной размерности сетки весь массив помещается в кеш-памя-ти, что и определяет более быстрое выполнение вычислений за счет отсутствия необходимости обмена между оперативной и кеш-памятью.

Полученные в результате вычислительного эксперимента графики зависимости ускорения алгоритмов в зависимости от количества используемых процессоров (рис. 2) показали наличие хорошего ускорения при решении модельной задачи.

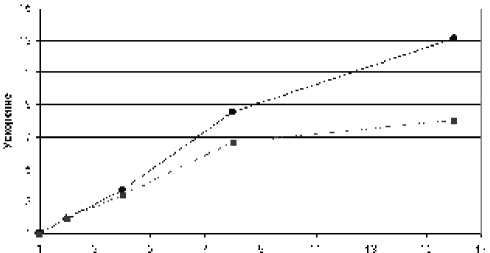
Количество процессоров

—•— Ускорение при двумерном разбиении — ■•— ускорение при линейном разбиении

Рис. 2. Зависимость ускорения от количества доступных процессоров

Также был проведен вычислительный эксперимент по выявлению зависимости ускорения вычислений от роста размерности задачи. Были рассмотрены случаи мелкой (10 000 узлов) и крупной (640 000 узлов) сетки. Тестовая область Q представляла, как и ранее, квадрат Q = [1,6п] х [1,6п], а возвышение поверхности задавалось косинусоидой z(x) = 1 + cos(x /150). Характеристики горючего не изменялись. В вычислительных экспериментах было сделано также по 100 шагов по времени. Декомпозиция расчетной области – двумерная. Полученные значения ускорения и эффективности, показанные на кластере ИВМ СО РАН, приведены в табл. 2.

Выполненные расчеты позволяют сделать вывод, что с увеличением размерности задачи при использовании четырех процессоров наблюдается увеличение ускорения вычислений. По крайней мере, для задач размерностью не более 800 х 800 при учете размера кеш-памяти можно добиться эффективности больше 1.

Значения ускорения вычислений с увеличением размерности задачи при использовании двумерной декомпозиции расчетной области возрастают логарифмически (рис. 3). Эту зависимость можно аппроксимировать выражением y = 0,3151ln( x ) - 0,205 9 с достоверностью аппроксимации R ² = 0,8821.

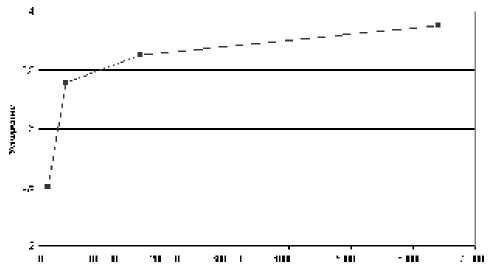
Размерность задачи

Рис. 3. Зависимость ускорения алгоритмов от размерности задачи

Таким образом, при увеличении размерности задачи в 4 раза ускорение вычислений при использовании четырех процессоров возрастает. Средний уровень эффективности распараллеливания составляет около 83 %, что связано с неизбежными затратами времени на организацию межпроцессорных обменов и записи результатов в файл.

Итак, при численном решении задачи моделирования динамики лесного пожара возможно применение как одномерной, так и двумерной декомпозиции. Однако тестирование программ показало, что наиболее эффектив-

Таблица 1

Значения ускорения алгоритмов и эффективности распараллеливания в зависимости от количества используемых процессоров

Характеристики параллельных программ	Количество процессоров
	1	2	4	8	16
Двумерное разбиение расчетной области
Время выполнения основного цикла T ,c	700,868 934	359,845 6	188,142 001	81,975 424	53,299 19
Ускорение S	1,000 000	1,947 693	3,725 213	8,549 745	13,149 71
Эффективность E = S / p	1,000 000	0,973 847	0,931 303	1,068 718	0,821 857
Одномерное разбиение р асчетной обл асти
Время выполнения основного цикла T ,c	700,868 934	359,8456	207,077 7	105,259 7	87,268 06
Ускорение S	1,000 000	1,947 693	3,384 569	6,658 474	8,031 219
Эффективность E = S / p	1,000 000	0,973 847	0,846 142	0,832 309	0,501 951

ным при использовании, по крайней мере, от четырех до шестнадцати процессоров является двумерное разбиение исходной области.

В результате исследования были созданы следующие программы:

• –    программа, решающая обратную задачу получения значений скоростей на основе аэрокосмических снимков контуров пожара в последовательные моменты времени;

• –    программа для препроцессорной обработки данных – разрезания данных на отдельные файлы для многопроцессорных вычислений;

• –    программа для численного моделирования распространения кромки лесного пожара.

Также были рассчитаны значения ускорений, позволяющие оценить масштабируемость алгоритма и его программной реализации. Эти значения показывают, что алгоритм обладает значительным объемом потенциального параллелизма и хорошей (с точки зрения распараллеливания) структурой, что позволяет надеяться на получение ускорений, близких к линейным в зависимости от количества процессоров, используемых для кластерных вычислительных систем. Значения ускорений, полученные в ходе вычислительного эксперимента, хорошо согласуются с теоретическими оценками.