Об эволюционных уравнениях задач ударного деформирования с плоскими поверхностями разрывов

строить численные решения только на основе методов расчетов, применяемых в газовой динамике [3–4]. Таким образом, решение задач ударного деформирования в твердом теле при необходимости четкого выделения поверхностей разрывов требует разработки новых приближенных методов вычислений.

Один из таких методов, используемый в настоящее время [5–7] и находящийся в стадии разработки, основан на объединении приближенного аналитического представления решения в прифронтовой области ударной волны и конечно-разностных методов расчетов в остальной области деформирования. Решение в прифронтовой области находится либо лучевым методом (вариант для ударных волн) [8–10], либо методом сращиваемых асимптотических разложений [11–12, 14–15].

Лучевые ряды имеют сравнительно простую структуру, в частности, их зависимость от времени носит степенной характер. В результате краевые условия задачи тоже должны быть выражены степенными функциями, а это накладывает на них серьезные ограничения. Более того, учет в лучевых рядах слагаемых выше квадратичных возможен только при многократном применении процедуры метода, которая сама по себе связана с большим числом громоздких вычислений.

В этом смысле метод сращиваемых асимптотических разложений можно считать более эффективным. На простом примере плоских одномерных процессов в работах [13–15] показано, что прифронтовая область ударных волн определяется некоторым эволюционным уравнением первого порядка. В частности, для плоских продольных ударных волн таким уравнением является известное уравнение Хопфа [16]. Для поперечных волновых процессов в несжимаемых средах прифронтовая область волны также описывается эволюционным уравнением [17], в котором угол наклона характеристик зависит от квадрата строящегося решения.

Ранее [14, 17] решения эволюционных уравнений рассматривались для простых краевых условий в пределах линейной и квадратичной зависимостей от времени. В настоящей статье обобщение методики сращиваемых асимптотических разложений распространяется на краевые условия, задаваемые в виде произвольных функций времени. Суть подхода излагается на примерах плоской продольной волны в сжимаемом упругом полупространстве и поперечной плоской волны в несжимаемом полупространстве.

• 2.    Общие модельные соотношения и условия на ударных волнах

Движение нелинейно-упругой изотропной среды в декартовой пространственной системе координат x_t ( i = 1,2,3 ) в представлении Эйлера определяется общей системой уравнений:

vi = u i + ui j v j , ^2a у = uu + j - uk, i u k j ,

P 9 W

• ayj Plvi + vV), aу = —     (5kj - 2aу),

^p O ^da ik

W = ^ 1 2 +ц 1 2 + lI 1 1 2 + hi 3 + zi 3 +^ 1 2 ++n 1 2 1 2 +K 1 1 1 3 +x I !4 + ^ ,

• 1 1 = ^a ii ,    ¹ 2 =^a ij ^a ji ,    ¹ 3 = ^a j ^a jk ^a ki ,

  5 u,.

  ^u , j=     ’

  d x j

  
  

  u i =

  
  

  du i ”tT ,

  
  

где ui и vi — компоненты векторов перемещений и скорости среды; aj — компоненты тензора деформаций Альманси; aj — компоненты тензора напряжений Эйлера-Коши;

р и р ₀ — плотность среды в текущем и свободном состоянии; W — упругий потенциал; X , ц , l , h , z , ^ , п , к , % — упругие модули, первые два из которых — параметры Ламе; 5 j — символы Кронекера. В формулах (1) и далее индексы i , j , к принимают значения 1, 2, 3; суммирование проводится по повторяющемуся индексу; многоточием обозначаются незаписанные слагаемые с более высоким порядком малости.

Если предметом изучения является только сдвиговое деформирование, то используем наиболее простую модель — нелинейно-упругий несжимаемый изотропный материал. В этом случае связь деформаций и напряжений устанавливается формулами

С j    P5 ij + da (5 kj 2a kj ),

W = (a - p) 11 + al2 + bi2 - kI112 - 0113 + ci4 + di2 + 311212 + - которыми далее заменяются соответствующие уравнения в системе (1). В выражениях (2) приняты обозначения: P — величина добавочного гидростатического давления, p, a, b, к, 0, c, d, 3 — упругие модули среды.

Если краевые условия приводят к возникновению ударных волн, то на них, вследствие интегральных законов сохранения, должны выполняться динамические условия совместности разрывов [18], а также геометрические и кинематические условия совместности [19]:

[р( vjnj- G )] = 0,

[°,]nj =р+(v+nj- G)[V],

^{[ L}. i ]= f n i ⁺ a “ ^{P [ L} l a Х в

= р+( vj'nj- G ){ЦИ [ LLML.

^{+ [} e ^]H q^ n j ,

dn

5 1 ’

a a_P = x i , a xi$, ,     a “ ⁷ a _yp = ⁵ a ,     ⁿ i n i = 1,     ⁿ i x i , a = ⁰,

X'«=7xa- -   dr = f,n •   [ L ] = L *-L - (“ = !'2' e = !'2' Y = 1.2)• dy     dn где e — плотность распределения внутренней энергии; qj — компоненты вектора теплового потока; ni — компоненты единичной внешней нормали к поверхности ударной волны S, направленной в сторону движения волны; G — скорость ударной волны в направлении нормали; у“ — поверхностные координаты; aa₽ — ковариантные компоненты поверхностного метрического тензора; индексы «+» и «-» обозначают предельные значения разрывной величины перед поверхностью S и за ней соответственно; квадратными скобками обозначен разрыв величины, заключенной в них. Также в (3) 5 / 51 — производная Томаса [19] по времени в данной точке поверхности S (дельта-производная).

• 3.    Задача о плоской продольной ударной волне

Рассмотрим нелинейно-упругое изотропное полупространство х1 > 0, которое до момента времени t = 0 считаем недеформированным. Начиная с t = 0, на границе х1 = 0 под действием нагрузки создается известное перемещение и1\ Х1 = g(t) — g (t), g (0)— 0, g' (0)> 0, t >0

причем все используемые далее варианты функции g ( t ) приводят к мгновенному образованию ударной волны. В среде возникает поле перемещений и — и₁ ( x₁, t ) , и 2 — и 3 = 0 . На поверхности чисто продольной ударной волны S с учетом уравнений (3) имеем:

и|         — 0, т —ГU 1 г

¹ x i ^—J 6 1 ⁽ g ) dg                     L ^,1 J| x 1 — J G 1 ( g ) dg

G1 — C^1 + P1T + P2T2 + .,

о 9 J + h + zPi —     3,1 2    X + 2ц

Cl — ^(X + 2ЩР.

в2 — 8 -15 l+LH + 4 K + X + n+;

X + 2ц      X + 2ц

Система уравнений (1) сводится для поставленной задачи к уравнению движения Навье

^u ,11 ( 1^{+ a} 1 ^u ,1 )+.

— C 1 { u ( 1 — 2 U 1 ) + 2 U 1 u } +. „ ,

a1

—9 + 6

l + r + zX + 2ц

— —2P1.

Чтобы применить метод сращиваемых асимптотических разложений к краевой задаче (4–6), определим следующие безразмерные переменные:

x ₁

C 1 T

t

т — —, T

w (5, т)

£

- 1

и ( x1, t)

C 1 T

£ « 1,

где T — характерный масштаб времени, £ — малый параметр. К примеру, положим, что £ — g' (0) C1—1, если g ‘( 0)> 0. Учитывая переменные (7), перейдем от условия (4) к условию w (5, m )| 5 —£f (т) — f (m) ,  w (5, m)| m<о — 0,

т > 0

где функция f соответствует функции g ( t ) , записанной в переменных (7), а вместо уравнения (6) получим уравнение

w„ 11 + £a,ну ) + . — wmm (1 — 2£ну ) + 2£w„w,_ + . .

, ss            1, s                , mm              , s            , m , sm         .

Для решения уравнения (9) представим функцию w ( 5 , т ) как степенной ряд вида:

w(5, т) — w0 (5, т) + £w1 (5, т) + £2w2 (5, т) + ., где многоточием обозначены незаписанные слагаемые с более высокой степенью малости по параметру £ .

Последовательно подставляя ряд (10) в уравнения (8), (9), методом линейных приближений определим решение, называемое внешним [12]:

w (s, m) = f (0 + s|-51 ( f '(У )2 s + f '(^) f (У+ s2|^ (f' (S))2 f ’(У s2 -—a Ь+5 )■ f ’®)3s-a f ® f'® f *<0$+2 (• f <9)2 f чэ +           (id

41+11)(f,(S))2 f (S)>+-,      S=m — s.

При построении данного решения не учитывалось краевое условие (5). Для его учета необходимо построить дополнительное, внутреннее [12], разложение решения в области неравномерности исходного ряда (11). По пространственной координате такая неравномерность появляется на расстояниях, где s ~ s^{— 1}. Поэтому новыми независимыми переменными для внутренней задачи [12] выберем следующие: n = s s , p = s — m .

От уравнения (9) перейем к уравнению

( Wpp + 2sWnp + s2W,nn ){1 + sai ( Wp + sWn ) I + -  wpp {1 — 2s( wp + sWn )} + 2swp ( Wpp + swnp ) + -, причем новую искомую функцию внутреннего решения wi = w (n, p) также представим в виде ряда по степеням малого параметра s . На нулевом шаге получим хорошо известное эволюционное уравнение v0,n + 2 а1 v0v0,p = 0 ,

v 0 = ^W 0, p ,

называемое уравнением Хопфа [14]. Его общее решение имеет вид

1I v 0 = F I 2 ^a i v 0 n ^— p l ,

где функция F определяется краевыми условиями в области, пограничной для внешнего и внутреннего решений, то есть при l = s k s ( 0 <  k <  1 ) .

Сравнение решений (11) и (13) на нулевом шаге дает равенство F = — f '. Для функции f произвольного вида укажем два способа решения уравнения (13): параметрический (носящий более универсальный характер) и явный. С учетом того, что v о = w _{0 p} , уравнение (13) является обыкновенным дифференциальным уравнением относительно функции w ₀ . В нем p — независимая переменная, а координата n играет роль параметра. Это уравнение не содержит искомой функции, поэтому его решение удобно искать в параметрическом виде. В пространстве переменных n , p , y имеем:

у = ^{0,5 a} 1 nv 0 ^— p ,    v 0 = ^F ( У ) ,    p = p ( y , n ) = ^{0,5 a} 1 nF ( y ) ^— y .

Отсюда следует решение в параметрическом виде:

W 0 ( У , n ) = ^0,25а 1 nF ² ( У ) + ^f ( У ) + V o ( ⁿ ) ,

• p ( У , ⁿ ) = ^-0,5а 1 nf'У ^- У ,     F ( У ) = ^- f ' ( У ) ,                                   (14)

_ w0 ( p, n ) = wo (p ( У, n ), n ) = Wo ( У, n ) , где v0 (n) — пока не определенная функция.

Условие (5) и уравнение эйконала в переменных внутренней области приводят к уравнению

1 - 2 8 dp + 8 = dn

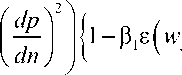
^{+ 8} w n ) + p 2 ⁸ 2 ( w p

+ 8 W n ) + ^ } = 1,

в котором функция p ( n ) связывает независимые переменные на ударной волне S . Для его решения зададим положение ударной волны парой функций n ( у ) , p ( у , n ( у ) ) и учтем соотношения (14). Неизвестную функцию n ( у ) также представим в виде ряда по степеням малого параметра n ( у ) = n ₀ ( у ) + 8 n 1 ( у ) +... . В результате на нулевом шаге метода из уравнения (15) получим уравнения, определяющие положение волны S :

<

p о ( У ) = p ( У , ⁿ о ( У ) ) = ² f ^y n ₍ у ) = - ± f ⁽ У ) ⁰           “ 1 ( f '( у ) ) = .

y ,

Из них легко находится входящая в решение (14) функция: у ₀ ( n ) = 0 . На этом нулевой шаг внутреннего решения заканчивается.

Сопоставление внутреннего и внешнего решений в пограничной области показывает, что один внутренний шаг соответствует двум внешним.

Теперь остановимся несколько подробнее на построении приближений высших порядков. Для функции следующего шага w1 (n, p) из уравнения Навье для внутренней области имеем соотношение а,           а, а + 2            W0 nn  /                  ~ v1,n + 2^" W0,pv1,p + 2^" W0,ppv1 + ^2— W0,ppw0,n + -у- + (а1 - 1) W0,pw0,np = 0, v1 = w1, p, от которого также перейдем к уравнению с независимыми переменными y, n. Отметим, что уравнение (17) имеет такие же характеристические направления dp = 0,5а1 v0dn , как и исходное уравнение (12), поэтому вид зависимости p = p (у, n) из системы (14) сохраняется и здесь. Отсюда определим неявную функцию у (n, p) и ее частные производные:

,    ^a1f      _х , у. =¹_______ .

2 ( 1 + 0,5 а , nf ' )     ^{, p}    1 + 0,5 а ₁ nf"

С их учетом от уравнения (17) придем к уравнению

, _      «1 f•    „.Га2 «1) (fiV"

v 1 ( n , p ( y , n ) ) ^— V ( n , y ) ,

V +

1, ⁿ     2 ( 1 + 0,5 a , nf ") ¹ ( 2    4 J 1 + 0,5 a 1 nf"

в котором переменная y уже играет роль параметра. В результате интегрирования этого уравнения найдем:

2 - ^( fT nf" + K0 (y)            <2

V (n,y)— 1 2 4 J a------------, W (n,y)—    -^У-^ + K1 (y) + Vi(n

1 + ^a nf"                     V ^{2 4} J ³

где K 0 ( y ) , K 1 ( y ) и y 1 ( n ) — пока не известные функции. Из сравнения решений в пограничной области следует, что K 1 ( y ) — f ' ( y ) f ( y ) . Сопоставление внутреннего и внешнего решений показывает, что внутреннее решение более информативно, чем внешнее, поскольку двум его функциям W ₀ и W ₁ отвечают три функции внешнего ряда, то есть w ₀ ( 5 , m ) , w 1 ( 5 , m ) , w ₂ ( 5 , m ) .

Неизвестная функция у 1 ( n ) может быть определена только из условия нулевых перемещений на уточненном фронте ударной волны, где n ( y ) — n ₀ ( y ) + £ n 1 ( y ) . Из уравнения (15) для функции n 1 ( y ) получим решение:

L^A-A.;.'6в. 5.4 8е n1 (y) A1 f(f')2 1 (' (^)) d^ A1 3 + a2 , A2 2 + а1 а2 .

Тогда функция v 1 ( n ) находится из условия

Wo (n, y) + £ W (n, y )|           — 0.

0 3                     13 n '\n — n ₀ ( y ) +e n 1 ( y )

w

2 m ³²

2 m ³² —------

5 —£-----

,

AT ¹²

£ —----

C 1

.

В этом случае решение для внутренней области примет форму:

a,       / a2 2 „ n -J   n 2 - 4 p

vo (n, p) = -------2----------

1             a w (n, p )=4 ia np+3 I   n - 4 p

л 32 1

* + Vo ( n ),

где v0 (n) — пока не определенная функция. Зададим положение переднего фронта то ударной волны функцией вида: p (n) ~ ^ pk (n )аk . Тогда на нулевом шаге уравнение для к=0

определения функции p 0 ( n ) будет следующим:

^dpo ^ai   /      /

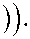
= V v 0 ( n, p 0 ( n dn 4

Проинтегрировав уравнение (19) с учетом формул (18) и условия p ₀ ( 0 ) = 0, получим p ₀ ( n ) = 3 a 2 n ² / 64. Подстановка найденной функции p ₀ ( n ) в краевое условие w₀ ( n , p ₀ ( n ) ) = 0 дает итоговый результат:

w0(n,p)=

a. 1 np 1 f a 2 n ²

+ 12 ("T"

4 p

a 3 n

Построение решения может продолжаться с определением на последующих шагах функций w_z ( n , p ) , p_z ( n ) , i >  1. Рассмотренное решение соответствует ситуации, когда в начальный момент времени интенсивность волны нулевая, но наличие вертикальной касательной в нулевой точке графика g ' ( t ) свидетельствует о мгновенном образовании ударной волны. Отметим, что сама функция g ( t ) в окрестности нуля не может быть представлена рядом Тейлора, что является стандартным приемом в работах [7, 10, 14, 17], но это не мешает определению решения во внутренней области на основе эволюционного уравнения.

Учет нелинейности, даже если она считается слабой, оказывает серьезное влияние на искажение функций, задающих исходное воздействие. Рассмотрим это свойство на примере еще одного краевого условия, считая, что в формулах (8)

f ( m ) = L 1 m + B 1 m ² + D 1 m 3 .

где L1,B1,D1 — константы. Для него на основе общего внутреннего решения уравнения (12) выберем частное решение в виде неявной зависимости v0 = L + B(p - 0,5a1 v0n) + D(p - 0,5a1 v0n) ,

где константы L , B , D пока не согласованы с константами краевого условия (20). Из (21) определим явную функцию v 0 ( p , n ) и соответствующую ей w ₀ ( p , n ) :

wn (p, n ) =,2 . , 0           3a3 D2 n3

fa ² 2 „   2

1 + a 1 Bn + 2 D a 1 pn + —B ² - DL a 2

+——^-(aj Bn p + D a p ² n + 2 p^ + v₀ ( n ) . a 2 Dn ²

2 n

+

Здесь v ₀ ( n ) — неопределенная функция. Обратим внимание на то, что функция (22) определена всюду, за исключением n = 0. В окрестности нуля для нее выполняется 23

условие lim w ₀ ( n , p ) = Lp + Bp- + Dp- , вследствие чего решение (22) доопределяется n ^ 0 0                     2       3

предельным значением в нуле. Очевидно, что граничные условия в перемещениях и их производные по времени воспроизводятся без искажения только в области малых значений переменной n . В области, где n ∼ 1, решение, задаваемое формулой (22), показывает искажение исходной временной зависимости. Действительно, от степеней t с первой по третью в формуле (20) приходим в полученном выше решении к степеням 1,32,2.

Положение фронта ударной волны в исследуемой задаче определяется неявной зависимостью, получающейся из решения уравнения (19):

313-{-3E2n4 + 6E (h2 -1)n2 - (h -1)3 (3h +1)} - 2Ea1 B + ^a3B3 = 0, h (n) = 1 + a1 Bn + 2a1 Dpn + En2, E = 0,25a2B2 - a12DA,

Эта зависимость стала основой для численного расчета положения фронта ударной волны (Рис. а ) и неизвестной функции v ₀ ( n ) , входящей в уравнения (22) для поля перемещений (Рис. б ).

Сравнение решений для внутренней и внешней областей позволило уточнить неизвестные константы: L = - L 1 , B = 2 B 1 , D = - 3 D 1 .

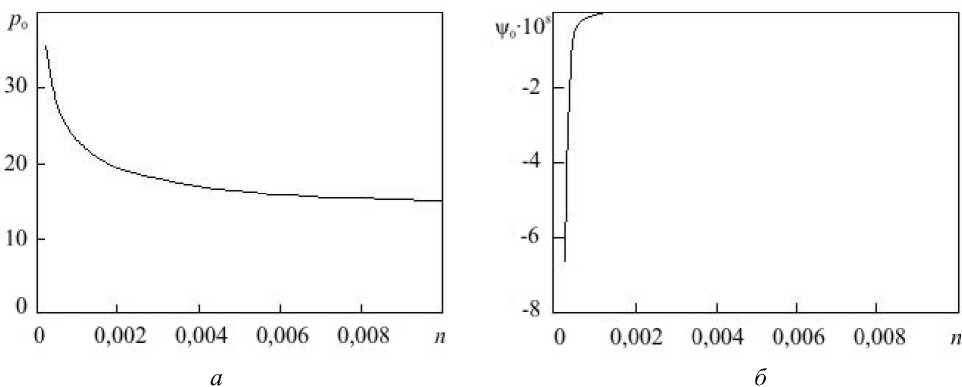
Рис. Результаты численного решения: положение фронта продольной ударной волны ( а ) и функция у ₀ ( n ) ( б) при значениях констант L = - 2, B = 2, D = - 1 -

• 4.    Поперечная плоская ударная волна в несжимаемой среде

Для выявления различия в процессе распространения поперечных и продольных ударных волн рассмотрим еще одну краевую задачу. Полупространство, ограниченное плоскостью x 1 = 0, занято нелинейно-упругой несжимаемой средой, поведение которой задается уравнениями (1), (2). Это позволяет остановиться только на свойствах сдвиговых волн. До момента t = 0 деформации отсутствуют. С момента t = 0 на границе действует сдвиговая нагрузка , такая, что

U 2I _; ;. = g ( t ) , g ( 0 ) = 0, g ' ( 0 ) > 0,                                                       (23)

приводящая к мгновенному образованию ударной волны. Поле перемещений в среде имеет вид u = u ₂ ( x 1 , t ) , u 1 = u ₃ = 0. Из уравнений (1)-(3) получим уравнение для скорости ударной волны

G 2 = C 2^/1 + 0 1 у + ^ , 0 1 = ( a + b + к + d )/ ц , C 2 = ЦР 0 ,

t .

I x j = I G 2 ( z ) dz

От системы уравнений (1), (2) перейдем к следующим двум уравнениям u 11 (1 + 301u) + ••• — u C2 +•••,

—P1 — O2 u 1 u 11 +... — 0, O2 — к + 2 (a + b + p), из которых наибольший интерес в настоящей работе имеет первое, позволяющее независимым образом определить поле перемещений. Интегрирование второго уравнения при найденных перемещениях не составляет труда. В дополнение к условию (23) для искомых функций u(x1, t), P(x1, t) запишем условия на поперечной ударной волне:

u l x , = J G 2 ( У ) dy ^’ t^] 1 x 1 = 1 G ₂ ( y ) dy

Прежде чем применим метод малого параметра, зададим безразмерные переменные в соответствии с формулами (7), с той разницей, что вместо функции u 1 ( x 1 , t ) теперь они будут включать u ₂ ( x 1 , t ) . Также в этих формулах заменим скорость C 1 на C ₂. Поскольку дальнейшее изложение аналогично приведенному выше, остановимся схематично только на получаемых результатах и их отличиях от результатов задачи распространения продольной волны.

Отметим, что первое уравнение (25), записанное в переменных (7), содержит только четные степени малого параметра а . Ввиду этого искомую функцию w ( 5 , m ) достаточно записать как ряд по четным степеням малого параметра. Этот ряд с удержанием переменных до четвертого порядка включительно имеет вид:

W0 (5, m) + а2W2 (5, m) + a4W4 (5, m) + . = f (^) + a2 °2L(f '(^))3 5 + +£402 {8(f,(^)4f"(^(52+^5—5)—30(f,(^))551+., ^=m—5, где f, как обычно, соответствует функции g (1) , записанной в новых переменных. Из этого решения следует, что область неравномерности по пространственной координате -2

возникает в случае 5 ~ в , то есть при иных расстояниях, чем в случае продольных волн. Определив новые независимые переменные формулами n = в ² s , p = 5 - m и записав в них уравнение (25), для внутреннего решения w ( n , p ) получим выражение:

( w, pp + 2в2 w, np + B4 w, nn ){1 + 361B2 ( w, p + B2 w, n )2 }+ - = w, pp , где w (n, p) также зададим как ряд по четным степеням в. Отсюда для нулевого приближения следует эволюционное уравнение вида v 0, n +Х1 v 2 v 0, p = 0, w0, p = v0, X1 = 1,561.                                                   (26)

Зависимость угла наклона его характеристик от квадрата функции v 0 ( n , p ) отличает процесс поперечного деформирования от продольного и обуславливает различия в образовании и движении ударных волн. Общее решение уравнения (26), имеющее вид v ₀ = F ( х 1 nv 0 - p ) , может использоваться при решении задачи в параметрическом виде:

W0 (У, n) = f(У)- 61 n (f'(У))3, p(У, n) = X1 n(f'(У)) - У, У ^ 0,

где w ₀ ( p ( у , n ) , n ) = W , ( у , n ) ; у — параметр.

При этом положению сдвиговой ударной волны на нулевом шаге соответствуют параметрические зависимости

= 3 ^f ( У ) -

p ^{0 ( У} ) 2 f '( y ) ^У ’ n ₍ y ) =     ^{f ( y} )

^{0 ( )} 6 ( f ' ( y ) ) 3 .

Ввиду ограничения объема статьи, здесь не приводим частные случаи решения (27), (28) при конкретных краевых условиях. По аналогии с решением для продольных волн может быть построено и последующее разложение решения для сдвиговой волны ( w ₂ ( n , p ) и так далее). Сравнение формул (14), (16) и (27), (28) показывает, что однотипные функциональные зависимости для перемещений на границе приводят к различным прифронтовым асимптотикам.

Дополнительно рассмотрим несколько краевых условий, позволяющих определить решение в явном виде. Вначале остановимся на условии, использовавшемся ранее для случая плоских продольных волн [14]

u\_xi = 0 = A11 + 0,5 A 2 1 \ (29)

которое приводило к частному решению уравнения (12), практически точно воспроизводящему условие (29) с учетом слабого затухания по пространственной координате. Для поперечной волны во внутреннем решении приходим к следующим формулам:

v 0 ( n, p ) =

w0 ( n, p ) =

- 1 + 71 + ^{4 ( B} 1 + ^B 2 p ) ^B 2 X 1 n

² B 2 X 1 n             ’         ₂

- 6 B 22 np X i + ( 1 + 4 ( B i + B 2 P ) B 2 X 1 n n^

12 B / n n

+ ¥0 (n),

где v ₀ ( n ) — пока не известная функция; B 1 и B ₂ — неопределенные константы; для p ²

функций v 0 и w 0 выполняются условия lim v 0 = B 1 + B ₂ p , lim w ₀ = B 1 p + B ₂ —. n ^ 0                    n ^ 0                   2

Формулы (30) показывают, что в отличие от краевых условий для продольных волн, квадратичная функция времени в краевом условии для поперечной волны воспроизводится только при n ∼ 0 ; для остальных значений получаем иную зависимость от времени. Сравнение внешнего и внутреннего разложений данного порядка

A 2 T1

показывает, что B, = - 1, B ₂ =---- , если в = AC .

A1

Для положения волнового фронта из формул (24) и уравнения эйконала на нулевом шаге решения имеем уравнение dP 0 (n)   61 2//

,    = V v0 ( n, P 0 ( n dn 2

Его сравнение с эволюционным уравнением (26) показывает, что отношение угла наклона ударной волны к углу наклона характеристик уравнения (26) равно 13, тогда как для продольных волн, на основе уравнений (12), (19), получаем значение 12. Интегрирование уравнения (31) с функцией v ₀ ( n , p ) , определенной формулой (30), позволяет задать положение ударной волны неявным образом.

(h -1) V2h +1 = -273B2X1 n, h = 71 + 4B2X1 n (-1 + B2p), откуда получим

p 0 (n ) = ^

2 r 3 cos---

cos² r + ¹ | + B. X, n

,     3 4 J ²¹

^B 22 X 1 n

,

cos r = - 2V3 B 2 X 1 n ,

n     3n

— < r < —

0, r = ^П, n = 0, 2

а затем найдем функцию у ₀ ( n ) в решении (30).

Приведенное решение показывает не только различия между процессами объемного и сдвигового деформирования при однотипных краевых условиях, но и преимущество параметрического решения перед явным. Построение последнего связано со значительными математическими трудностями уже при задании достаточно простых краевых условий.

Как еще один пример краевого условия, допускающего явное решение, рассмотрим условие  g (t ) = 0,8 At 54. Ему соответствует ситуация с нулевым значением интенсивности в t = 0. При этом квадрат интенсивности (v02) имеет вертикальную касательную в нулевой точке, что соответствует мгновенному возникновению ударной волны сдвига. Для нее решение на нулевом шаге во внутренней области будет таким:

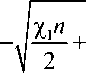
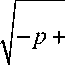
X i n

4 ⁽ IM + L p ./ - ⁿ 5 V 2 V 4

V

5 22

Р о ( n ) = ^X i n , 36

,     ( I---------1         2 2 V

2 X1 n    X1 n ,      „4. Xi n

+ Р +

3 Vv 2 \       4

Отметим, что положение ударной волны в этом случае задается особым решением Дарбу, к которому сводится уравнение (31).

• 5.    Заключение

Область применения эволюционных уравнений не ограничивается перечисленными примерами. Параметрический метод позволяет легко строить решения для краевых условий, заданных в виде экспоненциальной, логарифмической, тригонометрической зависимостей и других элементарных функций. На основе решений эволюционных уравнений внутри деформируемой области могут быть описаны как переходные волновые процессы, в которых ударные волны образуются не с начального момента воздействия, а с запаздыванием и, возможно, с отходом от нагружаемой поверхности, так и одномерные волновые процессы с волнами сильных разрывов, имеющими ненулевую кривизну [17].

Рассмотренные прифронтовые асимптотики использовались ранее в разработке схем численного счета, но в рамках одномерных задач ударного деформирования [5]. По мнению авторов статьи, полученные разложения применимы и к многомерным волновым процессам, так как, исходя из условий совместности Адамара [19] можно утверждать, что основные изменения в прифронтовой области ударной волны происходят по лучевому направлению. Поэтому эволюционные уравнения должны описывать решения в этой области, если только переменные в решаемой задаче выбраны специальным образом и соответствуют лучевой сетке. Кроме того, по крайней мере, на нулевом шаге, влияние координаты эйконала должно быть параметрическим. Безусловно, в таких задачах необходимо уточнение метода решения, связанное с присутствием в общем случае нескольких волновых фронтов.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-01-00001–а) и ДВО РАН (09-III-В-03-077).