Об оценке эффективности процесса фильтрации отработанных моторных масел через зернистые перегородки

Очистка ОММ от накопившихся механических примесей и продуктов деструкции масел – эффективное средство продления жизни моторных масел. Очищенное масло мы можем применять как базовое в гидравлических системах. Получение масел высокого качества очистки сопряжено с необходимостью использования ультрафильтрации. Однако ультрафильтрация имеет существенный недостаток, заключающийся в очень малом ресурсе работы такого фильтра (6–8 ч) в зависимости от загрязнения ОММ. Для повышения ресурса в работе [1; 2] предлагается использовать два фильтра. Фильтр первой ступени удаляет из масла частицы загрязнений размерами от 4 до 7 мкм, а также продукты деструкции масла (смолы, низко- и высокомолекулярные кислоты). На второй ступени очистки используют непосредственно ультрафильтр. В качестве фильтра первой ступени предлагается использовать насыпной фильтр, который позволяет удалять из ОММ как механические примеси, так и продукты разложения самого масла.

Фильтрующими могут выступать «зернистые материалы». Эти материалы имеют разное природное и производственное происхождение, разные экслуатационные характеристики. Среди них можно отметить активируемые угли, ионообменные смолы, а также неорганические сорбенты. Условием эффективной очистки ОММ от растворенных примесей (смол, низко- и высокомолекулярных кислот, других органических веществ, образующихся в процессе работы двигателя) является пористость материала. Одно из важных требований к такому материалу – минимальное взаимодействие с частицами масла. По данному критерию подходят активируемые угли.

Объекты и методы исследования

В процессе работы фильтра исходная структура засыпки изменяется, что приводит к изменению пористости, проницаемости (коэффициента фильтрации), физических характеристик засыпки и, как следствие, изменению фильтрационного режима фильтра.

Эти отклонения могут быть как полезными, так и нежелательными.

Выбранный материал для очистки ОММ играет большую роль для эффективности работы очистительной установки и должен отвечать определенным зависимостям. Эти зависимости напрямую влияют на конструктивную особенность фильтра и эффективность очистки.

Результаты и их обсуждение

На этапе фильтрации в зернистых перегородках фильтра откладываются загрязняющие элементы, что приводит к залипанию фильтра и, как следствие, к снижению его производительности и срока и службы. Чтобы избежать данную проблему, необходимо менять гидравлическое сопротивление. Теоретическое исследование динамики загрязнения фильтрующего зернистого слоя выполнено на основе системы уравнений Навье – Стокса [3; 4]. При этом предполагается, что процесс фильтрации является одномерным, т.е. идет в направлении одной оси:

Vestnik of Omsk SAU, 2024, no. 4 (56)

AGROENGINEERING

∂ u_ф     ∂ u_ф

+ u_ф

∂ t       ∂ х

-

1 ∂ р    ∂ ^{2 u} ф

+ ν     ,

ρ ∂ х    ∂ х ²

где u – скорость движения масла в зернистом слое, м/с;

• t – время, с;

• x – координата в направлении фильтрации, м;

• ρ – плотность масла, кг/м³;

• ν – кинематическая вязкость жидкости, м²/с;

• ∂ р / ∂ х – перепад давления в направлении оси х, Па/м;

• ∂ ²u / ∂ x² – вторая производная от скорости движения масла по направлению х, (м/с)/м².

Используя уравнение (1) и положения теории подобия и размерностей, мы получили следующие критерии, определяющие фильтрацию масла через зернистый слой:

R e =

E u

^иФ •^£.

; v ∆ p

=         ₂;

ρ⋅uф u⋅t

G =     ,

£ где R , E , G – безразмерные критерии подобия Рейнольдса, Эйлера и гомохронности соответственно;

£ - характерный размер, м.

В качестве характерного размера в формуле (2) принимали диаметр фильтра, равный 0,2 м.

Процесс изменения пропускной способности можно описать уравнением:

П = K ⋅ F ⋅ ^{∆ P} ,                                           (3)

n    µм⋅H где П – пропускная способность, м3/с;

• K – коэффициент пропорциональности, м²;

• F – площадь фильтрующего материала, м²;

• Δ Р – перепад давления, Па;

• µ – динамическая вязкость масла, Па·с;

• Н – высота фильтрующего материала, м.

Для оценки загрязненности фильтра необходимо из критериального уравнения, включающего критерии (2), экспериментально определить критерий Эйлера в виде функциональной зависимости:

E u = f(Re,G) ,                                          (4)

• а затем из формулы критерия Эйлера определить ∆Р:

Δ P = E u ⋅ ρ ⋅ u ф ² = ρ ⋅ u ф ² ⋅ f ( R e , G ) .

Обычно в гидродинамике и теплотехнике при поиске функциональной зависимости (4) неизвестную функцию представляют в виде:

Vestnik of Omsk SAU, 2024, no. 4 (56)                                                              AGROENGINEERING

E u =aR e ^δ ⋅G^β                                               (6)

, где а, δ, β – экспериментальные коэффициенты.

С учетом формулы (6) зависимость (5) для определения потери давления примет вид:

Δ P = aR e ^δ ⋅ G ^β ⋅ ρ ⋅ u ф ²                            (7)

Анализ зависимости (7) показывает: перепад давления зависит от величин, входящих в критерий Рейнольдса (линейно от скорости фильтрации и диаметра частиц, обратно пропорционально вязкости ОММ); и величин, характеризующих критерий гомохронности (линейно u ^β и t ^β , обратно пропорционально размеру зерен засыпки).

Для определения коэффициентов уравнения (6) и проверки адекватности модели была проведена серия экспериментов на экспериментальной установке, представленной на рис. 1. Экспериментальные исследования проводили с фильтром 1, имеющим однородную загрузку полиэтилена в виде гранул. Диаметр фильтра d ф = 0,3 м, высота засыпки Н = 1,5 м. Исходная пористость материала фильтра – 0,8. Размеры частиц полиэтилена – 3,4–4 мкм. Исходное ОММ для очистки было получено из картеров тракторов МТЗ-80/82, К-701 в различных хозяйствах Омской области.

Эксперименты проводили в следующей последовательности.

Собранное в хозяйствах ОММ подвергалось предварительной очистке для удаления крупных механических примесей и воды путем отстоя в отстойнике при температуре 100–105оС в течение 24 ч. После слива отстоя масло подвергали центрифугированию на установке, собранной на базе центрифуги трактора МТЗ-80 [5–7].

Проводили анализ физико-химических и эксплуатационных параметров масла после центрифугирования. Результаты анализа представлены в таблице.

Результаты анализа ОММ, подвергшегося очистке путем отстоя и центрифугирования

№ опыта	Ν при 100оС, мм2/с	Н 2 О, %	рН, мгКОН/г	Содержание механических примесей, %	ρ, кг/м3
	11,63	0,014	6,2	0,0134	910
1	12,26	0,011	6,3	0,0128	907
	11,33	0,004	6,5	0,0131	910
среднее	11,74	0,009	6,33	0,0131	909
	11,87	0,076	6,1	0,0124	903
2	11,59	0,064	6,7	0,0114	907
	11,42	0,032	7,5	0,0122	908
среднее	11,62	0,057	6,77	0,0120	906
	15,21	0,006	6,8	0,0097	904
3	12,42	0,017	7,1	0,0099	906
	12,34	0,011	7,6	0,0105	902
среднее	13,32	0,011	7,17	0,0100	904

Перепад давления на фильтрах контролировали через 5 ч работы фильтра. Предварительно очищенное путем отстоя и центрифугирования отработанное моторное масло содержит в себе механические примеси в количестве от 0,01 до 0,0131%. Давление выхода измерялось манометром 8 при открытом вентиле 9 (рис. 1). Следовательно, перепад давлений (МПа) на фильтре определяли как разность давлений на входе и выходе фильтра:

Vestnik of Omsk SAU, 2024, no. 4 (56)

AGROENGINEERING

Др = Рвх - РвыX, ф     вх     вых где рвх – давление на входе в фильтр, МПа; рвых – давление на выходе из фильтра, МПа.

Давление на выходе из фильтра определяли по формуле:

Р вых = Р о ^{+Д Р} ,                                           ⁽⁹⁾

где р 0 – давление окружающей среды, Па;

∆Р – потери давления в фильтре.

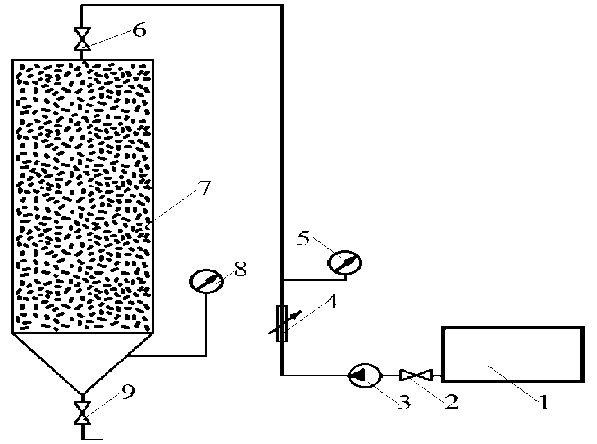
Рис. 1. Принципиальная схема установки: 1 – емкость масла; 2 – вентиль; 3 – насос; 4 – регулятор давления; 5 – манометр; 6 – вентиль; 7 – насыпной фильтр; 8 – манометр; 9 – вентиль очищенного масла

Обработка результатов экспериментов позволила получить уравнение (10) в следующем виде:

Д Р = 1,8052 ■ R ^,³³⁰² . G ¹,⁰⁰⁵⁸ .р. и_ф ² .                                     (10)

Результаты расчетов зависимости критерия Эйлера от критериев Рейнольдса и гомохронности представлены на рис. 2.

Анализируя рис. 2 и его показатели, мы видим, что критерий Эйлера возрастает. Это происходит с увеличением критерием Рейнольдса и [8–10].

С увеличением критерия Рейнольдса от 0,5 и до 10 при критерии гомохронности, равном 0,5, критерий Эйлера изменился от 0,9 до 19. При увеличении критерия гомохронности (времени очистки ОММ) и постоянном критерии Рейнольдса критерий Эйлера возрастает более интенсивно. Если при критерии Рейнольдса равном 5 и критерии гомохронности равном 0,5 критерий Эйлера составлял 7,65, то при критерии гомохронности, равном 10, критерий Эйлера возрастает до 155,63. Критерий Эйлера прямо пропорционально зависит от перепада давления (2). Нами были проведены расчеты потерь давления пропускной способности фильтрации в зависимости от времени работы фильтра.

Vestnik of Omsk SAU, 2024, no. 4 (56)

AGROENGINEERING

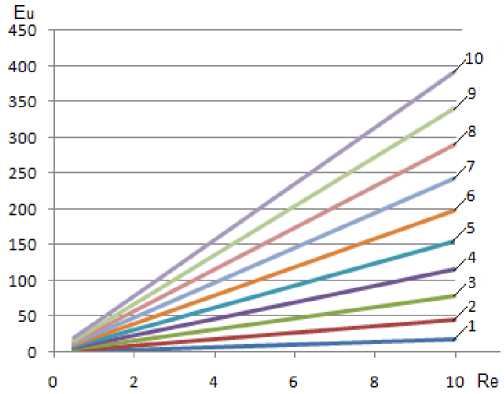
Рис. 2 . Зависимость критерия Эйлера от критерия Рейнольдса (Re) и критерия гомохронности G: 1 – G = 1; 2 – G = 2; 3 – G = 3; 4 – G = 4; 5 – G = 5; 6 – G = 6; 7 – G =7; 8 – G = 8; 9 – G = 9; 10 – G = 10

Результаты расчетов потерь давления по формуле (10) в зависимости от скорости и времени фильтрации представлены на рис. 3.

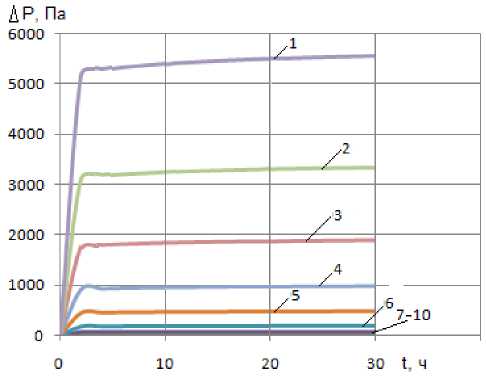
Рис. 3. График функций 1 – ∆Р=f(t,u ф ): 1 – u ф = 0,001 м/с; 2 – u ф = 0,0009 м/с; 3 – u ф = 0,0008 м/с; 4 – u ф = 0,0007 м/с; 5 – u ф = 0,0006 м/с; 6 – u ф = 0,0005 м/с; 7 – u ф = 0,0004 м/с; 8 – u ф = 0,0003 м/с;

9 – u ф = 0,0002 м/с; 10 – u ф = 0,0001 м/с

Потери давления, в зависимости от критерия гомохронности, увеличиваются практически по линейному закону. Показатель степени β = 1,0058. Большее влияние на нелинейность зависимости ∆Р = f(t) оказывает критерий Рейнольдса (показатель степени δ = 1,3302).

Анализ представленных на рис. 3 графиков показывает, что время и скорость фильтрации оказывают существенное влияние на потери давления в насыпном фильтре. При скоростях фильтрации от 0,0001 до 0,0004 м/с (кривые 7–10) в течение 30 ч скорость фильтрации оказывает незначительное влияние на потери давления и не превышает 65 Па, однако с увеличением скорости фильтрации потери давления существенно возрастают. При скорости фильтрации u ф = 0,0005м/с они составляют 200 Па, а при u ф = 0,001м/с они достигают 5500 Па. Влияние времени фильтрации существенно в начальный период

Vestnik of Omsk SAU, 2024, no. 4 (56)

AGROENGINEERING

фильтрации – 1...2 часа. В это время потери давления при данной скорости фильтрации достигают практически максимального значения (примерно 90–95%) от максимальной величины потерь давления. При дальнейшем процессе фильтрации потери давления увеличиваются незначительно и составляют 5...10% общих потерь давления [11].

При расчете пропускной способности насыпного фильтра по формуле (3) для согласования результатов расчета и экспериментальных данных коэффициент пропорциональности Kn принимали равным Kn = 1,31·10-10 .

На рис. 4 приведены расчитанные по формуле (3) данные по изменению пропускной способности насыпного фильтра в зависимости от его высоты Н и потери давления ΔР.

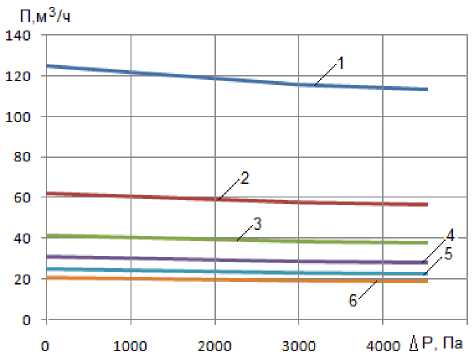
Рис. 4. Зависимость пропускной способности насыпного фильтра от потери давления Δр и высоты засыпки в фильтре Н: 1 – Н = 0,5 м; 2 – Н = 1,0 м; 3 – Н = 1,5 м; 4 – Н = 2,0 м; 5 – Н = 2,5 м; 6 – Н = 3,0 м

Анализ графика П =f(t,Н) показывает, что пропускная способность фильтра падает как при увеличении потерь давления, так и при увеличении высоты фильтра. При высоте фильтра 3 м и пропускная способность изменяется незначительно – от 20,82 до 18,86 м3/ч давлении 0 Па. С уменьшением высоты засыпки пропускная способность фильтра увеличивается и при высоте фильтра Н = 0,5 м составляет более 120 м3/ч, а при потере давления 4500 Па – снижается до величины 113 м3/ч.

Заключение

Полученные зависимости позволяют сделать точные инженерные расчеты: пропускной способности используемого фильтра и потерь давления.

Исходя из анализа критериев Рейнольдса и гомохронности на критерий Эйлера их увеличения, мы делаем вывод, что вследствие загрязнения идет рост потери давления.

Увеличение потерь давления и высоты засыпки приводит к снижению пропускной способности фильтра. Окончательное суждение об оптимальных размерах фильтра и режимах его работы можно принять только после проведения исследований по тонкости очистки масла.