Об оценке погрешности нелинейного метода проекционной регуляризации при условии кусочной гладкости решения
Бесплатный доступ
Нелинейным методом проекционной регуляризации, приведенном в [1], получено приближенное решение обратной задачи Коши для уравнения теплопроводности. Получены оценки погрешности приближенного решения в классе кусочно-гладких функций. Эти оценки гораздо лучше, чем известные ранее оценки оптимальных и оптимальных по порядку методов решения данной задачи.
Обратная задача, регуляризация, оценка погрешности, некорректная задача, преобразование фурье
Короткий адрес: https://sciup.org/147158682
IDR: 147158682 | УДК: 517.948.00
About error estimate of nonlinear projection regularization method under the condition of priece-wise smoothness of solution
An approximate solution for the inverse Cauchy problem for the heat conduction equation is obtained by means of nonlinear projection regularization method. Error estimates for the approximate solution are obtained in the class of piecewise smooth functions. These estimates are better then the known estimates for the optimal and the order- optimal methods of solving the problem.
Текст научной статьи Об оценке погрешности нелинейного метода проекционной регуляризации при условии кусочной гладкости решения
Рассмот^им у^авнение д u (x, t) _ д 2 u (x, t)
-x<
x
V t e ( 0, T ] u ( x , t ) ,
д t " дx2 ’ где u(x,t) e C{(-x,x)x[0,T]} Q C2,1 {(-x,~)x(0,T]}, u"x. (x,t)e L1 (-x,x)Ql2 (-x,x) и существует функция x(x)e L1 (-x,x) такая, что
I u ( x , t )| +
д u ( x , t ) д t
< x ( x ) ; x e ( -x , x ) .
Пусть нам дано распределение температуры f (x)e L1 (-x, x) Q L2 (-x, x) в момент времени T f (x ) = u (x, T); -x< x a начальное ^асп^еделение u o( x) = u (x ,0) (3) т^ебуется оп^еделить. Предположим, что при f (x) = f0(x) существует u0(x) такое, что производная u0(x) является четной, кусочно-непрерывной функцией и u0(x), u0(x)e L2(-x,x)QL1 (-x,x), а также решение задачи (1), (3) при нем удовлетворяет условию u(x,T) = f0(x), но точное значение f0(x) нам не известно, а вместо него даны некоторое приближение f5(x) e L1 (-x, x) Q L2 (-x,x) и 5 > 0 такие, что I f5 ( x)- f0 ( x)||L2 < 5. Требуется, используя исходные данные (f5,5) задачи (1), (2), (4), определить приближенное решение u5(x)e L2(-x,x) и оценить величину ||u5(x)-u0(x)||L2. Используя для ^ешения задачи (1), (2), (4) п^еоб^азование Фу^ье F , получим й ‘(Я, t ) = -X2 й (Я, t); le(-x, x), t e( 0, T ] u( Я, T ) = f (Я); Яe(-x, x),(6) где й(Х, t) = F [u (x, t)], а f (Я) = F [f (x)]. Решая задачу (5), (6), сведем ее к опе^ато^ному у^авнению Ай(И) = e—И Tu(И) = f(И); й(И), f(И)е L2(—^, Из условий, кото^ым удовлетво^яет функция u0(x) , будет следовать существование числа a > 0 такого, что для любого достаточно малого числа е > 0 ^ J[1+И ) ] ^ (И2dx< е, —^ а из (4) и тео^емы Планше^еля [3, с. 411], что I A»0 (A — f (И)|< 3, где /уШ = F[и0 (x)],а f(И) = F[f5(x)]. П^именяя к ^ешению задачи (7)–(9) метод п^оекционной ^егуля^изации [1], введем ^егуля-ризующее семейство операторов {Pa : a > 0}, определяемых формулой Pa f ( И) = еИ Tf (И); И < a 0; Al > a . Таким образом, приближенное решение 3 (И) в уравнении (7) определим формулой «3 ( A) = Pa f3 ( A), а для выбора параметра регуляризации a = a( f3,3) в формуле (11) используем уравнение JАйР3 (A) — f3 (Л)|^ -1632. Из (11) и (12) определим приближенное решение г/3 (И) уравнения (7) формулой ~a(f3,3) / 1 \ и3 (И) = и3 (И)- Из тео^емы, доказанной в [1], и фо^мул (7), (8), (9) следует оценка II83 (И)—«0 (И)||< 7 ^ [a(3)], в которой функция Ое (с), следуя (7) и (8), определяется параметрически с = e Ge (^)= 1 + Ri' ’ Ие (—”,~) 1. 2, a a(3) - уравнением aGGe (a )a = 3. Так как оценка (13) выполняется при любом ее (0,1], то выберем значение е(3), минимизирующее эту оценку. Ввиду непрерывности функции 7^Ge(a(3, е)) пое на полуотрезке (0,1] и стремление ее к бесконечности при е ^0 следует существование е(3)е(0,1] такого, что 7\^°е(3) (a3 е(3))) = Д711Се(a(3, е))" \| с\и ) ее(0,1] у е Тогда из (13)-(16) для £13 (И) будет справедлива оценка Камалтдинова Т.С. Об оценке погрешности нелинейного метода проекционной регуляризации при условии кусочной гладкости решения Iй8(Л)-ио(Л)||<7 Г8G£(,)[а(8,е(8))]. (17) Применяя к й8 (Л) обратное преобразование Фурье F 1 и беря действительную часть, полу чим приближенное решение и5 (x) = Re| F 1 (й5 (Л)) | обратной задачи (1), (2), (4). Для этого ре- шения, ввиду тео^емы Планше^еля [3, c. 411], будет сп^аведлива оценка (17). Для с^авнения (17) с известными, оценим п^авую часть соотношения (17) в элемента^ных функциях. Из (14) следует, что при достаточно малых значениях с справедливо соотношение а из (18) и того, что - (1- е) —(1-е) 1 Ge(с)<T4 ln 4 -, с lim '"""-----= 1, ■ "0 T 4’ ln-4 (1-е’1 с следует, что при достаточно малых значениях с 3(1-е) 9 T4 с2< сGе(с). Тепе^ь ^ассмот^им у^авнение T 4(1-е ’а2= 8. Решение а(8,е’ уравнения (20) определяется формулой а (8, е ) = T" 8(1-е ’ кд ] 2 \ a Из (15), (19) и (20) следует, что а(8, е )< а (8, е). Таким об^азом, из (13), (18) и (22) следует, что и и а 3(1-е’ -3(1-е’ IIu8(x)-uо(x)||<7^е4 ln4 Из (21) и (23) окончательно получим II и8 (x)-u о (x )|<7^е (2T) 4 (1"е ’ ln4(1 е ’ а (8, е) 3(1-е ’ T4 а е88 В оценке (24) значение е = е(8) определим формулой е (8 ) = 2a lnln1 Из (24) и (25) следует, что || u8 ( x )-и 0 (x)||< |V2 ( 2T )4^lnln 8 In 4(1 e(8’’ Vlnln 8 Если lnln — > V2, то при 8e (0,80] из (26) следует, что 8о 3 - 3(1-s(s )W us(x)-u0(x) 2 vs V s Так как 3a —(1-£(s)) < 1 A — < 1 A 2lnln- < 1 A ln 4 — = In 4 — • In s — , V s J V s J V s J а 3a ln ln 2lnln1 s 3a 2lnln s lnln- = s 3a 2, то из (27) следует, что 7 ^3a 3 - - 3 \ 3 a 3 / “ 3 s J s 3 3 ||us(x)-u0(x)||<2^2e2(2T)4 Jlnln^In 4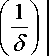
Список литературы Об оценке погрешности нелинейного метода проекционной регуляризации при условии кусочной гладкости решения
- Танана, В.П. Об оптимальном по порядку методе решения условно-корректных задач/В.П. Танана, Н.М. Япарова//Сиб. журн. вычисл. матем. -2006. -Т. 9, №. 4. -С. 353-368.
- Колесникова, Н.Ю. О проблеме потери точности при преобразовании информации/Н.Ю. Колесникова, Т.Н. Рудакова, А.В. Танана//Вестник ЮУрГУ. Серия «Компьютерные технологии, управление, радиоэлектроника». -2010. -Вып. 11. -№ 2(178). -С. 56-62.
- Колмогоров, А.Н., Фомин СВ. Элементы теории функций и функционального анализа/М.: Наука, 1972.-496 с.
- Tanana V.P., Yaparova N.M. Siberian Journal of Numerical Mathematics. 2006. Vol.9, no. 4. pp. 353-368. (in Russ.).
- Kolesnikova N.Yu., Rudakova T.N., Tanana A.V. Vestnik YuUrGU. Seriia «Komp'iuternye tekhnologii, upravlenie, radioelektronika». 2010. Vol. 11, no. 2(178). pp. 56-62. (in Russ.).
- Kolmogorov A.N., Fomin S.V. Elementy teorii funktsii i funktsional'nogo analiza (Elements of Function Theory and Functional Analysis). Moscow, Nauka, 1972. 496 p. (in Russ.).
