Об оценке погрешности приближенного решения одной обратной задачи физики твердого тела
Автор: Танана Виталий Павлович, Ерыгина Анна Александровна
Рубрика: Математика
Статья в выпуске: 2 т.5, 2013 года.
Бесплатный доступ
Изучена задача определения фононного спектра кристалла по его теплоемкости. Получена оценка точности метода регуляризации А.Н. Тихонова с параметром регуляризации, выбранным из принципа невязки.
Регуляризация, модуль непрерывности, оценка погрешности, некорректная задача
Короткий адрес: https://sciup.org/147158789
IDR: 147158789 | УДК: 517.948
Текст научной статьи Об оценке погрешности приближенного решения одной обратной задачи физики твердого тела
Эта задача в известной статье Лифшица [4] была сведена к интегральному уравнению первого рода, что доказывает ее некорректность.
Ввиду важности для физиков знание оценки погрешности приближенного решения данной задачи следует актуальность приведенных в статье исследований.
1. Постановка задачи. Связь энергетического спектра бозе-системы с ее теплоемкостью, зависящей от температуры, описывается интегральным уравнением первого рода
J „< е 7 е . E C( 9 )
0 ≤ θ < ∞ ,
Sn ( ε ) = S n ( ε ) = ;
0 V 9) 9 е 9
x 2 где S ( x ) = ,
2sh 2 ( x 2 )
C(θ) – теплоемкость системы, θ= kT , T– абсолютная температура, а k – константа, определяемая системой, n(ε) – спектральная плотность [4].
Обозначим через H действительное пространство измеримых на [0, ∞ ) функций f (x) с нормой, определяемой формулой
Ilf (x )iH-Jif (xf dx■(2)
0 x
Заметим, что интеграл в формуле (2) понимается в смысле Лебега.
С(9) С. (9) -. .
Предположим, что при =0 ∈H существует точное решение n0(ε)∈H уравнения (1), которое единственно и удовлетворяет соотношению n0(ε) ∈ Gr,где
Gr - Jn(е): n(е) е H, J n (E) dE + J [n'(е)]2 EdE < r2 [, l о E 0J
. C n ( 9 )
где n ′ ( ε ) – производная от функции n ( ε ), но вместо точного значения правой части 0
Cs (9) -„ „ нения (1) известны некоторое приближение δ ∈ H и уровень погрешности δ> 0 такие, что θ
C δ ( θ ) θ
C 0 ( θ ) θ
H
Требуется определить приближенное решение n δ ( ε ) ∈ H уравнения (1) и оценить уклонение n δ ( ε ) - n 0( ε ) H от точного решения n 0( ε )в метрике пространства H .
C ( О )
Если предположить, что , n ( е ) е H , то уравнение (1) становится некорректной задачей.
θ
2. Метод регуляризации А.Н. Тихонова. Метод регуляризации А.Н. Тихонова [1] для приближенного решения уравнения (1) заключается в сведении его к вариационной задаче
2 1
∞
∞
inf И f s I E I E n ( E ) d ^ — C ^ ^ ^ ) j - j V О) О E
ε
-
θ
∞
dθ+α θ
∞
j[ n '(е )] 2 E d E + a J n 2( е ) —: n ( е ) е H 1 [0, га ) [ , 0 0 е
где H 1 [0,да) - гильбертово пространство, определяемое нормой
∞
IH 'ига, I
n 2( е )
ε
Известно из [5], что для любой функции
∞
d E + j [ n '( е )]2 E d E , а a > 0.
C8 ( О ) „
—--е H существует единственное решение ва-
θ
риационной задачи (4).
Для определения значения параметра регуляризации a в задаче (4), используется принцип невязки [2, 3], который сводится к решению уравнения
∞
∞
ε
ε
Г с с| E I E a d EE J J S kk n s ( E )— — о . Г> v О ) О E
d E С 5 ( О )
θ
d O „2
=δ θ
относительно a .
∞
C 5 ( О ) θ
dO „
■ о > 5 , уравнение (5) имеет единст-
Известно [3], что при выполнении условия j
0 - венное решение a(С5,5).
Приближенное решение n5 (е) уравнения (1) определим формулой n5 (E) = n5(C5,5 )(E ), соответствующий метод регуляризации определим семейством операторов {R5 : 0 < 5 < 50} непрерывно отображающей H в H и определяемый формулой
R δ
C 5 ( О ) θ
n § ( E ),
C 5 ( О ) θ
H
0,
C 5 ( О ) θ
< 5 .
H
3. Оценка погрешности метода { R g : 0 < 5 < 5 0} на классе решений G r . Оценку погрешности метода { R 5 :0 < 5 < 5 0} определим с помощью семейства функционалов { А 5 ( R 5 ): 0 < 5 < 5 0} определяемых формулой [6]
А 5 ( R 5 ) = sup ^ R 5
С"^ ) — n 0 ( E ) О )
: n о( е ) е G r , С 5 О ) е H , Sn о( е ) H θ
^^^^^^™
C 5 ( О ) θ
Обозначим через w ( 5 , r ) модуль непрерывности в нуле оператора S " 1 на множестве S [ G r] w ( 5 , r ) = sup{11 n( E ) | H : n ( e ) е Gr ,|| Sn ( e ) 11 < 5 }.
Для величины А 5 ( R 6 ) в [7] получена оценка
А8 ( R 8 ) < 2 w ( 5 , r );0 < 5 < 5 о ,
где w(5,r) определен формулой (7), а А 5 ( R § ) формулой (6).
4. Оценка модуля непрерывности w ( д,r ), определенного формулой (7). Сделаем замену переменных
е=€? и 6 = eT; —га < t < га, —га < т < га после которой оператор S сведется к оператору A типа свертки
Математика
∞
Au ( t ) = J K ( t — t ) u ( t ) dt ; 7< t <7 , —7 < т <7 , (10)
-∞ u (t) = n (e1),
-
- — 3 x
k ( x ) =------ x , 2sh2 —
I 2 J кроме того u(t), Au(t)e L2(-«,«).
Заметим, что после замены (9) класс корректности G r, определяемый формулой (3) перейдет в множество M r
Mr = {u (t): u (t) e W21(—7, 7), J u 2( t) dt + J |u'(t )|2 dt < r2}.(11)
-∞-∞
Теперь определим модуль непрерывности в нуле оператора A -1 на множестве N r= AM r формулой
w(3,r) = sup{||u(t)||L2: u(t)e Mr,\\Au(t) ||k< 3}.(12)
Лемма 1. Пусть w ( 3 , r ) определен формулой (7), а w ( 3 , r ) формулой (12). Тогда справедливо равенство w ( 3 , r ) = w ( 3 , r ).
-
5. Оценка модуля непрерывности w ( 3 , r ) , определенного формулой (12)
Полагая, что u ( t ) e L 1 ( —7 , 7 ) n L 2( —^ , 7 ), определим преобразование Фурье F
F [ u ( t )] =
72 Л
∞
J u ( t ) eip p dt .
-∞
Из теоремы Планшереля следует изометричность преобразования F в пространстве L 2 (-»,«). Чтобы отличать комплексное пространство от действительного, будем обозначать его L 2 ( —7 , 7 ). Таким образом, оператор F , определяемый формулой (13) будет изометрично в метрике L 2( —^ , 7 ) отображать множество L 1 ( —7 , 7 ) n L 2( —^ , 7 ) в пространство L 2( —^ , 7 ).
Ввиду того, что пространство L1(—7, 7) плотно в L2(—^, 7), расширим оператор F на все пространство L2 (—7, 7). Это расширение обозначим через F .
Теперь оператор F будет изометрично отображать пространство L 2( —^ , 7 ) в L 2( —^ , 7 ). В дальнейшем образ оператора F обозначим через Y и заметим, что Y будет являться подпространством L 2( —^ , 7 ).
После преобразования F оператор A сведется к следующему
Au(p ) = K ( p ) u(p ); u(p ) e Y , а v Au(p ) e L 2 ( —^ , ~ ), (14)
где й(p ) = F [ u ( t )], а ввиду того, что K ( x ) e L 1 ( —^ , ~ )
2 П
∞
K C( p ) =
J K ( x ) e ixp dx .
-∞
Из вида K(x) будет следовать, что
A 1 7 e—(2—ip)xe—x 7 e—(2—ip)xe—e d (e—x).
K C( p ) = J e-----— dx . = —. - J e-----—
2 П — —7 ch( e x ) — 1 V n —7 ( e-e x — 1) 2
Сделав в последнем выражении замену z = e"- , получим
......Л J
-∞
z — (2 — ip ) ez ( e z — 1) 2
dz =
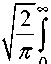
z — (2 — ip ) ez ( e z — 1) 2
dz .
Используя свойства гамма и дзета-функций [8]
~ s - - 1
Г ( s ) Z ( s ) = J Zz , 0. e - 1
получим, что
Kp) = p(2 - ip)Г(2 - ip)Z(2 - ip) = £Г(3 - ip)Z(2 - ip), ππ где Г(z) - гамма функция Эйлера, а Z(z) — дзета-функция Римана.
Для оценки снизу поведения функции |к(p)| при p^x приведем некоторые известные свой ства гамма-функции, сформулированные в [8, стр. 16 и 19]:
Г(7+1) = 2Г(Х),(15)
_ Г( z) = Г( z),(16)
где z сопряжено z , а Г ( z ) сопряжено Г(/) и
Г(z)Г(1 - z) = -П.(17)
sin n z
Таким образом, из (15) следует, что
I Г(3 - ip )| = TiTp2 Т4+Т2 |Г(1 - ip )|,(18)
а из (16) и (17), что
| Г(1 - ip)| = np.(19)
sh п p
Из (18) и (19) для любого p > 2 справедлива оценка
|Г(3 - ip)| > V2ne"2p .(20)
Теперь перейдем к оценке снизу модуля дзета-функции Римана Z (2 - ip ) .
Так как ∞
Z( s) = I -,(21)
n=1 n то из (21) следует, что
^ ip ln n
Z(2 - ip) = I -2-.(22)
n = 1 n
Учитывая, что | e ip ln k | = 1, из соотношения (22) получим
Z(2 - ip) > 1 -I > 1.(23)
n = 2 n 3
Таким образом, из (20) и (23) следует, что при p > 2 справедлива оценка снизу
- π P
|Kp)| > je 2 .(24)
Теперь рассмотрим расширение Д оператора 4 , определенного формулой (14) на все пространство L 2( -м , м )
Л u(p) = K(p)u(p); u(p),Д u(p)e L2( ^.~).
Рассмотрим множество M r c L 2 ( -^ , ~ ) и определяемое формулой
Л/ r = {ut( p): u( p), pu( p) e L2(—,-), J (1 + p 2) ^( p )|2 Zp < r2}.(26)
-∞
Тогда из (11) и (26) следует, что
F [ Mr ] c Mf r.(27)
Теперь рассмотрим модули непрерывности, в нуле определяемые формулами
Математика
|
Tw( 5 , r ) = sup{| u ( p ) L : zz( p ) e F [ M r ]Jplzz( p ) < 5 }, 2 L 2 |
(28) |
|
4w ! ( 5 , r ) = sup !) u ( p ) L : u(p ) e M r J . 4 1 u(p ) < 5 } . 2 L 2 |
(29) |
|
Из унитарности преобразования F и формул (10), (12), (14) и (28) следует, что |
|
|
w( 5 , r ) = w ( 5 , r ), |
(30) |
|
а из (14), (25), (27)-(29), что |
|
|
iw’1( 5 , r ) > vw( 5 , r ). |
(31) |
Таким образом, из (30) и (31) следует, что w (5, r) < w1(5, r).
Для удобства изложения оператор 4 , определенный формулой (25) заменим обратным
I f1, который обозначим через T 1
T1 Л p) = 4- f( p); f( p) e R (41), T1 Д p) e L2(—, ~),(32)
где R (4) - множество значений оператора 4 1 .
Множество Mlr , определенное формулой (27) зададим с помощью оператора B
Bu(p) = 71 + p2м(p); u(p),Bu(p) e L2(-~,~),(33)
Mr = B 1 Sr,(34)
где S r = {t?( p ): u(p ) e L . ( -~ ),||tz( p )|| L < r }.
В пространстве L 2( -^ , ~ ) введем множество T V r определяемое формулой
Vr = VC Mr).(35)
Тогда из (26), (29), (32)-(34), (35) следует, что w1(5,г) = sup{|Tf(p)||:f(p)e TVЦf(p)||_ < 5}.
Перейдем к оценке модуля непрерывности w ( 5 , г ).
Для этого рассмотрим оператора T, действующий из L 2( -^ , ^ ) в L 2( -^ , ^ ) и определяемый формулой
Tf p ) = g ( p ) f p ), (36)
Где
g(p ) e С(-да,да), g (- p ) = g(p ), g (0) > 0, (37)
lim g ( p ) = ~ и g(p ) возрастает на [0, да).
p ^^
Обозначим через w2(5,г ) модуль непрерывности в нуле оператора T на множестве T V r = T - 1 ( Mlr ), а Mlr определено формулой (34) и рассмотрим уравнение
^= = g ( p) 5 . (38)
71+ p
Если g (0) § < г , то уравнение (38) имеет единственный положительный корень p ( 5 , г ).
Из леммы доказанной в [6] следует, что
* 2 ( 5 , г ) = , _r . (39)
71 + p 2( 5 , r )
Предположим, что оператор T 1 определен формулами (25) и (32), а T формулой (36).
Тогда справедлива лемма.
Лемма 2. Если g(p ) удовлетворяет (37) и существует p 0 > 0 такое, что для любого p > p 0 справедливо соотношение
Kˆ(p)-1 ≤g(p), то при условии, что g(p0)δ< r справедлива оценка
-
1 + p 0 2
w ˆ 1( δ , r ) ≤ w ˆ 2( δ , r ).
Теперь используем лемму 2 для оценки точности метода{ R δ :0 < δ ≤ δ 0}.
Из (24) следует, что при p ≥ 2
π
- 1 p
K ˆ( p ) ≤ 3 2 e 2 .
Таким образом, из (8), (30), (31), (39), (40) и леммы 2 следует, что при
2 re - π
δ 0 = 35
для метода { R δ :0 < δ ≤ δ 0}справедлива оценка
Δ δ ( R δ ) ≤
2 r
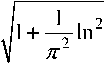

Список литературы Об оценке погрешности приближенного решения одной обратной задачи физики твердого тела
- Тихонов, А.Н. О решении некорректно поставленных задач и методе регуляризации/A.Н. Тихонов. -Докл. АН СССР. -1963. -Т. 151, № 3. -С. 501-504.
- Иванов, В.К. О приближенном решении операторных уравнений первого рода/В.К. Иванов//Журн. вычислит. мат. и мат. физ. -1966. -Т. 6, № 6. -С. 1089-1094.
- Морозов, В.А. О регуляризации некорректно поставленных задач и выборе параметра регуляризации/В.А. Морозов//Журн. вычислит. мат. и мат. физ. -1966. -Т. 6, № 1. -С. 170-175.
- Лифшиц, И.М. Об определении энергетического спектра бозе-системы по ее теплоемкости/И.М. Лифшиц//Журн. экспериментальной и теоретической физики. -1954. -Т. 26, вып. 5. -С.551-556.
- Васин, В.В. Приближенное решение операторного уравнения первого рода/В.В. Васин, B.П. Танана//Мат. зап. Уральск. ун-та. -1968. -Т. 6. -Тетр. 2. -С. 27-37.
- Танана, В.П. Об оптимальных по порядку методах решения условно-корректных задач/В.П. Танана, Н.М. Япарова//Сиб. журн. вычисл. матем. -2006. -Т. 9, № 4. -С. 353-368.
- Танана, В.П. Об оптимальности методов решения нелинейных неустойчивых задач/В.П. Танана. -Докл. АН СССР. -1975. -Т. 220, № 5. -С. 1035-1037.
- Уиттекер, Э.Т. Курс современного анализа/Э.Т. Уиттекер, Дж.Н. Ватсон. -М.: Наука, 1978.-Ч. 2. -С. 468.


