Об оценке величины оттока жидкости из глаза с помощью модифицированного метода тонографии

Первичная открытоугольная глаукома – одна из основных причин потери зрения и инвалидности по зрению во всем мире [1, 9]. Ведущими факторами, способствующими развитию этого заболевания, считают повышение внутриглазного давления и патологию дренажной системы глаза, что приводит к нарушению гидродинамики внутриглазной жидкости [5, 6]. В настоящее время единственным клиническим способом оценки гидродинамических показателей глаза является тонография, однако результаты этого исследования, поступающие врачу, далеко не всегда отражают реальное функциональное

Любимов Григорий Александрович, д.ф.-м.н., профессор, г.н.с. института механики МГУ, Москва Моисеева Ирина Никитична, к.ф.-м.н., с.н.с института механики МГУ, Москва

Штейн Александр Александрович, к.ф.-м.н., в.н.с института механики МГУ, Москва

Иомдина Елена Наумовна, д.б.н, г.н.с. МНИИ глазных болезней им. Гельмгольца, Москва

Назаренко Людмила Александровна, аспирант МНИИ глазных болезней им. Гельмгольца, Москва состояние дренажной системы обследуемого пациента и не позволяют с достаточной надежностью опираться на эти показатели при выборе индивидуальной тактики лечения. В связи с этим исследования, анализирующие физическую основу тонографии и системы обработки ее результатов, а также способствующие оптимизации метода для повышения его достоверности и информативности, являются актуальными как с научной, так и с практической точки зрения.

Метод тонографии и возможные схемы обработки данных ТОНОГРАФИЧЕСКОГО ИССЛЕДОВАНИЯ

Тонография как метод оценки интенсивности оттока жидкости из глаза человека применяется как в диагностических, так и в исследовательских целях [6, 7]. Метод заключается в том, что на роговицу глаза помещается фиксированный груз и в течение длительного времени (обычно четыре минуты) измеряется изменение некоторого геометрического параметра b , характеризующего деформацию роговицы, во времени. Таким параметром может быть величина «погружения» в роговицу плунжера малого диаметра, к которому приложен груз, или площадь контакта с поверхностью роговицы плоского штампа большого диаметра. Изменение во времени деформации роговицы при ее нагружении, т.е. вид функции b = b ( t ), зависит от механических свойств оболочки глаза и внутриглазного давления, которое определяется интенсивностью процессов притока и оттока внутриглазной жидкости.

Для того чтобы на основании измеренной при тонографии величины b = b ( t ) оценить параметр, определяющий величину оттока жидкости, необходимо воспользоваться некоторой механической моделью глазного яблока, включающей, в частности, модель гидравлической системы притока и оттока внутриглазной жидкости.

Для обработки данных тонографического исследования используется простейшая механическая модель глазного яблока (рис. 1), в которой оно представляется в виде упругой оболочки объема V , заполненной несжимаемой жидкостью при давлении p и связанной с внешними системами притока и оттока.

Уравнение, описывающее изменение объема глаза, имеет вид dV

= Fh - Fe

Обычно при стандартном способе обработки тонографии считается, что величина притока жидкости в единицу времени F h не зависит от внутриглазного давления и величины нагрузки P , а величина оттока F e определяется простейшим гидравлическим соотношением

Fe = C ( P - Pe ) , где C – коэффициент легкости оттока (проводимость выводящих путей), не зависящий от внутриглазного давления и величины нагрузки на глаз; p – внутриглазное давление; pe – давление в эписклеральных венах. Примем в данном разделе те же предположения.

F h

F e

Рис. 1. Общая схема модели глазного яблока

В стационарном состоянии (до нагружения глаза при тонографии) приток жидкости равен ее оттоку:

F h = F h о = F . о = C ( P о - P . о ) .                             (3)

Здесь и далее величины, соответствующие ненагруженному состоянию, обозначены индексом 0.

Соотношение (3) определяет, в частности, внутриглазное давление p 0 в исследуемом глазу [2], если величина притока F_{h 0} известна.

Основная задача тонографии состоит в том, чтобы, используя принятую модель глаза и данные измерения, т.е. функцию b = b ( t ), оценить величину коэффициента легкости оттока C. Ясно при этом, что конкретное значение этой величины, которое получается в результате обработки данных, зависит от параметров, определяющих модель, и соотношений, связывающих функцию b = b ( t ) с параметрами модели глаза.

В отечественной медицинской практике для тонографии широко используется тонограф GlauTest –60, в программное обеспечение которого заложены некоторые эмпирические формулы, связывающие измеряемую глубину погружения плунжера b = b ( t ) с внутриглазным давлением и давление сразу после нагружения с давлением до нагружения. Принимая эти формулы, будем считать, что с помощью тонографии могут быть установлены величина внутриглазного давления до нагружения глаза тонографом p о и функция p = p ( t ) , определяющая изменение внутриглазного давления во время тонографии (при нагружении глаза грузом веса P ). Эту функцию будем называть тонограммой.

На протяжении тонографического опыта поведение оболочки глаза можно считать линейно упругим:

dV = a dp .                                   (4)

Обычно полагают, что упругое поведение оболочки не зависит от величины груза тонографа. Проведенные в настоящее время расчеты задачи о «раздувании» упругой оболочки, моделирующей глаз, показывают, что величина коэффициента объемной упругости оболочки а в диапазоне параметров, характерных для офтальмологии, слабо зависит от веса груза [4]. В связи с этим примем, что величина а не зависит от величины нагрузки при тонографии. В конкретных оценках примем в соответствии с традицией [8] соотношение а = 1 p _о 9,9215 ln19 в форме, одинаковой для всех обследуемых. Оценка индивидуальных значений а представляет собой самостоятельную задачу, которая в данной работе рассматриваться не будет.

Также обычно считается, что нагружение глаза приводит к изменению давления в эписклеральных венах на некоторую постоянную величину. При стандартной обработке для этой величины предполагается всегда одно и то же (небольшое в сравнении со стационарным значением) постоянное значение [6], мм рт. ст.:

P . = P . о + ^1,25,                                      ⁽⁵⁾

где p e – давление в эписклеральных венах в нагруженном глазу .

При сформулированных предположениях уравнение (1) с учетом (2) и (3) принимает вид а dp = C (Pо - P.о - P + P.),                           (6)

dt причем величины а, C, pо, pe - peо - постоянные, не зависящие от веса груза-тонометра. Решение этого уравнения при соответствующем подборе константы С должно совпадать с тонограммой p = p (t) для заданных а, pe - peо и pо, что дает возможность оценить коэффициент легкости оттока для конкретного обследуемого.

• 10                        ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 2 (56): 8–20

Решение уравнения (6) можно представить в виде

t

P = P , ^{1 (} P 1 - P да ) e ^T , P да = P 0 + P e - P e 0 , ^{T = a}/ C .                    (7)

Здесь p 1 = p (0) - начальное давление для тонограммы (внутриглазное давление сразу после установки груза на глаз, т.е. при t = 0), которое всегда превышает давление до нагружения p ₀ ( p 1 >  p ₀); p _да = p ( да ) - давление, которое установилось бы в глазу при неограниченной длительности нагружения; τ – характерное время изменения давления при тонографии. Таким образом, аппроксимируя тонограмму экспонентой (рис. 2) и определяя параметр т и асимптотическое значение давления при t ^да , можно, сравнивая ее с (7), оценить величину коэффициента легкости оттока С и изменение давления в эписклеральных венах при нагружении в предположении, что интенсивность притока и выходная проводимость под грузом не изменились по сравнению с разгруженным состоянием,

C = ^аД , P e ^- P e 0 = P да - P 0 .                            ⁽⁸⁾

При стандартной обработке данных тонографии (в том числе в программном обеспечении прибора GlauTest –60) величина С оценивается на основе представления тонограммы линейной функцией, причем используются для обработки только две точки (начальная и конечная) тонограммы и некоторые дополнительные предположения, не связанные с описанной выше моделью глаза [6]. Определение при предложенном авторами методе обработки дополнительного параметра тонограммы – параметра τ, характеризующего вогнутость тонографической кривой, – дает возможность найти, кроме C , еще p_e . В работе [3] содержится сопоставление результатов оценки коэффициента легкости оттока по методике GlauTest –60 и по описанной выше методике, опирающейся на соотношение (7). Расхождение оценок свидетельствует о том, что предположения, заложенные в программное обеспечение GlauTest –60, противоречат физическому смыслу принятой модели глазного яблока.

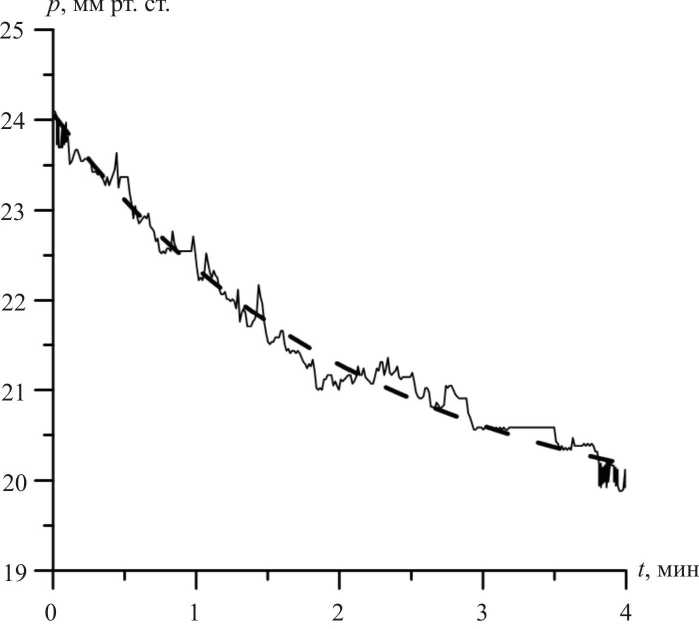
Рис. 2. Пример реальной тонограммы с аппроксимирующей ее экспонентой

Обработка данных на основе уравнения (6) не только позволяет оценить коэффициент легкости оттока, но и приводит к важным физическим выводам, которые обсуждаются в [3]. В частности, показано, что, как правило, p p 0 , т.е. в стационарном состоянии, которое установится в глазу под грузом, внутриглазное давление p „ существенно отличается от давления p 0 в ненагруженном глазу. Отсюда следует, в частности, что принимаемое обычно соотношение (5) не удовлетворяется и величина давления в эписклеральных венах должна быть включена в число определяющих параметров, зависящих от величины нагрузки на глаз. При этом естественно возникает вопрос, не могут ли и другие параметры модели ( a , C , F h ) изменяться при нагружении глаза. Эти изменения могут быть связаны с изменением внешних по отношению к глазу систем, обеспечивающих приток и отток жидкости. Отсюда следует, что измеряемые обычно при тонографии параметры модели соответствуют их значениям в стационарном нагруженном тонометром глазу и могут отличаться от соответствующих значений в ненагруженном глазу, которые представляют интерес для медицинской практики.

Таким образом, возникают вопросы о том, как нагружение глаза грузом P влияет на физические процессы в системах притока и оттока жидкости, как это влияние отражается на величинах параметров модели глаза a , C , F h , p e , как оценить значения этих параметров для глаза конкретного обследуемого и т.д.

В данной работе будет описан и обоснован модифицированный (усложненный) метод тонографии, позволяющий оценить при некоторых допущениях значения параметров C ₀ , F_{h 0} , p_{e 0} для ненагруженного глаза и их же значения C , F_h , p _e для глаза под нагрузкой, а также будут приведены результаты использования этого метода при обследовании пациентов в клинике.

Модифицированный метод тонографии

Прежде всего сформулируем некоторые предположения. В [3] показано, что условия F h = F h 0 , C = C 0 , p e = p e 0 не могут удовлетворяться одновременно (этот вывод проиллюстрирован выше), т.е. параметры, характеризующие глазное яблоко и процессы притока и оттока жидкости, все или частично, могут зависеть от величины приложенной нагрузки P и, вообще говоря, от внутриглазного давления, которое изменяется под воздействием груза. Какие физические механизмы обеспечивают изменение параметров глаза под нагрузкой или в других нестационарных процессах в глазу, в настоящее время неизвестно. Тем не менее если интересоваться некоторыми средними значениями этих параметров при тонографии, увеличении объема глаза при введении лекарств или в других нестационарных процессах, то можно воспользоваться описанной выше моделью глаза, подразумевая под соответствующими величинами их средние значения за время исследуемого нестационарного процесса. Подчеркнем, что при этом конкретная зависимость физических процессов, определяющих приток и отток жидкости, от нагружения глаза остается неизвестной.

Внутриглазное давление при нагружении глаза изменяется практически мгновенно (за время ~ 1 с). Как быстро при нагружении глаза изменяются условия производства внутриглазной жидкости (водянистой влаги) и гидравлическое сопротивление путей оттока жидкости, неизвестно. В данной работе будем предполагать, что средние значения всех физических параметров, определяющих приток и отток жидкости ( C , F h , p e , а ) и, возможно, изменяющихся при нагружении глаза, изменяются практически мгновенно при нагружении и остаются неизменными все время, пока глаз находится под нагрузкой . Кроме того, примем, что эти величины не зависят явно от внутриглазного давления. Это означает, что параметры модели глаза 12 ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 2 (56): 8–20

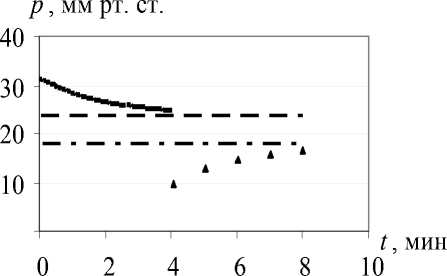
Рис. 3. Схема измерений при модифицированной тонографии: давление под нагрузкой – сплошная линия, восстановление давления после снятия груза – треугольники (пунктиром обозначено p ∞ , штрих-пунктиром – p 0 )

могут быть различными в нагруженном и ненагруженном глазу, но их значения остаются неизменными во время тонографии, хотя и, возможно, зависящими от величины P . Сформулированные предположения правомерны, если зависимость всех упомянутых величин от давления p намного слабее, чем характеризуемая коэффициентом C зависимость от p скорости оттока. В противном случае от параметров функций, определяющих эти зависимости, будет зависеть характерное время изменения давления.

Согласно современным представлениям [6] величина давления в эписклеральных венах в обычных стационарных условиях у разных людей меняется в небольших пределах p e 0 ~ 8 - 10 мм рт. ст. В связи с этим при конкретных расчетах примем p e 0 = 8 мм рт. ст., а давление в эписклеральных венах под нагрузкой будем рассчитывать в соответствии с соотношением (5) .

Описанные выше предположения относятся к способу обработки данных тонографического исследования. Само же исследование предлагается проводить следующим образом. Сначала выполняется обычная тонография. При этом глаз находится под нагрузкой в течение 4 минут. При t = 0 (в момент нагружения глаза плунжером тонометра) внутриглазное давление изменяется «скачком» от p 0 до величины p 1 . Затем в течение 4 минут давление в глазу понижается за счет дополнительного оттока жидкости из глаза. В конце процедуры тонографии ( t = 4 мин) давление равно некоторому значению p 2 <  p 1 , причем, как указывалось выше, практически всегда p ₂ >  p 0 . При этом на плоскости p , t получаем стандартную тонограмму (сплошная линия на рис. 3). Когда груз снимается с глаза, в нем «скачком» устанавливается давление p ₂₁ <  p 0 (рис. 3).

Модификация тонографии заключается в том, что сразу после стандартной тонографии (при t > 4 мин) выполняется дискретное измерение внутриглазного давления (тонометрия) в течение достаточно большого времени. Желательно, чтобы измерение давления в процессе тонометрии осуществлялось тем же тонометром, что и при тонографии. В результате такой тонометрии регистрируется изменение внутриглазного давления в нестационарном процессе восстановления стационарного состояния глаза после тонографии ( p ^ p 0 ). Этот процесс (представлен символами на рис. 3) на практике продолжается 10–20 мин, что позволяет получить достаточное количество точек для их аппроксимации и соответствующей обработки. Обратим внимание на то, что согласно принятому выше предположению о мгновенном изменении средних параметров при нагружении или разгрузке глаза вслед за снятием груза давление в эписклеральных венах также должно мгновенно изменяться от p e до значения p e 0 .

Обработка результатов модифицированной тонографии

Поскольку первая часть исследования представляет собой стандартную тонографию, то ее обработка производится так, как описано выше, и определяются значения величин т , p ^ . При этом вместо (6) используются уравнения (1) и (2), результатом применения которых является следующее выражение:

a dp = F — C ( Р — P e ) .                            (9)

dt

Используя его решение типа (7), аналогично (8) получаем:

C = У_т , F = C ( P . - P e ) .                       (10)

В соотношениях (9)–(10) величина p e представляет среднее за время тонографии давление в эписклеральных венах в нагруженном глазу.

Обрабатывая вторую часть исследования (груз отсутствует), поступаем аналогичным образом. Исходим из того, что началу этого участка зависимости p = p (t) соответствует t2 = 4 мин, давление в этой точке p = p21 (см. рис. 3) и что p ^ p0 при t >да. Вместо (7) используем решение уравнения (1) с учетом (2) и (4) в виде p = pо +(p21 - pо) e ' t-t2 )Ao.                                  (11)

Аппроксимируя набор значений давления при t > t2 (см. рис. 3) экспонентой и сопоставляя эту экспоненту с решением (12), получаем со = % • Fо = C(pо - p.о)•                         (12)

то где τ0 – характерное время изменения давления для экспоненты, аппроксимирующей опытные данные при P = о, которое оценивается из сопоставления экспериментальной кривой p = p (t, P = о) с соотношением (11).

Таким образом, при реализации метода модифицированной тонографии однозначно определяются средние значения коэффициентов легкости оттока C 0 и C для данного обследуемого, если известна величина константы объемной упругости a . Для определения же величин среднего притока под нагрузкой F h (10) и оттока F e в каждый момент времени при тонографии (2) необходимо задаться величиной среднего давления в эписклеральных венах под нагрузкой p e либо каким-то еще соотношением, связывающим величины C ₀, C , F_h , F_{h 0}, p_e .

Для того чтобы оценить возможности метода модифицированной тонографии и следствия, к которым приводят те или иные описанные выше предположения, связанные с обработкой данных тонографии, были выполнены исследования ограниченной группы пациентов.

Материал экспериментального исследования

В работе проанализированы результаты тонографического обследования 27 пациентов (27 глаз) в возрасте 22–80 лет (средний возраст 61,8±2,6 г.), в том числе 15 пациентов с I–III стадиями первичной открытоугольной глаукомы, часть из которых находилась на медикаментозном гипотензивном режиме, а также 3 пациентов с подозрением на первичную открытоугольную глаукому и 9 пациентов, не страдающих глаукомой и другими заболеваниями глаз. Ниже приводятся таблицы с результатами обследования 10 из этих пациентов.

Результаты и их обсуждение

В табл. 1 для каждого обследуемого приведены фактические данные исследования: p 0 – внутриглазное давление перед началом исследования; τ, τ 0 – характерные времена изменения давления в нагруженном и ненагруженном глазу; p _ю -стационарное значение давления в нагруженном глазу; C , C ₀ – средние коэффициенты легкости оттока в нагруженном и ненагруженном глазу; F e 0 = F h 0 - величины стационарного оттока и притока в ненагруженном глазу (при их вычислении принято, что p e 0 = 8 мм рт. ст.). Для всех обследованных при вычислении этих параметров по формулам (10) и (11) использовалось выражение а = ( 0,0215 p ₀ln10 ) . В этой же таблице приведены значения отношения характерных времен без нагрузки и под нагрузкой т ₀ / т , которое в соответствии с принятой моделью равно отношению средних коэффициентов легкости оттока: С/С ₀ = т ₀ / т .

Непосредственно из приведенных в таблице данных видно, что это отношение, как правило, существенно больше единицы (у большинства обследованных оно находится в диапазоне 3...10) и сильно варьирует. Это означает, что характерное время восстановления давления после разгрузки намного превосходит время его установления после нагружения (и в соответствии с моделью коэффициент легкости оттока под нагрузкой во столько же раз больше того же коэффициента при отсутствии нагрузки).

Вычисление параметров, значения которых приведены в табл. 1, требует задания только величины константы упругости а и давления в эписклеральных венах до нагружения глаза – p_{e 0} . Для оценок же средних величин притока и оттока под нагрузкой необходимо, как уже упоминалось, сделать предположения относительно изменения величины давления в эписклеральных венах p_e или принять какие-то дополнительные гипотезы, устанавливающие связь между параметрами C , C 0 , F h , F h 0 , p e , p e 0 .

Если принять, как это делается практически всегда при обработке данных тонографии, соотношение (5) для величины изменения давления в эписклеральных венах под нагрузкой p e = p e ₀ + 1,25 мм рт. ст., то легко оценить для каждого обследуемого величины притока жидкости под нагрузкой F_h и равные им величины

Таблица 1

Результаты обработки модифицированного тонографического исследования

№ п/п p0 p∞ τ τ0 τ0/τ = C/C0 C C0 Fh0 = Fe0 1 12 20,5 1,33 4,2 3,2 1,26 0,4 1,6 2 12 22,1 0,72 5,8 10,7 3,1 0,29 1,16 3 16 18,7 2,8 5,2 1,9 0,45 0,24 1,92 4 13 21,2 3,35 16,4 4,8 0,43 0,09 0,45 5 16 24 4,18 5,4 1,9 0,44 0,23 1,84 6 14 26,3 1,7 7,3 4,1 0,82 0,2 1,2 7 9 18,4 2,88 7,5 2,3 0,7 0,3 0,3 8 17 24,4 1,6 3,2 2 0,74 0,37 3,33 9 17 27,7 3,23 12,4 3,7 0,37 0,1 0,9 10 12 16,3 6,2 3,3 0,7 0,35 0,48 1,92 оттока жидкости в стационарных условиях Feю = C (p, pe). Эти величины даны в табл. 2, где для удобства приведены также значения параметров C0, C, C0/С, Fh0 = Fe0, взятые из табл. 1, а также отношение Fh0 /Fh = Fe0 (Feх .

Обращает на себя внимание тот факт, что при описываемой обработке данных модифицированной тонографии средние величины коэффициента легкости оттока C и притока F_h при нагружении глаза возрастают, причем величина притока F_h очень сильно.

Такое увеличение притока жидкости в глаз под нагрузкой трудно объяснить, имея в виду существующие представления о механизмах «производства» жидкости (водянистой влаги) в глазу. С другой стороны, величины притока F_h и оттока F_e в стационарном режиме существенно зависят от величины давления в эписклеральных венах p_e , которая при оценке данных табл. 2 считалась в соответствии с допущением (5) практически не зависящей от нагружения глаза ( p e = p e ₀). Таким образом, вопрос об изменении величин притока и оттока жидкости при нагружении глаза оказывается связанным с вопросом об изменении давления в эписклеральных венах.

Поэтому рассмотрим другой крайний вариант. Примем, что приток жидкости в глазу не зависит от его нагружения или разгрузки, и проанализируем, к каким следствиям приводит данное предположение в рамках принятой механической модели глаза. В этом случае условие равенства равновесных значений притока в нагруженном и ненагруженном глазу

C ( p»— pe ) = C0 ( p 0 - pe 0 )

может удовлетворяться только в том случае, когда давление в эписклеральных венах изменяется при нагружении глаза, причем pe = p»- CT ( p 0 - pe 0 ) , т.е., принимая предположение о равенстве притоков, необходимо отказаться от предположения о том, что pe = pe0. Несовместимость этого допущения с данными измерений была показана авторами ранее уже при анализе только стандартной тонографической процедуры (см. выше).

Таблица 2

Результаты обработки модифицированного тонографического исследования в предположении независимости давления в эписклеральных венах от нагружения глаза

№ п/п	τ	τ 0	τ 0 /τ	C	C 0	F h 0 = F e 0	F h = F e ∞	F h / F h 0
1	1,33	4,2	3,2	1,26	0,4	1,6	14,175	8,8
2	0,72	5,8	10,7	3,1	0,29	1,16	39,835	34,3
3	2,8	5,2	1,9	0,45	0,24	1,92	4,2525	2,2
4	3,35	16,4	4,8	0,43	0,09	0,45	5,1385	11,4
5	4,18	5,4	1,9	0,44	0,23	1,84	6,49	3,8
6	1,7	7,3	4,1	0,82	0,2	1,2	13,981	11,6
7	2,88	7,5	2,3	0,7	0,3	0,3	6,405	21,3
8	1,6	3,2	2	0,74	0,37	3,33	11,211	3,4
9	3,23	12,4	3,7	0,37	0,1	0,9	6,8265	7,6
10	6,2	3,3	0,7	0,35	0,48	1,92	2,4675	1,3

Таким образом, следствием предположения о независимости притока жидкости от нагрузки является то, что при неограниченно продолжающейся тонографии ( P * 0, t ^« ) в глазу устанавливается такое давление p ^ , которое обеспечивает при коэффициенте легкости оттока С , устанавливающемся в нагруженном глазу, отток жидкости, равный оттоку F e 0 в стационарном состоянии, имевшем место до начала тонографии (при p = p 0 ). Отсюда следует, что величина p ^ оказывается тесно связанной с величиной изменения давления в эписклеральных венах при нагружении. Какие физические механизмы ответственны за эту связь, каким образом нагружение глаза влияет на давление в эписклеральных венах, как быстро происходит изменение этого давления – все эти вопросы нуждаются в дополнительном исследовании.

В табл. 3 для всех обследованных приведены величины F h = F e 0 и p e , полученные в результате обработки усложненного тонографического исследования с учетом предположения о независимости притока от нагрузки и соответствующего изменения давления в эписклеральных венах.

Разница в значениях одних и тех же величин, приведенных в табл. 2 и 3, связана с различием в обработке данных одного и того же модифицированного тонографического исследования. Невольно возникает естественный вопрос о том, какой же из этих двух (или, возможно, еще других) способов обработки тонографического исследования является более обоснованным с физической точки зрения. Этот вопрос не имеет сегодня однозначного ответа.

Пусть нас интересует только величина коэффициента легкости оттока, определенная соотношением (2) в принятой механической модели глаза. В этом случае, выполнив модифицированное тонографическое исследование, можно оценить значение этого параметра по формулам (10) и (12) для нагруженного и ненагруженного глаза. При этом необходимо принять (или определить для данного обследуемого) величину объемного модуля упругости а . В настоящее время при обработке данных тонографии используется одинаковая для всех обследуемых зависимость, дающая при линеаризации а = 1 P 0 0,0215ln10 . Если стремиться учесть индивидуальное значение упругого модуля, то необходимо дополнительно к тонографии определить эту величину для данного обследуемого, например, сделав ему дифференциальную тонометрию (измерение внутриглазного давления при кратковременном нагружении глаза последовательно двумя разными грузами).

Однако надо иметь в виду, что для оценки величины оттока жидкости из глаза необходимо знать не только коэффициент легкости оттока, но и давление в эписклеральных венах. Если для ненагруженного глаза принять, что давление p_{e 0} у разных обследуемых меняется в пределах 8–10 мм рт. ст., то при p 0 = 15 мм рт. ст. можно ожидать ошибки в оценке величины оттока порядка 30%. Величина этой ошибки зависит от принятого для оценки значения p_{e 0} и от внутриглазного давления.

Что касается нагруженного глаза, то вопрос упирается в оценку величины p_e и ее зависимости от величины нагрузки и индивидуальных особенностей глаза обследуемого.

Таблица 3

Результаты обработки модифицированного тонографического исследования в предположении о независимости притока от нагрузки

Показатель	№ п/п
	1	2	3	4	5	6	7	8	9	10
p e	19,2	21,6	14,4	20,2	14,4	0,5	18	19,9	25,3	8,8
F h = F e 0	1,6	1,2	1,9	0,5	1,7	1,2	0,3	3,3	0,9	1,9

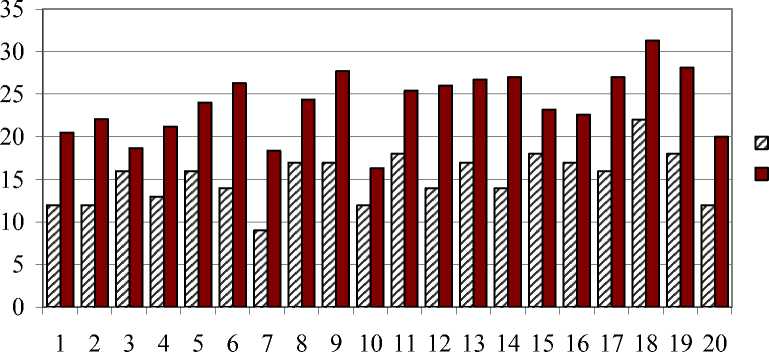
p 0 p ∞

Рис. 4. Индивидуальные различия между p 0 и p ∞ (мм рт. ст.) для 20 обследованных

Эти же проблемы возникают и при оценке величины притока жидкости к глазу и его зависимости от нагрузки. Выше указывалось, что при независимости притока жидкости от нагрузки давление p e определяет значение давления p „ , которое устанавливается в глазу при тонографии за неограниченное время ( P * 0, t ^ да ) . Поэтому возможно, что p _да может служить некоторой мерой процессов, приводящих к изменению давления в эписклеральных венах при нагружении глаза. Величина p _да легко определяется при обработке данных тонографии и, как видно из рис. 4, существенно зависит от индивидуальных особенностей обследуемых. В связи с этим представляет, по-видимому, интерес изучение связи величины p _да (или p _да- p 0 ) с индивидуальными особенностями обследуемых глаз (характером или тяжестью заболевания). Если такая связь будет установлена, то величина p _да сможет служить диагностическим параметром, характеризующим состояние гидродинамики глаза пациента в момент его обследования.

Оценка коэффициентов легкости оттока C и C 0 показывает (см. табл. 1, 2), что эта величина возрастает при нагружении глаза. В настоящее время не ясно, какие физические механизмы ответственны за этот рост. Так как при нагружении глаза возрастает внутриглазное давление, то, возможно, возрастание коэффициента легкости оттока является отражением того факта, что закон сопротивления оттоку жидкости (2) в действительности нелинеен по давлению, т.е. C = C ( p ) . Возможно также, что выходное давление p_e определяется собственными динамическими соотношениями. Однако обсуждение всех этих вопросов выходит за рамки данной работы.

Заключение

В настоящее время для оценки гидравлического сопротивления дренажной системы глаза пользуются простейшей механической моделью глазного яблока, описанной в начале данной работы. Эта модель в стационарном состоянии определяется четырьмя параметрами – давлением в ненагруженном глазу p ₀ , а также величинами a , C , p e , которые предполагаются не зависящими от состояния глаза в любом нестационарном процессе, связанном с его раздуванием, нагружением, деформацией и т.д. (для p_e иногда допускается несущественное фиксированное увеличение под нагрузкой). Предполагается, что существует некоторая система опытов и оценок, 18 ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 2 (56): 8–20

позволяющая для конкретного обследуемого оценить индивидуальные значения параметров a , p 0 , p e . Поэтому для оценки свойств гидравлической системы глаза на основе принятой модели достаточно оценить только значение коэффициента легкости оттока C . Для этой цели и был разработан метод тонографии, в котором величина C оценивается на основе использования внутриглазного давления в нестационарном процессе, возникающем после нагружения глаза некоторым грузом.

Однако, как показывают описанные выше результаты обработки данных стандартной тонографии и предложенного авторами модифицированного метода тонографии, механические свойства и параметры глаза как системы, моделируемой принятой механической моделью, существенно различаются для нагруженного и ненагруженного глаза. Если принять закон сопротивления оттоку (2) и считать, что параметры F_h , C , p_e , характеризующие модель, изменяются при нагружении или разгрузке глаза скачком (мгновенно), то можно считать доказанным, что коэффициент легкости оттока C и давление p ∞ , устанавливающееся в глазу в стационарном состоянии (при t ^ю ), возрастают при нагружении глаза. Эти величины для нагруженного ( C , p ∞ ) и ненагруженного ( C 0 , p 0 ) глаза, а также величина оттока жидкости в ненагруженном глазу F e = C 0 ( p 0 - p e 0 ) могут быть определены с помощью модифицированного метода тонографии при известных параметрах p ₀, p_{e 0} .

Как кажется авторам, представляет безусловный интерес с точки зрения офтальмологии оценка с помощью метода модифицированной тонографии параметров системы оттока жидкости в естественном ненагруженном состоянии и оценка диагностической значимости получаемых при этом величин.

Однако для окончательного обоснования модифицированной тонографии как метода определения параметров ненагруженного глаза необходимы физиологические и механические исследования нестационарных процессов, возникающих в глазу при его нагружении или разгрузке и определяющих характерные времена изменения величин F h , C , p e .

Эти же исследования, наряду с оценкой параметров ненагруженного глаза, будут полезны для получения более полных представлений о функционировании систем притока и оттока внутриглазной жидкости. В этой связи обращает на себя внимание отмеченная связь параметра p ∞ с изменением давления в эписклеральных венах при нагружении глаза. Весьма вероятно (но нуждается в экспериментальном подтверждении), что величина p ∞ окажется удобным диагностическим параметром, отражающим индивидуальные изменения в дистальном отделе дренажной системы глаза.

Благодарности

Работа выполнена при поддержке РФФИ (проект № 11-01-00774).