Об одной гипотезе теории формальных языков. Часть I
Автор: Мельников Б.Ф.
Статья в выпуске: 3 т.12, 2023 года.
Бесплатный доступ
Основной предмет статьи - рассмотрение задач, возникающих при исследовании необходимых условий равенства бесконечных итераций конечных языков. В предыдущих публикациях автором рассматривались примеры применения соответствующего этому равенству специального бинарного отношения эквивалентности на множестве конечных языков, причем рассматривались как примеры, описывающие необходимые условия его выполнения, так и примеры его использования. К одному из таких необходимых условий применены два варианта сведeния рассматриваемой задачи: к конечным автоматам и к бесконечным итерационным деревьям. Также в статье приведены несколько вариантов важной гипотезы, формулируемой для множества конечных языков; ее исследование дает и иные варианты сведeния рассматриваемой задачи к специальным задачам для недетерминированных конечных автоматов. При этом в случае выполнения сформулированной гипотезы некоторые из таких задач решаются за полиномиальное время, а некоторые не решаются; при продолжении работ по данной тематике последний факт может дать возможность переформулировки проблемы P = NP в виде специальной задачи теории формальных языков.
Формальные языки, итерации языков, бинарные отношения, морфизмы, инверсные морфизмы, алгоритмы, полиномиальные алгоритмы
Короткий адрес: https://sciup.org/147241763
IDR: 147241763 | УДК: 519.766, | DOI: 10.14529/cmse230305
Текст научной статьи Об одной гипотезе теории формальных языков. Часть I
Некоторые результаты предлагаемой работы уже были опубликованы, причем относительно недавно, в 2019 г. и позднее — см. [1 –12] . Однако их желательно повторить (с добавлениями и изменениями) — по следующим причинам.
\bullet Во-первых, необходима публикация на эту тематику именно в журнале, тематика которого в большей степени связана с прикладной математикой: в упомянутых выше публикациях большее внимание уделялось связи с теоретической информатикой 1 .
\bullet Во-вторых, приводятся подробные обозначения для применяемой в статье версии недетерминированных конечных автоматов (соответствующие определения и простейшие утверждения). Эти обозначения для конечных автоматов на русском языке уже были опубликованы — но в полном объеме лишь в монографии, [13] .
\bullet В-третьих, немного по-другому описываются результаты статьи [14] (1993 г.) — где было приведено неполное доказательство одного из рассматривавшихся там утверждений.
\bullet В-четвертых, хотя настоящую работу можно назвать обобщающей, — но в нее автор постарался включить только такой минимум из материала ранее опубликованных статей, который необходим для понимания рассматриваемых проблем. Здесь под этим минимумом в первую очередь понимается то, что необходимо для плана сведения равенства P = NP (гипотезы P = NP) к специальной гипотезе теории формальных языков.
\bullet Однако при этом («в-пятых»), такой минимально возможный объем материала отражает не только сами результаты работы, но и связь с другими ранее рассматривавшимися задачами. Более того, как автор надеется, при такой подаче, которая применена в настоящей обобщающей статье, более понятна мотивация к рассмотрению вспомогательных задач — а эту мотивацию при простом чтении в хронологическом порядке статей [1 –12] можно и не увидеть.
\bullet В-шестых, в настоящей статье добавлены некоторые новые результаты, полученные в последнее время.
\bullet Однако самой важной является следующая причина («в-седьмых»): существенно изменяется сама структура изложения. А именно, в упомянутых выше работах основной целью было решение соответствующих вспомогательных задач, в частности — описание возможных полурешеток, полученных на основе двух заданных конечных языков, а также описание применения результатов, связанных с этими полурешетками, в прикладных задачах теории языков. А у настоящей статьи цель более глобальная, и поэтому приводится:
– подробное описание самих рассматриваемых задач;
– описание нескольких гипотез, возникающих для специальных множеств формальных языков (иными словами — для подмоноидов глобального надмоноида свободного моноида, [15] );
– а также связь этих задач с упомянутой выше проблемой P = NP.
Все упомянутые выше задачи связаны с исследованием бинарного отношения эквивалентности в бесконечности, заданного на множестве конечных языков, — отношения \leqslant\geqslant| . В предыдущих публикациях уже были рассмотрены примеры применения как этого отношения, так и его частного случая — отношения \leqslant| ; при этом примеры можно разделить на две группы:
\bullet примеры, описывающие необходимые условия его выполнения;
\bullet и примеры его использования — в различных областях теории формальных языков, дискретной математики и абстрактной алгебры.
Из сказанного выше следует, что основным предметом статьи можно считать рассмотрение разных задач, возникающих при исследовании необходимых условий равенства бесконечных итераций конечных языков (иными словами — условий выполнения бинарного отношения \leqslant\geqslant| ). И, по-видимому, главной «составляющей» такой мотивации является план доказательства возможности сведения равенства P = NP к специальной гипотезе теории формальных языков, сформулированной ранее в предыдущих публикациях. Стоит отметить по этому поводу, что первая версия этого плана была опубликована в 2011 г., см. [16] — а здесь приведена измененная версия, причем со значительно большим числом комментариев. Однако основная идея при этом та же самая — но здесь она уже оформлена конкретно, и решения многих вспомогательных подзадач, необходимых для осуществления указанного плана, за прошедшее время уже опубликованы.
Кратко этот план можно сформулировать следующим образом. По некоторому недетерминированному конечному автомату специальным образом строится пара конечных языков — и для этой пары показывается, что если бы была выполнена вышеупомянутая гипотеза, то существовал бы и алгоритм проверки выполнения отношения эквивалентности в бесконечности за полиномиальное время. Но, с другой стороны, взяв произвольный недетерминированный конечный автомат и рассматривая его как определенный в предыдущих публикациях т. н. автомат NSPRI (мы его строго определим и будем рассматривать начиная с раздела 6 настоящей статьи), мы за полиномиальное время могли бы построить соответствующую этому автомату пару конечных языков — причем такую пару, которая удовлетворяет отношению \leqslant|\geqslant тогда и только тогда, когда язык автомата NSPRI совпадает с универсальным языком над заданным алфавитом (т. е. языком, содержащим все возможные слова). Таким образом, в случае осуществления плана, кратко описанного здесь, мы покажем, что выполнение вышеупомянутой основной гипотезы влечет выполнение равенства P = NP.
В конце данного раздела отметим следующее. Мы всюду пишем «сведение равенства P = NP к одной из гипотез теории формальных языков» (и т. п.) – но, по-видимому, еще точнее было бы говорить «сведение гипотезы P = NP к одной из гипотез теории формальных языков»; однако последний вариант звучит хуже (из-за двух вхождений слова «гипотеза»). На сказанное здесь можно было бы возразить, что любая (или почти любая) вычислительная проблема может рассматриваться именно как проблема теории формальных языков (см. [17, 18] и мн. др.); однако «возражение на возражение» заключается в том, что для получения необходимой информации нужно решить только одну проблему, или, другими словами, здесь речь идет о формулировке задачи про задачи, можно сказать — «о формулировке метазадачи».
Следует также особо отметить, что даже после возможного завершения реализации плана, приведенного вышу, о возможности решения проблемы P = NP ничего утверждаться не будет: будет показана только возможность сведения этой проблемы к проблеме теории формальных языков.
Приведем содержание статьи по разделам.
В разделе 1 приводятся основные обозначения и обсуждаются соглашения об их использовании; некоторые из этих обозначений являются нестандартными. Одним из наиболее важных понятий, определенных в этом разделе, является бинарное отношение \leqslant|\geqslant , определенное на множестве конечных языков над рассматриваемым алфавитом; можно сказать, что с этим бинарным отношением связан весь материал настоящей статьи.
В разделе 2 рассматриваются бесконечные деревья особого вида , которые возникают в различных задачах теории формальных языков. Отличительной особенностью этих деревьев является то, что все их ребра отмечены буквами заданного алфавита, а вершины делятся на некоторые классы эквивалентности, причем (бесконечные) поддеревья, соответствующие вершинам одного и того же класса, эквивалентны . Разделом 2 заканчивается часть I настоящей статьи, последующие разделы составят части II–IV.
В разделе 3 обсуждается несложное преобразование , строящее по заданному бесконечному итерационному дереву специальный детерминированный конечный автомат. При этом с точки зрения алгебры мы переходим от работы с элементами определенного множества к работе с классами эквивалентности , на которые это множество делится с помощью бинарного отношения, фактически рассмотренного в предыдущем разделе 2.
Таким образом, в разделе 3 рассматривается общий (абстрактный) вариант преобразования произвольного бесконечного итерационного дерева в детерминированный конечный автомат; а в разделах 4 и 5 — конкретное дерево, получаемое не «абстрактно», как в разделе 3 и ранее, а специально описанным образом по двум заданным конечным языкам; соответственно, получается связанный с этими языками детерминированный автомат. Эти дерево и автомат предназначены для проверки упомянутого выше бинарного отношения \leqslant|\geqslant ; точнее, используется другое бинарное отношение \leqslant| , двойное применение которого и дает требуемое отношение \leqslant|\geqslant .
В разделе 6 описывается совершенно иной объект (теперь — недетерминированный конечный автомат) — хотя при этом стоит отметить, что построение этого автомата может быть выполнено с использованием тех же самых алгоритмов (и соответствующих компьютерных программ, [5, 6] ), что и для предыдущего раздела. Итак, в разделе 6 рассматривается недетерминированный автомат, отвечающий на тот же самый вопрос . Важно отметить, что последний автомат определен на конечном множестве слов — а не на конечном множестве языков (конечных множеств слов).
В разделе 7 и последующих разделах рассматривается специальная гипотеза теории формальных языков , которую автор считает очень важной; по ней и названа вся статья. Очень кратко эту гипотезу можно сформулировать следующим образом: бесконечные итерации конечных языков одинаковы тогда и только тогда, когда эти языки могут быть представлены как один и тот же морфизм расширенных максимальных префиксных кодов, определенных над некоторым вспомогательным алфавитом (едином для обоих языков). Непосредственно в разделе 7 рассматриваются результаты предыдущих публикаций, относящиеся к упомянутой гипотезе в частности и к материалу настоящей статьи вообще. Далее в разделе 8 рассматриваются несколько основных вариантов формулировки этой гипотезы — а именно, такие варианты, которые не использующие автоматы и деревья.
В разделе 9 кратко обсуждаются недетерминированные конечные автоматы особого вида — так называемые лепестковые автоматы (иногда в английской литературе встречается термин “semiflower automata”). Мы приводим результаты одной из предыдущих работ, эти результаты можно сформулировать следующим образом: для любого регулярного языка и его таблицы бинарного отношения # (подробнее об этом отношении см. раздел 1) существует алгоритм построения лепесткового автомата, имеющего либо ту же самую таблицу, либо ее же с ровно одним добавленным столбцом (т. е. с ровно одним добавленным состоянием канонического автомата для зеркального языка). Конкретно в настоящей статье лепестковые автоматы используются для еще двух переформулировок основной рассматриваемой в статье гипотезы — см. раздел 10 . Поэтому название раздела 10 таково: «Вспомогательные варианты формулировки гипотезы — с использованием автоматов и деревьев». Для таких вариантов и используются лепестковые конечные автоматы, а также бесконечные итерационные деревья.
Упомянутый выше план сведения равенства P = NP к более простой формулировке приведен в разделе 11 . Более детальное название этого раздела могло бы быть таким: «О плане доказательства возможности сведения равенства P = NP к гипотезе теории формальных языков».
Последний раздел — заключение; в нем формулируются возможные направления дальнейших работ по тематике настоящей статьи.
-
1. Предварительные сведения
В этом разделе приводятся основные обозначения и соглашения об их использовании. Следует отметить, что некоторые из этих обозначений являются нестандартными. Одним из наиболее важных понятий, приводимых в этом разделе, является бинарное отношение <^ , определенное на множестве конечных языков над рассматриваемым алфавитом, с ним связан весь материал этой статьи. Перейдем к самим обозначениям.
Чаще всего слова и языки будут рассматриваться над главным алфавитом Σ; вспомогательным же алфавитом обычно будет ∆, иногда с нижними индексами; все алфавиты всегда конечны.
Для заданного слова u \in Σ \ast и языка A \subseteq Σ \ast :
-
• язык pref (u) - это множество префиксов слова u (включая само u);
-
• opref (u) = pref (u) \ { u } ;
-
• pref(A) = U pref(u);
u \in A
-
• opref (A) определяется аналогично.
Если для двух конечных языков A и B (в предыдущих работах они чаще всего рассматриваются над главным алфавитом Σ) выполняется условие
(Vu E A*) (3v E B*) (u E opref(v)), то будем писать A ^ B (либо B ^ A). Если условия A ^ B и A ^ B выполняются одновременно, то будем писать A \leqslant\geqslant B.
(Специально отметим еще раз разницу в обозначениях: с одной стороны, в недавних работах [1 –12] , и с другой стороны, в [14] и некоторых других работах 1990-х годов. Конечно, в настоящей статье будут использоваться только обозначения, приведенные в этом разделе.)
Теперь приведем некоторые обозначения, связанные с недетерминированными конечными автоматами. Пусть
K = ( Q, £, 5, S, F ) (1)
— некоторый автомат. 5 — его функция переходов вида 5 : Q х £ ^ Р (Q), где обозначение Р (Q) обозначает надмножество (степень множества, множество подмножеств) множества
Q; таким образом, будут рассматриваться только автоматы без ε-переходов. Иногда некоторая дуга графа переходов автомата 5(q,a) Э т будет записываться в виде q—^т, или, если это не вызывает неоднозначности, просто в виде q-a→r.
Зеркальный автомат для автомата (1) , т. е
Q,Σ,δ R ,F,S , где q \prime - a → q \prime\prime δ R
тогда и только
тогда, когда q \prime\prime - a δ → q \prime , будем обозначать K R ; заметим, что K R всегда определяет зеркальный язык L R .
Для рассматриваемого языка L его канонический автомат будет обозначаться записью L. Пусть автоматы L и L R для заданного регулярного языка L таковы:
L = (Q n ,£,5 n , ЫЛ) и L R = (Q p ,Z,5 p , { s p } ,F p) .
Более того, для языков конечных автоматов не будет допускаться возможность L = 0 , поэтому оба этих автомата действительно имеют стартовые состояния (т. е. приведенные обозначения не могут содержать противоречия).
Для автомата (1) выходной язык состояния q (он обозначается записью L K ut (q) ) — это язык автомата ( Q, L, 5, { q } ,F). Аналогично, входной язык состояния q (обозначается L K^q)) — это язык автомата ( Q, L, 5, S, { q}).
Также напомним определение бинарного отношения # , подробнее см. [19] и др. Отношение * С Q n х Q p определяется для пар состояний автоматов L и L R следующим образом: A # X тогда и только тогда, когда
( 3 uv е L ) ( u е £ "■ (A), v R eL ^R (X) )
(в последней записи для каждого из канонических автоматов применено обозначение входного языка состояния). Важно отметить, что именно такой вариант определения неконструктивен; однако, например, [19] содержит эквивалентный конструктивный вариант подобного определения (однако, как обычно в подобных ситуациях, более сложно формулируемый).
Важно также отметить, что детерминированные конечные автоматы всегда рассматриваются как частный случай недетерминированных автоматов , определенных в соответствие с (1) , — аналогично большинству источников, но в отличие, например, от [20] . В статье не приводятся более подробные определения для детерминированных автоматов, они являются более-менее стандартными; отметим только, что будут специально использоваться так называемые всюду определенные автоматы (“total automata”), т. е. такие, для которых выполняется следующее условие:
( V q е Q ) ( V a е L ) ( | S(q,a) | = 1 ) .
В то же время во многих публикациях подобная такая «полнота» даже рассматривается в качестве обязательного свойства детерминированного автомата — однако в настоящей статье применяется другой подход, т. е. всюду определенные автоматы рассматриваются в качестве собственного подмножества автоматов детерминированных. В настоящей статье будут использоваться и так называемые лепестковые конечные автоматы (“semiflower automata”); подробности см. в разделе 10, где кроме них определены еще и автоматы типа ^ (A) для заданного конечного языка A С L * . Дополнительная информация о связанных с такими автоматами обозначениях приведена в [21] .
Перейдем к специальным обозначениям, связанным с морфизмами языков. Для этого сначала специально отметим, что все рассматриваемые конечные языки не являются пустыми и не содержат пустого слова ε. Для некоторого языка
(не ограничивая общности можно предполагать, что слова языка каким-то образом упорядочены), мы рассматриваем алфавит Д а = { d i , d 2 ,... dn } (если это не вызывает неоднозначности, обычно пишем просто ∆). Для этого алфавита рассматривается морфизм вида h A : Д А ^ L * , определенный следующим образом:
h A (d l ) = U 1 , h A (d 2 ) = U 2 , . . . , h A (d n ) = U n .
При этом мы, как обычно, для каждого слова d1 d2 . . . dn \in ∆\ast предполагается, что h(di d2 ... dn) = h(di) h(d2)... h(dn).
Однако, как может быть понятно из введения, предмет настоящей статьи связан (частично) с более важной и более сложной проблемой (т. е. более сложной, чем построение морфизма), а именно — с проблемой построения инверсного морфизма. Отметим, что в [8 –10] приведено только начало рассмотрения этой проблемы.
Сформулируем его определение более подробно. Во-первых, дадим такое естественное определение. Для данного конечного языка A, морфизма hA и некоторого слова u \in Σ\ast рассмотрим язык hA1 (u) = { ид G A* | hA(uд) = u };
специально подчеркнем, что этот объект представляет собой множество (а не единственный элемент), причем, возможно, \varnothing. Такую же конструкцию можно рассмотреть для некоторого языка (вместо слова u; пусть это язык B), нас будут интересовать только конечные языки. А именно, hA1(B) = J hA1(u).
u \in B
Теперь рассмотрим другое определение, практически не связанное с предыдущим. Причем, в отличие от других определений настоящей статьи, алфавит ∆ в нем используется в качестве главного. Множество максимальных префиксных кодов (как множество языков) над этим алфавитом будет обозначаться mp(A).
(Не будем давать подробного определения максимального префиксного кода. Вполне достаточно сказать, что это — код, который является максимальным и префиксным, причем все эти понятия присутствуют в «обычных студенческих курсах», [22] и мн. др. То есть можно сказать, что само название уже содержит определение .)
Множество языков, каждый из которых содержит некоторый максимальный префиксный код в качестве подмножества (возможно, несобственного), будет обозначаться записью mp + (A). Таким образом, mp(A) С mp + (A), и, конечно же, для любого алфавита такое включение является собственным. Мы будем называть каждый из этих языков расширенным максимальным префиксным кодом .
Вернемся к рассмотрению главного алфавита £, а также морфизмов вида h A : A A ^ L * . Пусть у нас будет какой-нибудь язык А д G mp(A); тогда считаем, что выполняется следующее условие: h A (A д ) G mp(A); именно так определяется множество языков mp(A) над алфавитом £. Аналогично, для некоторого языка А д G mp + (A) считаем, что h A (A д ) G mp + (A). Следовательно, выполняются такие альтернативные варианты определений:
-
• mp + (A) — это множество языков, каждый из которых содержит некоторый максимальный префиксный код над ∆ в качестве подмножества;
-
• mp + (A) — это множество языков, каждый из которых является А-морфизмом некоторого языка множества mp + (A); т. е. каждый из таких языков является специальным морфизмом некоторого расширенного максимального префиксного кода.
-
2. Бесконечные итерационные деревья
В этом разделе рассматриваются бесконечные деревья специального вида , возникающие в различных прикладных задачах теории формальных языков. Отличительной особенностью этих деревьев является то, что все их ребра помечены буквами заданного алфавита, вершины разделены на некоторые классы эквивалентности, а бесконечные поддеревья, соответствующие вершинам одного и того же класса, эквивалентны. Число полученных классов эквивалентности обычно (но не всегда) конечно.
Бесконечные итерационные деревья обсуждались в нескольких процитированных выше предыдущих статьях; они, как уже было отмечено, возникают во многих моделях теории формальных языков. Среди очень большого числа возможных примеров отметим так называемые ограниченно-детерминированные функции, которые являются предметом изучения студентов-математиков уже на первом курсе (см. уже процитированный выше учебник [22] и др.); часто это — «первое знакомство» студентов с подобными объектами. Однако, несмотря на это, у автора нет каких-либо ссылок на публикации, где были бы введены обобщающие определения для таких объектов. Мы не будем делать этого и в данной статье (т.е. не будем давать строгих формальных определений), а ограничимся только кратким их описанием.
В предыдущих публикациях (см. [3 –6] и др.) рассматривались несколько вариантов таких бесконечных деревьев — здесь приводится один из этих вариантов, имеющий отношение к предмету статьи, т. е. к специальной гипотезе теории формальных языков и к некоторым различным эквивалентным вариантам ее описания, а также к ее применению. Начинаем изложение с достаточно простого описания — которое легко можно довести до строгого определения; в таком описании определяется бесконечное упорядоченное корневое дерево.
В его простейшем варианте рассматривается бесконечное число вершин, помеченных всеми возможными словами над рассматриваемым алфавитом Σ (т. е. всеми возможными словами множества Σ \ast ); для каждого слова u \in Σ \ast и каждой буквы a \in Σ слово u соединено ребром (иногда обозначаемым a) со словом ua. Ясно, что в этом случае корнем дерева является пустое слово ε, и для каждой из других вершин u возможно представление вида u = va (где u, v \in Σ \ast , a \in Σ), и поэтому для каждого такого u также существует соответствующая дуга из v. Иногда будем рассматривать ориентированное (а не корневое) дерево, понятно, что разницы нет; обычно тип дерева (один из этих двух) выбирается просто в зависимости от того, что будет «более удачно» выглядеть на рисунках.
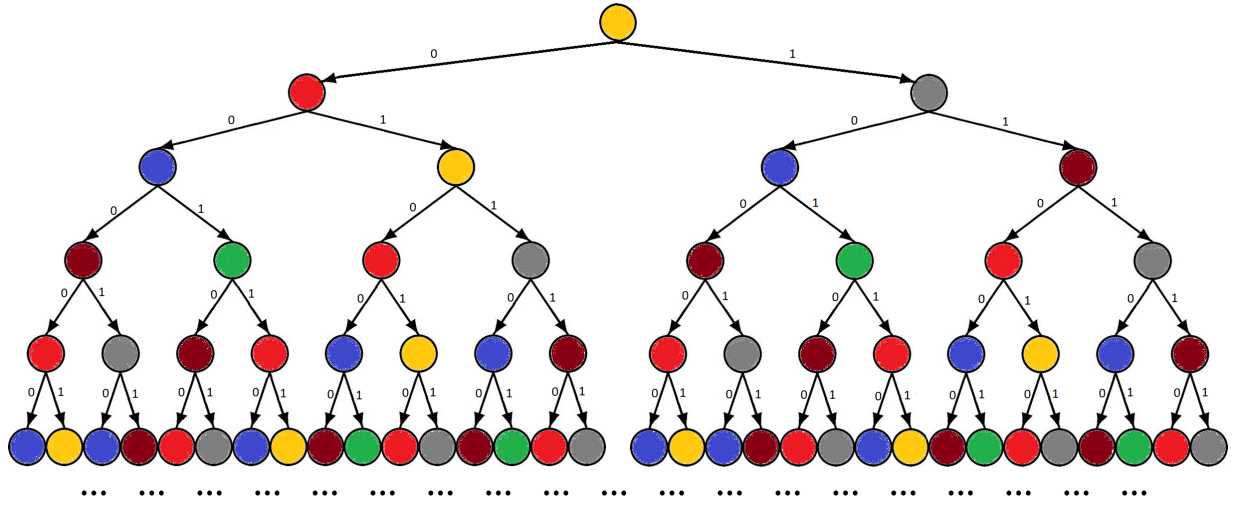
Рис. 1. Пример абстрактного бесконечного итерационного дерева морфизма для алфавита А = { 0,1 } (показаны уровни от 0-го до 5-го)
Однако из всего сформулированного выше еще нельзя получить полное определение бесконечного итерационного дерева; для такого полного определения необходимо добавить, что все вершины дерева каким-то образом разделены на некоторые классы эквивалентности, и бесконечные (под)деревья с корнями, принадлежащими одному и тому же классу эквивалентности, эквивалентны. (Эквивалентность (под)деревьев определяется естествен- ным образом.) См. рис. 1, на приведенном на нем примере разными цветами показаны вершины, принадлежащие разным классам эквивалентности. Отметим также, что условие, сформулированное выше в этом абзаце, эквивалентно другому, более простому: достаточно потребовать, чтобы для каждого ребра, принадлежащего одному и тому же классу эквивалентности, и для всех букв a \in Σ ребра, выходящие из этих вершин, также вели к вершинам одного и того же класса эквивалентности (вообще говоря, к вершинам какого-то нового класса).
Заранее отметим, что во всех рассматриваемых примерах количество классов эквивалентности будет конечным. Немного более подробные комментарии по этому поводу будут приведены в следующем разделе. На рис. 1 такие классы эквивалентности расположены более или менее произвольно, хотя важно отметить, что все свойства и условия, сформулированные выше, выполняются.
Далее рассмотрим пример алфавита из 2 букв (будем алфавит обозначать { a, b } вместо приведенного на рисунке { 0,1 } ). Конкретный пример также может быть получен следующим образом (будем условно называть такие деревья деревьями простейшего уровня). Во-первых, начинаем с дерева, уже рассмотренного на рис. 1, у которого, однако, вершины еще не выделены цветами. Для дальнейших построений задаем язык (пусть это A = { a, ab, bb } ), после чего для этого языка среди вершин дерева отмечаем те, которые соответствуют словам языка-итерации A \ast . Более того, на рис. 2 используются следующие цвета для выделения слов:
\bullet красный — для тех слов языка A \ast , для которых — если их представить именно в виде итераций слов языка A, — последним словом может быть a;
\bullet аналогично синий — для возможного последнего слова ab;
\bullet и зеленый — для возможного последнего слова bb.
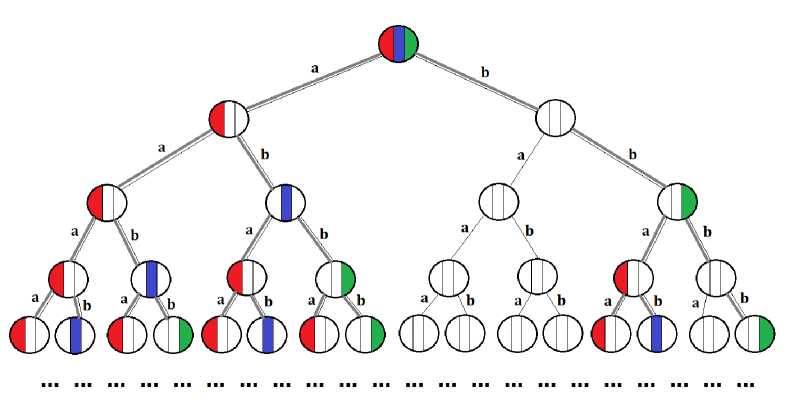
Рис. 2. Пример конкретного бесконечного итерационного дерева морфизма для алфавита £ = {a, b} и языка A = { a, ab, bb } (показаны уровни от 0-го до 4-го)
Отметим, что в нашем примере рассматриваемый язык A является (однозначным) кодом, поэтому все выделенные слова — за исключением пустого слова ε — выделены только одним цветом; однако в общем случае такое выделение одного слова только одним цветом, вообще говоря, необязательно.
Итоговое бесконечное итерационное дерево показано на рис. 2.
Таким образом на дереве отмечены все вершины языка A \ast . Однако, вообще говоря, при таком способе отметки не все вершины бесконечного дерева попадают в множество отмеченных: на рисунке выше они не отмечены ни одним из 3 цветов. Но, несмотря на это, можно считать, что последний факт согласуется с определением бесконечного итерационного дерева; более того, «подгонка» описания определения к набору неотмеченных вершин может быть выполнена любым из рассмотренных далее двух способов. Оба способа проиллюстрированы на рис. 3, обе части рисунка показывают изменения, внесенные в правую часть исходного бесконечного дерева; при этом внесенные изменения выделены фиолетовым цветом.
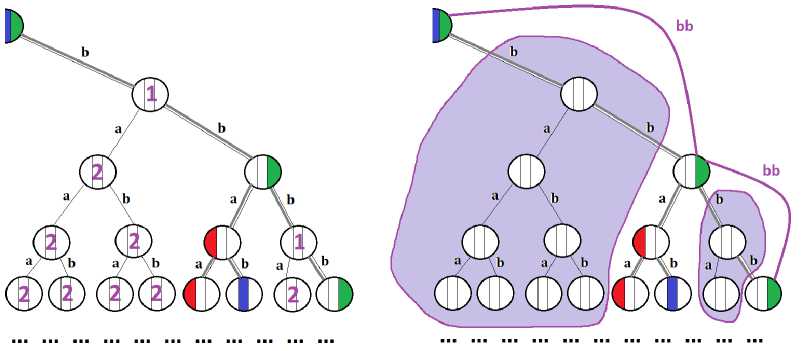
Рис. 3. Два метода, модифицирующих правое поддерево предыдущего дерева. В обоих случаях получается конечное число таких классов эквивалентности
\bullet В первом методе (показанном в левой части рис. 3) мы добавляем новые классы эквивалентности для немаркированных вершин. Названия этих классов отмечены фиолетовыми цифрами 1 и 2. Можно строго доказать, что такое добавление новых классов эквивалентности для немаркированных вершин всегда возможно — после чего получается дерево, полностью удовлетворяющее приведенному выше описанию. Но строгих доказательств приводить не будем: это выходит за рамки настоящей статьи.
\bullet А второй метод состоит:
– во-первых, в том, что разрешается помечать ребра дерева не буквами алфавита Σ, а словами из Σ \ast (при этом уже существующие буквы рассматриваются как соответствующие однобуквенные слова),
– и, во-вторых, в удалении ранее немаркированных вершин дерева и одновременной замене путей, проходящих через них, ребрами, помеченными необходимыми словами (т. е. сочетаниями удаляемых букв).
Такая замена (исключение вершин и старых пометок, а также добавление пометок новых) показана в правой части рис. 3, причем также фиолетовым цветом: удаляемые объекты (вершины и ребра) отмечены фиолетовыми «пятнами» (их показано 2), также легко определить и добавляемые объекты.
Однако для материала настоящей статьи все приведенные варианты бесконечных итерационных деревьев могут рассматриваться только как вспомогательные. Для статьи более важными являются более сложные деревья, построенные в соответствии с несколько более сложным алгоритмом, который в то же время удовлетворяет приведенному выше описанию-определению. В этом разделе такие деревья рассматриваются очень кратко (более подробно — в следующих разделах), однако при этом приводится начало существенно более сложного примера — который будет далее рассматриваться для нескольких разных целей. Для подобных примеров нам нужны два непустых конечных языка (т. е. упорядоченная пара языков) над заданным алфавитом Σ (а не только один язык, как в примерах, рассматривавшихся ранее); в предыдущих публикациях такие два языка почти всегда обозначались как A (первый язык) и B (второй). Вершины такого дерева соответствуют не словам алфавита Σ (в предыдущих примерах ε соответствует слову 0-го уровня, все 1-буквенные слова соответствуют словам 1-го уровня и так далее), а словам нового, специально введенного алфавита ∆; значение этого нового алфавита такое же, как и при введении алфавита того же название «для организации морфизмов». (В нашей ситуации это A-морфизм; его определение см. в разделе 1, а его использование — далее, например в разделе 9.)
При таком способе определения бесконечного дерева предполагается, что пометкой каждой его вершины является подмножество множества префиксов языка B. О методе выбора такой разметки, а также о разметке ребер этого дерева см. ниже. Отметим лишь, что «выходящие» ребра каждого куста дерева желательно обозначать числами от 0 до 3, и эти ребра можно считать соответствующими A-морфизму из алфавита Д = { 0,1,2,3 } в алфавит L = { a, b } .
Итак, в этом разделе приводится только начало примера (см. рис. 4) ; пример полностью (т. е. описание всего бесконечного итерационного дерева, причем не только одно описание, но и подробные варианты применения) будет рассматриваться в дальнейших частях статьи – применительно к нескольким разным дискретным моделям.
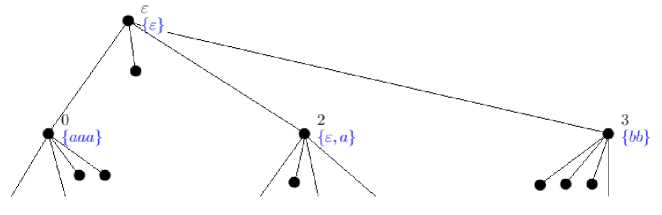
Рис. 4. Начало построения бесконечного итерационного дерева морфизма для пары заданных языков A = { aaa, aabba, abba, bb } и B = { aaaa, abb, abba, bbb }
Как уже было отмечено, само применение бесконечных итерационных деревьев для рассматриваемых в статье задач, а также сведение этих деревьев к конечным автоматам будет рассмотрено в частях II–IV настоящей статьи.
Работа частично поддержана грантом научной программы китайских университетов “Higher Education Stability Support Program” (раздел “Shenzhen 2022 — Science, Technology and Innovation Commission of Shenzhen Municipality”).
Список литературы Об одной гипотезе теории формальных языков. Часть I
- Melnikov B.F., Korabelshchikova S.Yu., Dolgov V.N. On the task of extracting the root from the language // International Journal of Open Information Technologies. 2019. Vol. 7, no. 3. P. 1–6.
- Melnikov B.F., Melnikova A.A. Some more on !-finite automata and !-regular languages. Part I: The main definitions and properties // International Journal of Open Information Technologies. 2020. Vol. 8, no. 8. P. 1–7.
- Мельников Б.Ф., Мельникова А.А. Бесконечные деревья в алгоритме проверки условия эквивалентности итераций конечных языков. Часть I // International Journal of Open Information Technologies. 2021. Vol. 9, no. 4. P. 1–11.
- Мельников Б.Ф., Мельникова А.А. Бесконечные деревья в алгоритме проверки условия эквивалентности итераций конечных языков. Часть II // International Journal of Open Information Technologies. 2021. Vol. 9, no. 5. P. 1–11.
- Мельников Б.Ф. Варианты конечных автоматов, соответствующих бесконечным итерационным деревьям морфизмов. Часть I // International Journal of Open Information Technologies. 2021. Vol. 9, no. 7. P. 5–13.
- Мельников Б.Ф. Варианты конечных автоматов, соответствующих бесконечным итерационным деревьям морфизмов. Часть II // International Journal of Open Information Technologies. 2021. Vol. 9, no. 10. P. 1–8.
- Мельников Б.Ф., Мельникова А.А. Полиномиальный алгоритм построения конечного автомата для проверки равенства бесконечных итераций двух конечных языков // International Journal of Open Information Technologies. 2021. Vol. 9, no. 11. P. 1–10.
- Мельников Б.Ф. Полурешетки подмножеств потенциальных корней в задачах теории формальных языков. Часть I. Извлечение корня из языка // International Journal of Open Information Technologies. 2022. Vol. 10, no. 4. P. 1–9.
- Мельников Б.Ф. Полурешетки подмножеств потенциальных корней в задачах теории формальных языков. Часть II. Построение инверсного морфизма // International Journal of Open Information Technologies. 2022. Vol. 10, no. 5. P. 1–8.
- Мельников Б.Ф. Полурешетки подмножеств потенциальных корней в задачах теории формальных языков. Часть III. Условие существования решетки // International Journal of Open Information Technologies. 2022. Vol. 10, no. 7. P. 1–9.
- Мельников Б.Ф. Лепестковые конечные автоматы: основные определения, примеры и их связь с полными автоматами. Часть I // International Journal of Open Information Technologies. 2022. Vol. 10, no. 9. P. 1–11.
- Мельников Б.Ф. Лепестковые конечные автоматы: основные определения, примеры и их связь с полными автоматами. Часть II // International Journal of Open Information Technologies. 2022. Vol. 10, no. 10. P. 1–10.
- Мельников Б.Ф. Регулярные языки и недетерминированные конечные автоматы (монография). М.: Изд-во Российского государственного социального университета, 2018. 179 с.
- Melnikov B.F. The equality condition for infinite catenations of two sets of finite words // International Journal of of Foundations of Computer Science. 1993. Vol. 4, no. 3. P. 267–273.
- Мельников Б.Ф. Описание специальных подмоноидов глобального надмоноида свободного моноида // Известия высших учебных заведений. Математика. 2004. № 3. С. 46–56.
- Алексеева А.Г., Мельников Б.Ф. Итерации конечных и бесконечных языков и недетерминированные конечные автоматы // Вектор науки Тольяттинского государственного университета. 2011. № 3 (17). С. 30–33.
- Hopcroft R., Motwani R., Ullman J. Introduction to Automata Theory, Languages, and Computation. Massachusetts: Addison-Wesley Publishing Company Reading, 2006. 530 p.
- Hromkoviˇc J. Theoretical Computer Science. Introduction to Automata, Computability, Complexity, Algorithmics, Randomization, Communication, and Cryptography. Berlin: Springer, 2003. 323 p.
- Melnikov B.F. Once more on the edge-minimization of nondeterministic finite automata and the connected problems // Fundamenta Informaticae. 2010. Vol. 104, no. 3. P. 267–283.
- Ахо А., Ульман Дж. Теория синтаксического анализа, перевода и компиляции. Том 1. М.: Мир, 1978. 617 с.
- Melnikov B.F. The complete finite automaton // International Journal of Open Information Technologies. 2017. Vol. 5, no. 10. P. 9–17.
- Яблонский С.В. Введение в дискретную математику. М.: Высшая школа, 2003. 384 с.


