Об одной игровой задаче управления точками вблизи поверхности Луны

Движение материальной точки переменного состава описывается уравнением Мещерского [1]. Управлением является реактивная сила. Если величина тяги задана как функция времени, то управлением является относительная скорость отделяющихся частиц реактивной массы. В этом случае получим задачу об управлении материальной точкой, движущейся под действием заданной по величине силы. В монографии [2] рассмотрена дифференциальная игра преследования «изотропные ракеты». В этой игре преследователь управляет ограниченной по величине силой, приложенной к движущейся материальной точке. Убегающий управляет ограниченной по величине скоростью другой точки. Если допускается мгновенное отделение конечного количества массы топлива с постоянной по величине скоростью, то задача преследования в этом случае сводится к задаче с импульсным управлением [3–6]. В задаче преследования платой [2] является время поимки.

В работе [7] первый игрок управляет реактивной силой точки переменного состава. Величина относительной скорости отделяющихся частиц топлива постоянна, а тяга ограничена заданным числом. Второй игрок управляет ограниченной по величине скоростью второй точки. Решена задача, когда первый игрок стремится сделать в фиксированный момент времени расстояние между точками не меньше заданного числа, расходуя при этом как можно меньше ресурсов.

В настоящей статье рассматривается случай, когда первый игрок, управляя реактивной силой, стремится минимизировать в заданный момент времени расстояние между точками, расходуя при этом как можно меньше ресурсов. Предполагается, что на материальную точку переменного состава, наряду с управляемой реактивной силой, действует постоянная сила, пропорциональная массе точки. Такая ситуация возникает при рассмотрении движения материальной точки вблизи поверхности Луны, где отсутствует атмосферное сопротивление. Сформулированная двухкритериальная задача с помощью весовых коэффициентов сводится к дифференциальной игре, плата в которой является суммой как терминальной, так и интегральной составляющих. Вычислена функция цены игры [2] и найдены оптимальные управления игроков.

Математика

Постановка задачи

Вблизи поверхности Луны точка переменного состава, движение которой описывается уравнением Мещерского

X = ц + d m ⁽ t ) , x _е R n , t <  p , m ( t )

преследует точку, которая движется с ограниченной по величине скоростью y = bv, y е Rn, b > 0, |v| < 1.

Здесь вектор ц е R n определяется постоянной внешней силой, пропорциональной массе точки; величина |^| относительной скорости отделяющихся частиц топлива является постоянной (| • | -норма в R n ); m ( t ) = m 0 + m 1 ( t ) - масса точки, причем m 0 - неизменяемая часть массы, m 1 ( t ) -реактивная масса; p >  0 - заданный момент окончания процесса управления. Считаем, что тяга ограничена числом у >  0

I я—< г . m ( t )

Точкой переменного состава управляет первый игрок. Второй игрок управляет движением второй точки. Цель первого игрока заключается в том, чтобы в момент времени p >  0 сделать расстояние между точками как можно меньше и минимизировать при этом расход топлива. Цель второго игрока – противоположна.

Формализация задачи

Введем новые переменные

.      . .      (p-t)2             я , .      । m(t)1 .

z=y -x-(p -t)x-ц—-—, u = -n, ф(t)=-яv=ту.

2             |я               m (t)

Тогда

| У (p) - x (p )| = |z (p )|, J ф( t) dt = dl ln m’+m^t0).(4)

t0

Здесь m1(t0) – начальный запас реактивной массы. Используя уравнения (1) и (2), получим, что z = -(p -t)ф(t)u + bv; |u| = 1, 0 < ф < y; |v| < 1.(5)

Из формул (4) видно, что сформулированная выше цель первого игрока в переменных (3) p означает, что первый игрок минимизирует |z(p)| и Jф(t)dt. Введем весовой коэффициент а> 0

t ₀

и рассмотрим показатель качества

p

| z ( p )| + a J ф ( t ) dt ^ min max.                                (6)

ф, u v t0

Первый игрок стремится его минимизировать, а второй – максимизировать.

Условия оптимальности в однотипных дифференциальных играх

Рассмотренный пример (5), (6) является частным случаем однотипной дифференциальной игры z = -a(t)ф(t)u + b(t)v, z(10) = z0; 0 < ф(t) < y, |u| = 1, |v| < 1.                  (7)

с критерием качества

p

G (| z ( p )| ) + J g ( t , ф ( t )) dt ^ minmax.                              (8)

ф, u v t0

Здесь a ( t ) >  0, b ( t ) >  0 интегрируемые при t <  p функции. Число y >  0 задано.

Предположение 1 . При каждом ϕ ∈ [0, γ ] функция g ( t , ϕ ) является измеримой по t ∈ ( -∞ , p ] и непрерывна по ϕ при каждом t ≤ p ; 0 ≤ g ( t , ϕ ) ≤ D ( t ) при каждых t ≤ p и ϕ ∈ [0, γ ] , где функция D ( t ) является суммируемой на каждом отрезке [ p ₁, p ] .

Из этого предположения следует, что для каждой измеримой при t ≤ p функции ϕ ( t ) ∈ [0, γ ] сложная функция g ( t , ϕ ( t )) является суммируемой на любом отрезке [ p ₁, p ] [8].

Предположение 2 . Функция G ( ε ) при ε ≥ 0 является непрерывной, строго возрастает и G ( ε ) → +∞ при ε → +∞ .

Рассмотрим оптимизационную задачу

p

G(e) + j g (t, ф(t))dt ^ min,(9)

t ₀

p |z(t0)| + j (b(t) - a(t) ф(t)) dt < e,(10)

t ₀

p max j(b(t) - a(t)ф(t)) dt < e,(11)

t ₀≤ τ ≤ p_τ

ε≥ 0, ϕ: [t0, p] → [0,γ] – измерима.(12)

Теорема 1 [9, теорема 2]. Пусть выполнены предположения 1 и 2, а ε ₀ и ϕ ₀ :[ t ₀, p ] → [0, γ ] – решение задачи (9)–(12). Тогда решением задачи (7) и (8) являются функции ϕ ₀ ( t ) , u ₀ = w ( z ) и v ₀ = w ( z ) , где

w ( z ) = z z при z >  0 и любое w (0) с ограничением w (0) = 1.

Значение цены игры в дифференциальной игре (7) и (8) равна

p

V ⁽ t 0 , z ⁽ t 0 )) = ^e 0 ⁺ j g ⁽ t , Ф 0 ⁽ t )) dt .

t ₀

Теорема 2 [9, теорема 3]. Пусть дополнительно к предположениям 1 и 2 функция g ( t , ϕ ) при каждом t ≤ p является выпуклой по ϕ , а функция G ( ε ) ограничена снизу. Тогда решение в задаче (9)–(12) существует.

Теорема 3 [9, теорема 4]. Пусть выполнено предположение 1, а число ε ₀ ≥ 0 и измеримая функция ϕ ₀ : [ t ₀, p ] → [0, γ ] удовлетворяют неравенствам (10) и (11). Пусть существуют число λ ≥ 0 и неубывающая функция θ :[ t ₀, p ] → R такие, что θ ( t ₀) = 0 и

( p

Я j (b(t) - a(t)Ф0(t)) dt v t 0

-

A

^E 0

= 0,

P j ^( t) (b (t) — a (t Ф (t)) dt = ^( P )E0, t0

G ( ε ₀) - ( λ + θ ( p ) ) ε ₀ ≤ G ( ε ) - ( λ + θ ( p ) ) ε при любом числе ε ≥ 0 ;

g ( t , ϕ ₀( t ) ) - ( λ + θ ( t ) ) a ( t ) ϕ ₀( t ) ≤ g ( t , ϕ ) - ( λ + θ ( t ) ) a ( t ) ϕ , ϕ ∈ [0, γ ], t ₀ ≤ t ≤ p .

Тогда ε ₀ и ϕ ₀( t ) являются решением задачи (9)–(12).

Решение примера

В задаче (5), (6) выполнены равенства

а ( t ) = p - t , b ( t ) = b , G ( ε ) = ε , g ( t , φ ) = αφ .

Поэтому условия (10), (11) и (15)–(18) примут следующий вид: ^p

j(b-(P-t)Ф0(t))dt + |z(t0)|-e0 <0, t0

Математика

	p max J ( b - ( p - 1 ) ф 0( 1 ) ) d1 - £ 0 <  0,		(20)
	t 0≤ τ ≤ pτ । p                                       I
λ	J ( b - ( Р - 1 ф ( 1 ) ) d1 + z ( 1 0 ) - E 0	= 0,	(21)
	к 1 0                                              ) p
	J 0 ( 1 ) ( b - ( p - 1 ф ( 1 ) ) d1 = ^ ( p ) E 0 ,		(22)
	t 0
(1	λ - θ ( p ))( ε 0 - ε ) ≤ 0 при любом	ε ≥ 0,	(23)
( λ + θ ( t ))( p - t ) ) ( ϕ 0( t ) - ϕ ) ≤ 0 при любых ϕ ∈ [0, γ ], t 0 ≤ t ≤ p .			(24)

Из условия (23) получим, что λ = 1 - θ ( p ). Поскольку λ ≥ 0 и θ ( p ) ≥ 0 , то 0 ≤ θ ( p ) ≤ 1 . Подставим это значение λ в формулу (24). Будем иметь

Y при α <θ(t)-θ(p)+1, p-t α ф0(1) = < любое фЕ [0,y] при ----= 0(t)-0(p) +1,                  (25)

P -1

о при ^а- > е (t ) - е (p ) + 1. .            р - ¹

Пусть p -α≤ t0 . Возьмем функции θ(t) = 0 и ϕ0(t) = 0 при всех t0 ≤ t ≤ p . Они удовлетворяют формуле (25). Поскольку λ= 1 -θ( p) = 1 , то из условий (19) и (21) получим равенство

ε ₀ = ( p - t ₀) b + z ( t ₀) .

Максимальное значение по τ в (20) достигается при τ = t ₀ и оно равно ( p - t ₀) b . Поэтому число ε ₀ (26) удовлетворяет условию (20). Условие (22) также выполнено.

В рассматриваемом случае значение цены игры (14) равно V ( t ₀, z ( t ₀) ) = ( p - t ₀) b + z ( t ₀) при t ₀ ≥ p - α .

Пусть

α ≤ и p - ≤ t ₀ <  p - α .                            (27)

γ γ

Возьмем функции θ ( t ) = 0 при t ₀ ≤ t ≤ p ,

ϕ ₀( t ) = γ при t ₀ ≤ t ≤ p - α и ϕ ₀( t ) = 0 при p - α < t ≤ p .               (28)

Они удовлетворяют формуле (25). Из второго неравенства (27) следует, что функция (28) удовлетворяет неравенству b - ( p - t ) ϕ ₀( t ) >  0 при t ₀ ≤ t ≤ p . Поэтому максимальное значение по τ в условии (20) достигается при τ = t ₀ и оно равно

p

J (b - (p - t ф(|( t)) d t0

-

γ

p - t ₀

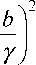
Y I b

+

2 1 Y

a I

+ b α > 0.

Учитывая формулу (29) из условия (21) при λ = 1 , получим, что

Y I              b I Y I b       I о i

^E o =^-™l p ^{- 1} о — I ⁺™l— ^a I ^{+ ва +} z ^{( 1} 0 ) 2 к        Y) 2 к Y )

Очевидно, что условие (20) выполнено.

Из формул (28) и (30) получим, что значение цены игры (14) в рассматриваемом случае равно

V ( t ₀, z ( t ₀)) =- ^γ 2 ( p - t ₀ - α ) ² + ( p - t ₀) b + z ( t ₀) .

Пусть ь           ь           yI        ьI2

a <-, to <  P —, z ( t o) >^ P - t o — L                    (32)

Y         Y         2 V        YJ

Возьмем функцию 6 (t ) = 0 при t ₀ <  t <  p , а функцию ф ₀(t ) определим формулами (28). Как и выше, число £ 0 определяется формулой (30).

Проверим неравенство (20). Имеем p   pp max I ^(t)dt = max (I1,12), 11 = max J ^(t)dt = ab, 12 = max J ^(t)dt, tо  0 при p - b/ Y < t < p . Поэтому в формуле, которая определяет число 12, максимальное значение по т достигается при т = p - b/ Y и

I = ^Y I b - a I + a b .                                   (33)

2 2 V Y J

Стало быть, max ( I 1 , 1 ₂ ) = 1 ₂. Поэтому число £ ₀, определяемое равенством (30), должно удовлетворять неравенству £ ₀ >  1 ₂. Согласно (32) и (33) это неравенство выполнено. В рассматриваемом случае значение цены игры определяется формулой (31).

Пусть

, b               b    । yI a <-, t0 < p —, z(t0) <-|p - t0 — | .

Y         Y 2 V

Покажем, что при некотором числе t ₀ <  q <  p - b/ Y выполнено равенство

Iz(t0)| = f(q), f(q) = yIp-b1 (q-t0)-Y(q2 -t2)•

V ^Y J ²

В самом деле, у квадратного многочлена (35) производная f '( q ) >  0 при 1 ₀ <  q <  p -—.

Y Следовательно, 2

0 = f ( 1 0 ) <  f ( q ) < f I p --I = Y I p - 1 0 --I .

⁰             V Y J 2 V ⁰ Y J

Отсюда и из третьего неравенства в (34) получим существование требуемого числа q .

Возьмем при r = b/ Y функции

	0 при     1 0 <  t <  q ,	Y при 1 0 <  t <  q ,
	a a         _ _       „	b
6 ( t ) =	---при q <  t <  p - r ,    ф 0(t ) =	---- при q <  t <  p - r
	p - t p - q	p - 1
	a	0 при p - r <  t <  p .
	1-- при p - r <  t <  p .
	L p - q

Они удовлетворяют формуле (25). Поскольку число X = a /( p - q ) >  0, то условия (19) и (21)

принимают вид равенства

^£ 0 =^{( b - Y p )( q -} t 0 ^{) +} Y ( q ² - t 0 ) ⁺ — ⁺ | z ⁽ t 0 )1 = —.

2^v Y Y

Здесь использованы соотношения (35).

Далее,

p max I ^(t) dt = max (11,12,13), t0>T

Математика

где p  pp

y (t ) = b ( p - t ) ф ₀( t ), I 1 = max f ^ ( t ) dt , 1 2 = max | ^ ( t ) dt , 1 3 = max [ ^ ( t ) dt .

p - r <т <  p^                  q <т <  p - r^                  t n < т <  q^

T                           T                        т

Подставим сюда функцию ф0(t) (36). Получим 11 = 12 = b2/у. Поскольку ^(t) < 0 при t0 < t< q, то максимальное значение по т при определении числа 13 достигается при т = q. Поэтому 13 = b2/у. Таким образом, max(11,12,13) = b2/у. Отсюда, учитывая формулу (37), получим, что условие (20) выполнено. Подставим функции (36) в условие (22). Получим br = £0.(38)

Числа r = b/у и £ 0 = b ²/ у этому равенству удовлетворяют. Из (36) и (37) следует, что

V(10,z(10)) = £0 + ау\ q-10 + bInp—q I,

I у ^r )

где число q находится из равенства b      I             b 12i q = p 1 I t0- p     I      z(t0) , у К     Y)у а £0 = b2/у и r = b/ у.

Пусть b                           у(        b 12 у(b1

• — < а, t0 < p- a, z(tq) > —I p- t0     I -—I a| .(41)

У                        2 ^       у)   2 ^ у)

Возьмем функцию < 9 ( t ) = 0 при 1 ₀ <  t <  p и функцию ф ₀( t ) из (28). Из условия (21) при X = 1 получим формулу (30).

Поскольку p - а < p - b/ у , то функция (28) удовлетворяет неравенствам b - ( p - 1 ) ф ₀( t ) <  0 при 1 ₀ <  t <  p - а и b - ( p - 1 ) ф ₀ ( t ) >  0 при p - a <  t <  p . Поэтому максимальное значение по т в условии (20) достигается при т = p - а и оно равно b a . Из последнего неравенства в (41)

получим, что число £ ₀ (30) удовлетворяет неравенству £ ₀ > b a . Стало быть, условие (20) выполнено. В рассмотренном случае значение цены игры задается формулой (31).

Пусть b                            1 , xi у( b 1 у( b 1

• - <  ^a , t 0 <  p ^{- a} , z ⁽ t q ) <- I p ^- t 0 — I ^--I— ^a | .                ⁽⁴²⁾

у                        2 ^ у ) 2 ^ у )

Покажем, что существует число 10 < q < p - а, при котором выполнено равенство (35). В самом деле, многочлен f (q) при 10 < q < p - а строго возрастает. Поэтому его максимальное значение на отрезке [10, p - а] достигается при q = p - а и оно равно выражению, стоящему в правой части третьего неравенства в (42). Поскольку f (10) = 0, то требуемое число q существует.

Возьмем функции ^ ( t ) и ф ₀(t ), которые определяются формулами (36) при r = а . Эти функции удовлетворяют формуле (25). Поскольку X = а /( p - q ) >  0, то условия (19) и (21)

принимают вид равенства

^£ о = ( b ^{- p у} )( ^{q -} t 0 ) ⁺ i ^у ( ^{q 2 -} t 02 ) ⁺ Ь ^{а +} | z ⁽ t о)| = b ^a .

Здесь использовано равенство (35).

Функция ф0(t), определяемая формулой (36) при r = а, удовлетворяет неравенствам b - (p -1)ф0 (t) < 0 при 10 < t < p - а и b - (p -1)ф0(t) > 0 при p - а < t < p.

Поэтому максимальное значение в неравенстве (20) достигается при т = p - а и оно равно

( b V у Y( 2

^- у | p ^- у I⁽ q ^- t о ⁾⁺ 2 ( q

— t о ) + b a = -1 z ( t о )| + b a <  £ q

Здесь использовано равенство (35). Числа r = а и £ 0 = b a удовлетворяют равенству (38). Поэтому условие (22) выполнено. Значение цены игры определяется формулами (39), (40) при £ = b a и r = а .

Заключение

С помощью найденной функции ^ ₀( t ) из третьей формулы в (3) вычисляется оптимальный закон расхода топлива. Подставляя в формулу (13) значение z из первой формулы (3), найдем оптимальные направления относительной скорости отделяющихся частиц топлива и скорости второй точки.

Работа выполнена при финансовой поддержке гранта РФФИ в рамках научного проекта № 18-01-00264_a и гранта Фонда перспективных научных исследований ФГБОУ ВО «Челябинский государственный университет» (2018 г.).