Об одной краевой задаче для эллиптического уравнения высокого порядка в многосвязной области на плоскости

2l

X r=0

a    ∂2lu ar ∂x2l-r∂yr

+

X 06r6k62l-1

k aTМ n d U rk   ∂xk-r∂yr

= F

с постоянными старшими коэффициентами a r E R и младшими коэффициентами a rk Е

C ^ (D) краевую задачу

_∂ kj -1 _u

_{∂ n} kj -1

= f i ,

Γ

j = 1,...,1,

где n = n + in2 означает единичную впешшото нормаль и натуральные k j подчинены условию 1 6 k1 < ... < k i 6 21. Как обычно, под порма.тыюй производной (д/ди-У порядка r понимается здесь граничный оператор

∂        ∂r ni^--+ П27Т”

∂x 1      ∂x 2

Аналогичный смысл имеет и граничный оператор (d/de)r по отношению к единичному касательному вектору e = e1 + ie₂ = i(n1 + in₂).

При k j = j имеем задачу Дирихле, а. в случае k j = j + 1. 1 6 j 6 l, эту задачу естественно назвать задачей Неймана, она. была, изучена. А. В. Бицадзе [1] для полигар-монического уравнения. Для однородного уравнения (1) без младших коэффициентов задача. (2) была, рассмотрена, в [2]. Общий случай задачи (1), (2) в классе функций

2 l

2l я r Е C^ (D)

_∂x 2 l - r _∂y r

u Е C²¹ (D) П C^21-1'ДП),  X ar

r =0

был исследован в [3]. В этой работе задача (2) была редуцирована к эквивалентной системе интегральных уравнений в классе C ^(Г) х C ^(D), причем уравнения по контуру были сингулярными. Заметим, что пространство (3) зависит от старших коэффициентов уравнения (1).

В настоящей работе эти результаты распространим на случай обычного пространства C^2l,^(D). В этом случае система интегральных уравнений, о которых шла речь выше, должна рассматриваться в пространстве C ^(Г) х C ^(D), и ее исследование требует отдельного подхода. Ниже все обозначения [3] сохраняются без изменений.

В дальнейшем предполагается, что Г принадлежит классу C^'С В случае l = 1 это условие несколько усилим, потребовав Г G C 1^^+е с некоторым е >  0. Удобно в этой связи под C ¹ л+0 понимать объединение классов C С^^ по в сем е > 0. В частности, Г принадлежит этому классу для всех значений l. Таким образом, функции n1, n₂ и, значит, коэффициенты граничных дифференциальных операторов (2) принадлежат классу C ^21-1,^(Г). Решение уравнения (1) ищется в классе C ^2l,^(D), соответственно его правая часть должна принадлежать C ^(D), а функции fj в краевом условии (2) — классу C ²l-kj +¹,л(Г).

Пусть Vk. 1 6 к 6 m. — все различные корпи характеристического уравнения ао + a1z + ... + a₂iz²¹ = 0 в верхней полуплоскости и lk — кратиость k-го корня, так что Pk lk = l- ^ этими корнями свяжем матрицу B G C^2lxl следующего специального вида.

Если некоторый n-вектор g(z) = (gi(z),.

.,gn(z)) аналитичен в окрестности точек

.

V1, ...,v_m. то. исходя I г;: разбиения l = l1 + ... + lm. можем ввес ми блочную n х l-мат-рипу Wg (v1,...,v_m) = (Wg (v₁),...,W_g(vm)), где матрица Wg(vk ) G C^nxlk составлена, из векторов-столбцов

g^(vk W^(vk ),•••, (l k - 1), g^(lk 1)^(vk).

Применяя это обозначение к 21-стол6цу h(z) = (1,z,..., z^21-1), определим теперь 2l х l- матрипу B равенством B = Wh(v1,..., vm).

Заметим, что квадратная матрица B, составленная из B и B, обратима. Если l х 2l-MaTpiiny. образованную строками обратной матрицы B ^-1. обозиашгть через B 1. то вторые ее l-отрок образуют комплексно сопряженную матрипу. Поэтому B и B¹ связаны соотношением 2 Re BB ¹ = 1, где здесь и ниже 1 означает единичную матрицу (или единичный оператор).

С краевыми условиями (2) свяжем l х 2l-Marpnpy C = (Cjk ) G C ^1,^(Г), элементы которой определяются из соотношений

2l

X Cjk(t)z^k-1 = [ e1(t) + e2(t)z ] ²l kj [ - e2(t) + ex (t)z ] kj 1, 1 6 j 6 l, (4) k=1

где e = e1 + ie2 = i(n1 + m2) — единичный касательный вектор к контуру Г. Заметим, что его направление оставляет область D слева.

Сформулируем аналог основной теоремы из [3] применительно к пространству C^2l,^(D)_ Некоторое отличие состоит только в том. что контур Г в рассматриваемом случае не предполагается простым.

Теорема 1. Пусть контур Г, ограничивающий область D, принадлежит классу C^2l,^ (классу C ^2,^⁺⁰ щ ш l = 1) и состоит из простых контуров Го, Г1,..., Г_п. г тс Го охватывает все остальные контуры.

Тогда в предположении det[C(t)B] = 0, t G Г,

задача (1). (2) фредгольмова в пространстве C2l,^(D) п ее индекс к дается формулой к =--[argdet(CB)]L + l(2l — n),                         (6)

п                     11

где приращение на. контуре берется в положительном направлении (т. е. в направлении, оставляющем область слева) и n есть число связных компонент контура Г.

Заметим, что в случае простого контура (n = 0) эта теорема согласуется с теоремой 1 из [5], полученной по отношению к пространству (3).

C Как II в [3] в принятых прсдположеннях гладкости относительно Г порядки граничных интегральных операторов в (2) можно выровнять (с сохранением эквивалентности задачи).

Условимся для функции у Е C ¹ (Г) под у⁰ понимать производную по параметру длины дуги, отсчитываемой в положительном направлении по отношению к D (т. е. в направлении, оставляющем область D слева). Тогда, очевидно, имеем равенство

(u+)0 = du

∂e

г

здесь и ниже символ ” + ” указывает на граничное значение функции. К сожалению, операция дифференцирования у ^ у0 не является обратимой C 1(Г) ^ C(Г). Однако как показано в [3], этим свойством обладает операция у ^ у0 +

siTy /у(,) d1 t, г

где 5(Г) означает длину контура Г 1i dyt есть элемент длины дуги. Заметим, что r-ая итерация этой операции действует аналогичным образом:

у ^ у⁽ ) ⁺ —[ у^(,) di^,. s^(Г)

г

В соответствии с этим (2) можно заменить эквивалентным краевым условием

dk-1u\(2l kj)     1   f dkj-1u dnkj-1y          5(Г) J dnkj-1

г

di^t = fj²¹ kj ) ⁺ ^ j fj^(,) di^,, ¹ 6 j 6 l. г

Аналогично [3] доказывается, что для u Е C ^2l,^(D) и 2 6 kj 6 2l — 1 справедливо равенство

dkj я/ \⁽²l k^j ) dnkj ^-1

u +   £    bkr

16k+r62l-kj

d^k+r u V ∂x ^k ∂y ^r

с некоторыми -k_r Е C^kj 1’^(Г), которoe при ki = 1 следует заменить на

(u+ )(2l-1)

d²¹ 1u

= de21-1

+ x -зада

1    16k+r62l-2     x a 7

-kr Е C ^(Г).

Во всех случаях краевое условие (7) можно записать в форме

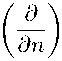
u + £ bkr

d^k+ru V ∂x^k∂y^r

⁺ sTJ

Γ

a kj -1

^"T^di t = j ∂n^{k j 1}

где суммирование ведется по 1 6 k + r 6 2l — 2, коэффициенты b kr E C ^1,^(Г) и fj = ff-kj) +      [ fj (t) dit, k j < 2l.

s(1)

Γ

При j = l и ki = 2l ее следует заменить на fl⁰ = fi. Во всех случаях вектор-функция ^{f 0 e} C ^(г).

Введем блочно-диагональную l х l-матрицу J, составленную из клеток Жордана:

J = diag(Ji,...,Jm),

Jk =

	νk	1
	0	νk
	• 0	• 0
1	0	0

•

•

νk

E Clk^lk

С этой матрицей в дальнейшем связана операция, которая комплексному числу z = x+iy ставит в соответствие l х l-матрицу z j = x + yJ, где x означает скалярную матрицу. В явном виде z j = diag(zji,..., zjm). где

/ x + V k y		y	0 ...	0
	0	x + V k y	y ...	0
z Jk =	• 0	• 0	•                 . . . ... 0 ...	• y
0		0	0 ...	x + V k y /

Обозначим еще через P2 1 -2 класс всех многочленов p(x,y) степени не выше 2l — 2, его размерность, очевидно, дается равенством dim P2 i _-2 = l(2l — 1).

Совершенно аналогично [3] краевая задача (1), (8) редуцируется к эквивалентной задаче для эллиптической системы первого порядка дФ — J^ + M 1ф + M1p = f 1,                     (9)

∂y ∂x

2 Re [(CB)ф⁺] + M ⁰ ф + M⁰p = f ⁰,                      (10)

где оператор M ¹ ограшшеи в C ^(D). onej:>атор M ⁰ компактеп в C ^(Г). а линейные операторы M ¹ 11 M ⁰ действуют соответотвеппо из P2 1 -2 ^ C ^(D) 11 P2 1 -2 ^ C ^1,^(Г) (точное выражение всех этих операторов для дальнейшего несущественно).

Что касается комплексной l-вектор-фупкции f С то она npiшадлежит C ^(D) и определяется равенством f¹ = (B^ 2 i ,..., B/L₁ 2 i , Bj 2 i F ), где B j 2 i представляют собой элементы последнего столбца l х 2l-Marpn^i B ¹, введенной выше. Напомним, что вещественная Свектор-с^уикпия f ⁰ E C ¹ ’^(Г).

Как и в [3] введем интегральные операторы по области:

(11 ^)(z)

= — /^{(t — z)-1} V^(t) d2 t, πi          ^J

D

(S1^)(z)

= — /(t — z)-2^(t) d2t, πi          J

D

z E D, z E D,

где d2t означает элемент площади. Последний интеграл здесь сингулярный и понимается в соответствующем смысле. Необходимое условие существования этого интеграла:

j ^J2 di^ = 0, T где T означает единичную окружность, легко проверяется. Отметим, что в силу четности функции £-2 выполняется и условие j ef die = о,

(ii)

T+

T+

Как показано в [4], для у Е C ^ (D) функция 11^ непрерывно дифференцируема в области D и справедливы формулы

^ = п ^ + sy ^ =

∂x                  ∂y с некоторыми матрицами Пк Е Clxl, связанными соотношением а2 = Ja^. В частности,

∂ ∂y

1 ¹ у = 0.

В силу (11) к сингулярному интегральному оператору S ¹ можно применить теорему 3.5.1 из [5], согласно которой этот оператор ограничен в C ^ (D). С учетом (12) отсюда следует, что оператор 1 ¹ orpaiшчеи C ^ (D) ^ C 1 ’^ (D).

Введем далее интегральные операторы по контуру

⁽¹ 0^^)(z) = 2П /(t - zj¹ dt j Wt).

z ∈ D,

Γ где по отношению к точке t = t1 + it2 на кривой dtj означает комплексный матричный дифференциал dt11 + dt2J и коитур Г ориентирован положителыю по отношению к D. и сингулярный оператор

(S0^)(to) =

— ((t - to)-1 dtj^(t), πi          J t0 Е Г.

Γ

Последний интеграл здесь понимается в смысле главного значения по Коши.

По терминологии [6] функция ф = 1 ⁰ ф является J-аналитичной в области D. т. е.

удовлетворяет уравнению

∂φ _{- J} ∂φ

∂y ∂x

Эта система при J = i переходит в классическую систему Коши — Римана. Как показано в [6], все основные факты теории аналитических функций, связанные с интегральной формулой Коши, распространяются и на решения системы (14).

Очевидно, в случае скалярной матрицы J = i оператор S ⁰ переходит в классический сингулярный оператор Коши, который обозначим через S. Как показано в [7], разность

S⁰ - S является оператором, компактным в С 1^. В [7] также установлено, что в предположении (4) основные результаты классической теории сингулярных операторов [8] распространяются и на оператор

N > = Re [CB(^ + S 0^)],

действующий в пространстве вещественных l-вектор-функций ^ G С ^1,М(Г). Здесь учтено, что в силу принятых предположение относительно гладкости контура Г матрица-функция С (t) в определении (4) прииадлежит классу С 1’^+0 (Г).

Таким образом, этот оператор фредгольмов и его индекс дается формулой ind N0

— — [ arg det(CB)]

Γ

При этом любое решение у G С ^(Г) уравнения Re[CB(^ + S 0^)] = f с правой частью f ^G С ЩГ) ПР1ШМлежит C1»(Г)

Согласно [5] оператор 1 ⁰ ограничен С ¹ ^(Г) ^ С ¹ ’^(D) и справедлива формула Со-хоцкого — Племеля

2(1⁰ ^)⁺ = ^ + S ⁰ ^.                              (17)

Утверждается, что любая функция ф G С1 ’^(D) единственным образом представима в виде ф = 11у1 + 10у0 + i£, £ g Rl                          (18)

с некоторыми комплексной l-вектор-функцией у1 G С^(D) и вещественной функцией у0 G С1 ’^(Г), удовлетворяющей условиям j у (t) d11 = 0,   1 6 j 6 n.

Γj

В самом деле, положим n 1 _(d т9Ад у = Vdy — Jaxp, ii пусть ф0 = ф — 11у1. Тогда в силу (13) функция ф0 являстся J-аналптпческой в области D. т. е. удовлетворяет уравнению (14). и принадлежит классу С1 ’Ц(В). Поэтому дело сводится к представлению ф0 = 10у0 + i£, £ g Rl, с условиями (19) на вещественную плотность у.

В случае пространств С ^ это предложение установлено в [9] (см. также [10]). Таким образом, функция у⁰ является решишем уравнения Re(^ + S 0^) = f с правой частью f = Reф⁰, которая по условию принадлежит классу С ¹ ’^(Г). Как отмечено выше, в этом случае его решение у⁰ также npiшадлежит С ¹ ’^(Г).

Пользуясь представлением (18) и формулой Сохоцкого — Племеля (17), задачу (9), (10) можем эквивалентным образом редуцировать к системе относительно набора (у1, у0, р, £), которая определяется уравнениями у1 + M1 (11у1 + 10у0 + i£) + М^р = f 1,

2Re [СВ(11у1)+ + i£] + Re СВ (у0 + S0у0) + М 0(11 у1 + 10у0 + i£) + f0 р = f0, подчиненной условиям (19). Введем для краткости пространство X = P2/-2 х Rl, которое согласно (8) имеет размерность dimX = 1(21 - 1) + 1 = 212,                             (20)

операторы

N ¹¹ = у¹ + M 111у1, N ¹⁰ = M 11 0,

N01^1 = 2 Re [CB (IV )^+] + M011у1,                    (21)

N⁰⁰ у⁰ = Re [CB(y⁰ + S ⁰у)] + M⁰I⁰у⁰ , и, наконец, операторы

T Чр^) = M1P + 1 0 (O, T0(p,0 = M0P - 2Im(B)£ + M ⁰(i£).

Тогда предыдущую систему можем записать в краткой форме

N (у1 ,у0) + T (p,<) = (f 1,f 0)(22)

с операторными матрицами

11      101

N = N 01 N 00   , T =   T 0•

Согласно (20) пространство C^(D) х C 1,^(Г) х X является расширением пространства C^(D) х C 1,М(Г) на 212 измерений, поэтому на основании известных свойств фредгольмовых оператров [11] операторы (N, T) и N фредгольмово эквивалентны и их индексы связаны соотношением ind(N, T) = ind N + 212.                             (23)

С другой стороны, условие (19) выделяет в пространстве C 1,М(Г) замкнутое подпространство коразмерности ln, поэтому из тех же соображений индекс к системы (22), (19) связан с индексом оператора N соотношением к = ind(N, T) - ln.                              (24)

Рассмотрим подробнее операторы (21). Условимся писать N1 ~ N2, если разность N1 — N2 является компактным оператором. Вспоминая, что оператор оператор M ⁰ компактен в C 1'^(Г), в обозначениях (15) можем написать

N ¹¹ ~ 1, N ¹⁰ ~ 0, N ⁰⁰ ~ N ⁰

и, следовательно,

N ~ M = ( Nt №0 ) •                     (25)

Как отмечено выше, оператор N ⁰ фредгольмов и его индекс дается формулой (16). В частности, существует его регуляризатор, т. е. ограниченный в C 1 '^ оператор R со свойством R°N ⁰ ~ N0R⁰ ~ 1. Непосредственно проверяется, что оператор

MM

Но тогда на основании (25) N — фредгольмов оператор, а вместе с ним и исходная задача (1), (2).

Пусть M(t) 0 6 t 6 1. получает*-я 'заменой N ⁰¹ на tN ⁰¹ в определении (25) оператора M. Те же соображения показывают, что оператор M (t) также (фредгольмов. Поскольку он непрерывно зависит от t, его индекс не зависит от t и, в частности, ind M = ind M (0) = ind N 0. В сил у (25) ind N = ind N 0. что вместе с (16) ii (23). (24) завершает доказательство формулы индекса (6) и теоремы. B