Об одной линейной задаче управления при наличии помехи
Бесплатный доступ
Рассматривается линейная задача управления при наличии воздействия со стороны неконтролируемой помехи. Её значения принадлежат компакту. Управление ищется в виде произведения скалярной функции на векторную функцию. Терминальная часть платы зависит от модуля линейной функции вектора состояния. Интегральная составляющая платы является интегралом на отрезке от степени скалярной функции. Найдены необходимые и достаточные условия, при выполнении которых допустимое управление является оптимальным.
Управление, помеха, дифференциальная игра
Короткий адрес: https://sciup.org/147158937
IDR: 147158937 | DOI: 10.14529/mmph170205
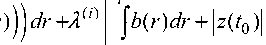
Список литературы Об одной линейной задаче управления при наличии помехи
- Красовский, Н.Н. Позиционные дифференциальные игры/Н.Н. Красовский, А.И. Субботин. -М.: Наука, 1974. -456 с.
- Айзекс, Р. Дифференциальные игры/Р. Айзекс. -М.: Мир, 1967. -479 с.
- Понтрягин, Л.С. Линейные дифференциальные игры преследования/Л.С. Понтрягин//Мат. сб. Новая серия. -1980. -Т. 112, № 3. -C. 307-330.
- Ухоботов, В.И. Метод одномерного проектирования в линейных дифференциаль¬ных играх с интегральными ограничениями: учебное пособие/В.И. Ухоботов. -Челябинск: Челяб. гос. ун-т. -2005. -124 с.
- Ухоботов, В.И. Однотипные дифференциальные игры с выпуклой целью/В.И. Ухоботов//Тр. ИММ УрО РАН. -2010. -Т. 16, № 5. -C.196-204.
- Ухоботов, В.И. Однотипные дифференциальные игры с выпуклой интегральной платой/В.И. Ухоботов, Д.В. Гущин//Тр. ИММ УрО РАН. -2011. -Т. 17, № 1. -C. 251-258.
- Красовский, Н.Н. Теория управления движением/Н.Н. Красовский. -М.: Наука, 1968. -475 с.
- Колмогоров, А.Н. Элементы теории функций и функционального анализа/А.Н. Колмогоров, С.В. Фомин. -М.: Наука, 1972. -496 с.
- Кудрявцев, Л.Д. Курс математического анализа. T.1./Л.Д. Кудрявцев. -М.: Высшая школа, 1981. -687 с.
- Пшеничный, Б.Н. Выпуклый анализ и экстремальные задачи/Б.Н. Пшеничный. -М.: Наука, 1980. -319 с.
- Люстерник, Л.А. Элементы функционального анализа/Л.А. Люстерник, В.И. Соболев. -М.: Наука, 1965. -520 с.
- Рисс, Ф. Лекции по функциональному анализу/Ф. Рисс, Б. Секельфальви-Надь. -М.: Наука, 1979. -587 с.
- Иоффе, А.Д. Теория экстремальных задач/А.Д. Иоффе, В.М. Тихомиров. -М.: Наука, 1974. -479 с.
Статья научная
