Об одной математической модели изгибаний поверхности

Исследуемая математическая модель бесконечно малых изгибаний поверхности положительной кривизны [1] сводится к задаче Римана-Гильберта с разрывными краевыми условиями для системы уравнений Коши-Римана. Несмотря на достаточно глубокое изучение этой проблемы в монографии [1], интересным остается довольно большой круг вопросов, связанных с конкретными поверхностями и условиями на границе поверхностей. В данной статье для поверхностей положительной гауссовой кривизны находится поле смещений при бесконечно малых изгибаниях без сжатия, если условия на границе поверхностей приводят к задаче Римана-Гильберта с разрывными краевыми условиями. Аналитическое и численное исследования проводятся методами, разработанными в статьях авторов [2, 4].

Математическая модель бесконечно малых изгибаний поверхностей положительной кривизны

Пусть r = r (tx, t2)— кусочно-гладкая поверхность S c R3 с уравнением r = r (t1, t2 ) = r (t1, t2 ) + 8 p (t1, t2 ), где 8— числовой параметр, p(tx, t2 )g C 1(S), задано семейство поверхностей Ss в R3.

Если ds 2-ds2 =O (s2), то говорят, что поверхности S являются бесконечно малыми изгибаниями поверхности S [1].

Получим дифференциальные уравнения этих изгибаний:

ds ² = ( dr , dr ),   ds 2 = ( dr. , dr_e ) = ( dr +8 dp , dr +8 dp ) = ( dr , dr ) + 2f( dr , dp ) +

+ 8 ² ( dp , dp ), ds_E ² - ds² = 2e ( dr , dp ) + e² ( dp , dp ).

Отсюда для того чтобы поверхность S была бесконечно малым изгибанием поверхности S необходимо и достаточно выполнение условия

( dr , dp ) = 0.                                                (1)

Это векторное уравнение бесконечно малых изгибаний поверхности S .

Если r = (x, y, z), p = (^ту,^), то уравнение (1) запишется в виде dxd£ + dydp + dzd^ = 0.                                (2)

Пусть поверхность S задана явным уравнением z = f (x, y), функция f (x, y) рассматривается в области D, которая является проекцией поверхности S на координатную плоскость xOy . В этом случае dz = zxdx + zydy, d^ = ^ Xdx + ^ ydy,  dp = pxdx + pydy,  d^ = (^xdx + ^ydy.

Подставляя эти выражения в (2), получаем уравнение

(£x + zx^x ) dx2 + (^y +r!x+ zx^y + zy^x ) dxdy + (77y + z^y ) = 0, откуда следует fx + ZxC = 0, e, + n, + z£, + zx, = 0, n, + z,<, = 0.

Подстановка u, = 2; + zx^, иг=р + z ^ приводит к системе уравнений и 1 x-zxx^ = 0,  “ 1 y+u2x -2zxy^ = 0,  “2y-zyy^ = 0.

После исключения переменной получаем систему уравнений в матричной форме где

A

zyy

- 2 z

xy

AU x

BU, =0,

z

0 >

B

z

zxx

, U =

“ 1

u

.

Для системы уравнений (3) условие z z —z1 >0 xx yy      xy обеспечивает ее эллиптичность в области D . Гауссова кривизна поверхности S задается формулой xx yy      xy

, (1 + z x ² + z 2 )²

поэтому система уравнений (3) будет эллиптической тогда и только тогда, когда поверхность S имеет положительную гауссову кривизну. После ряда неособых преобразований система (3) приводится к обобщенной системе уравнений Коши-Римана.

Бесконечно малые изгибания эллиптического параболоида

Пусть S – некоторая часть эллиптического параболоида z = Px ^Q2 Qxy + Ry ², PR-Q ²>0.

Найдем нетривиальное поле смещений при бесконечно малых изгибаниях этой поверхности. Сначала рассмотрим простейший случай z = x ² + y ². Так как z_xx = z^ =2, z^ = 0, то система уравнений (3) сразу становится системой Коши-Римана

AUx + BUy =0,                                    (4)

где

10)     <0 -1)

, в

⁰ 1)      U ⁰J

Отсечем

от кругового параболоида z = x ² + y²

его

часть

S плоскостями

x = 0, x = k, y = 0, y = l. Нормальный вектор параболоида в любой точке имеет вид n = (-2x, -2y, 1). Пусть на границе прямоугольника D, ограниченного линиями пересечения координатной плоскости xOy с указанными выше плоскостями, выполнены условия

U (x, 0) = u (k, y) = u2 (0, y) = u2 (x, l) = 0.(5)

Доказано [2], что для системы уравнений

AUx+BUy+C (x, y )U = F ( x, y ), при достаточной малости матрицы C(x, y), а именно при выполнении неравенства

IIСиL5“UIL, 0',2\'l:,

(здесь ||‘|| - норма в пространстве L2 (D)) для VF(x, y)е L2 (D) существует единственное решение U(x, y)е W1(D), удовлетворяющее условиям (5) (задача Римана-Гильберта с раз- рывными краевыми условиями), причем имеет место неравенство IIUL ^mFL, m=const.

Поэтому задача (4), (5) имеет в прямоугольнике D единственное тривиальное решение

Г 0

< 0

U ( x , y )

, т.е. £ = -2 x <, p = -2 y <.

Следовательно, поверхность S подвержена бесконечно малым изгибаниям, определяемым вектором p ( x , y ) = -2 x ,-2 y ,1 (xx, y ), где (( x , y )- произвольная, достаточно гладкая функция, заданная в области D .

Полученное выражение для p ( x , y ) показывает, что нетривиальный вектор смещения в каждой точке поверхности коллинеарен нормальному вектору этой поверхности.

В общем случае уравнение эллиптического параболоида z = Px2 + 2Qxy + Ry2

заменой z = Pz, x' = P|x + Qy |, y1 = pRR - Q2 y сводится к уравнению z' = x'2 +y'2.За- данная этим уравнением поверхность S , расположенная над прямоугольником D = {( x', y) 10 < x kk, 0 < y < l}, имеет бесконечно малые изгибания, определяемые вектором смещения p'(x',y ) = (-2x',-2.y’,!XXx',y') • При указанной выше замене переменных прямоугольник D преобразуется в параллелограмм D , ограниченный прямыми y = 0, y =

l

P

Pk

I        , y =--x , y =--x + — ,

PRrQq*     q     q q

поверхность S'— в поверхность S , заданную

общим уравнением параболоида в параллелограмме D . Поэтому поверхность S имеет бесконечно малые изгибания, определяемые вектором смещения, который задается формулой 2x1

U ( x , y ) = (-2 Px - 2 Qy ; - 2^/ PR -Q ; 1) x, y), где ^(x, y) - произвольная функция.

Дальнейшие исследования задачи Римана-Гильберта для обобщенной системы Коши-Римана показали, что область D может быть выбрана произвольной, имеющей достаточно гладкую границу. В работе [3] доказано, что для системы уравнений (6), при выполнении условия (7) однозначно разрешима в пространстве W1 (D) задача с краевыми условиями м11г-иг°=0’   u 2I1'    °'

где п = ( n , n ₂)- единичный вектор внешней нормали к границе Г , а сама граница разбита на части следующим образом:

I    {( x , у )еГ: П 1> 0}, Г" = {( x , у )еГ: П 1 с 0},  Г⁰=Г\( РцЕ).

Следовательно, выводы о бесконечно малых изгибаниях параболоида остаются в силе для его части S с достаточно гладкой границей.

Численный анализ математической модели бесконечно малых изгибаний эллиптического параболоида

Разрешимость задачи (4), (5) для произвольной вектор-функции F ( x , у )е L ₂ ( D ) позволяет утверждать однозначную разрешимость следующей задачи.

Задача. В единичном квадрате D= (x, у ):0< x <1; 0< у <1 найти решение системы уравнений (4) при выполнении краевых условий u11у=0 = ^1 (x),   u1 lx= 0 = ^2 (у ),   u2 | у=1 = ^1 (x),   u2 |x=1 = ^2 (у ) .                  (8)

Функции в краевых условиях можно взять, например, из класса непрерывных функций. Тогда простой заменой неизвестных функций задача (4), (8) сводится к задаче с нулевыми граничными условиями для неоднородной системы Коши-Римана.

Перейдем к построению численного алгоритма решения задачи (4), (8). Известно, что система уравнений (1) является условием аналитичности функции комплексной переменной w(z ) = u ( x , у ) + iu ₂ ( x , у ), z = x + iy , что, в свою очередь, влечет бесконечную дифференцируемость в области D функций u ( x , у ) и u ₂ ( x , у ). Поэтому процесс численного решения задачи можно упростить [4].

Из постановки задачи следует, что функция u ( x , у ) является решением следующей задачи

А ^U , ^u , xx+^U 1 уу =⁰ , ^{(9) U} J _{у =0} = ^^{( x} ); ^u J _{x =0} = ^( у ); ^u 1 у ^ ^{= <9}1⁽ x ); ^u 1 x l _{x =1}=^ ( у ) , ⁽¹⁰⁾

где из условий (8) ^( x ) = -^( x ),  ^₂( у ) = у^( у ) •

Таким образом, для нахождения функции u ( x , у ) имеем третью краевую задачу для уравнения Лапласа.

Для решения задачи (9), (10) в квадрате D берем сетку ij i, j= qq

, i , j = 0, q ,   h = ¹,

q

на которой вводим разностные отношения [5, 6] (индекс у функции опускаем)

u xx [ i , j ] - 4( u [ i -1, j ] - 2 u [ i , j ] + u [ i + 1, j ]),    U yy [ i , j ] - -12( u [ i , j -1] - 2 u [ i , j ] + u [ i , j + 1]).

hh

В результате для решения поставленной задачи (9)/ (10) получаем разностную схему

	u [ i , j -1] + U [ i -1, j ] - 4 u [ i , j ] + u [ i +1, j ] + u [ i , j +1] = 0, i , j = 1, q -1 u [ i ,0] = ,1[ i ],    i = 0, q u [0, j ] = ^2[ j ],   j = 0, q
	u [ i , q -1]- u [ i , q ] = — 0x] i ], i = 1, q q u[q ~ 1 j ] - u [ q , j ] = -16>2[ j ],   j =1, q q (p 1 [0] = ^[0]-

Для вычисления значений функции u^ (x, у) на той же сетке вводим разностные отношения u x[i,j>7 uji + 1,j]-uji,j] ,  u у[i,j 1*7 u^i,j + 1]-U1[i,j] ;

hh u 2 x [ i, j]'~7 u 2[ i -1> j]- u 2[ i, j] ,  u 2 у [ i, j^“T u 2[ i, j ”1] -u 2[ i, j]

hh и из самой системы (4) получаем разностную схему

-2u 2 [ i , j ] + u 2 [ i +1, j ] + u 2 [ i , j + 1] = u 1 [ i +1, j ] u [ i , j +1],   i , j = 0, q “1

• u , [ i , 0] = ^ [ i ],   i = 0, q

• < U 1 ^[°, j MaI j ^],   j = ^0, q

u^[i, q]= У\[i], i= °, q u2[q,j] = ^[j],  j = 0, q ф1[0] = ^[°],  ^1[q] = ^[q] .

Для численной реализации этих двух разностных схем разработана программа на языке «Turbo Pascal» [7]. (При необходимости авторы могут выслать листинг программы по электронной почте).

Для контрольного примера u (x, у) = 2xy,  v(x, у) = у2 - x2 при q = 10 программа выда- ет следующие результаты:

Матрица значений u ( x , у )

0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,00 0,02 0,04 0,06 0,08 0,10 0,12 0,14 0,16 0,18 0,20 0,00 0,04 0,08 0,12 0,16 0,20 0,24 0,28 0,32 0,36 0,40 0,00 0,06 0,12 0,18 0,24 0,30 0,36 0,42 0,48 0,54 0,60 0,00 0,08 0,16 0,24 0,32 0,40 0,48 0,56 0,64 0,72 0,80 0,00 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00 0,00 0,12 0,24 0,36 0,48 0,60 0,72 0,84 0,96 1,08 1,20 0,00 0,14 0,28 0,42 0,56 0,70 0,84 0,98 1,12 1,26 1,40 0,00 0,16 0,32 0,48 0,64 0,80 0,96 1,12 1,28 1,44 1,60 0,00 0,18 0,36 0,54 0,72 0,90 1,08 1,26 1,44 1,62 1,80 0,00 0,20 0,40 0,60 0,80 1,00 1,20 1,40 1,60 1,80 2,00

Матрица значений u ₂ ( x , у )

0,00 -0,01 -0,04 -0,09 -0,16 -0,25 -0,36 -0,49 -0,64 -0,81 -1,00 0,01 -0,00 -0,03 -0,08 -0,15 -0,24 -0,35 -0,48 -0,63 -0,80 -0,99 0,04 0,03 -0,00 -0,05 -0,12 -0,21 -0,32 -0,45 -0,60 -0,77 -0,96

0,09 0,08 0,05 -0,00 -0,07 0,16 0,15 0,12 0,07 -0,00 0,25 0,24 0,21 0,16 0,09 0,36 0,35 0,32 0,27 0,20 0,49 0,48 0,45 0,40 0,33

0,64 0,63 0,60 0,55 0,48 0,81 0,80 0,77 0,72 0,65 1,00 0,99 0,96 0,91 0,84

-0,16 -0,09 -0,00 0,11 0,24 0,39 0,56 0,75

-0,27 -0,40 -0,55 -0,72 -0,91

-0,20 -0,33 -0,48 -0,65 -0,84 -0,11 -0,24 -0,39 -0,56 -0,75 -0,00 -0,13 -0,28 -0,45 -0,64 0,13 -0,00 -0,15 -0,32 -0,51 0,28 0,15 -0,00 -0,17 -0,36 0,45 0,32 0,17 0,00 -0,19 0,64 0,51 0,36 0,19 0,00

Оба знака после запятой в этих таблицах точные.

При изменении краевых условий (их значений в узлах, которые попали на границу квадрата) на величину е = 0,1 значения решений во всех узлах изменяются на эту же величину, т.е. | и_х uu_Xe |=| u₂ - v_2Е |= 0,1. Этот результат свидетельствует об устойчивости как самой задачи, так и численного алгоритма.

Графики функций приведены ниже.

2,5

1,5

0,5

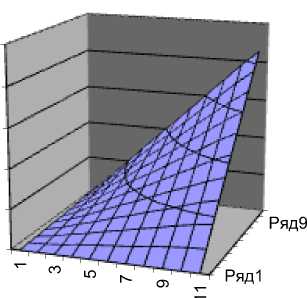
Рис. 1. График функции и_х ( x , у)

2,5

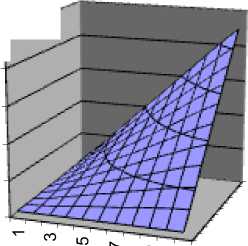
Ряд10

Ряд1

Рис. 2. График смещенной функции и_х Д x , у )

1 0,8 0,6 0,4 0,2

0 -0,2 -0,4 -0,6 -0,8

-1

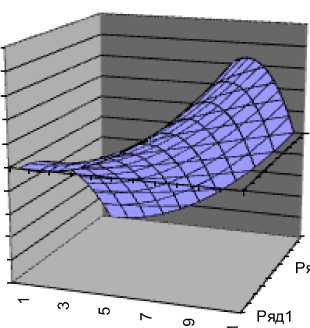
Ряд1

Рис. 3. График функции u₂ ( x , у )

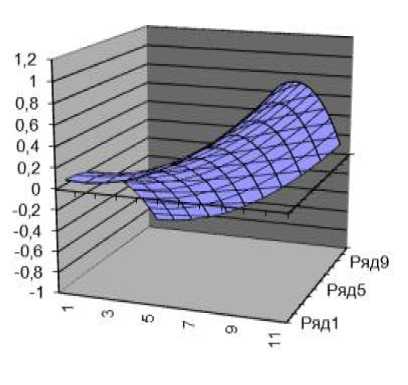
Рис. 4. График смещенной функции u ₂Д x, у )

Заключение

Проведенное аналитическое и численное исследование математической модели бесконечно малых изгибаний эллиптического параболоида как в частном случае, так и в общем позволяют найти поле смещений для произвольных частей этого параболоида, если эмпирическим или теоретическим путем найдены смещения на границе кусков поверхности. Полученные результаты могут быть использованы в геометрии поверхностей и в механике.