Об одной многоточечной краевой задаче для дифференциального уравнения второго порядка

Рассмотрим краевую задачу

x‘(t) = f (t, x(t), x'(t)) + h(t) ,      (1)

x ⁽⁰⁾ = ^{x ( £ )}, x ( 7 ) = x ⁽¹⁾ ,     (2)

где      t е [ 0,1 ]        £ , пе (0;1),     функция

, f :[0,1] x R1 x R1 ^ R1 удовлетворяет условиям Каратеодори.

В предлагаемой работе исследуется случай, когда £ + ц = 1, причем безотносительно взаимного расположения значений £ и п на интервале (0;1). В частном случае, ко

Введем основные обозначения.

Пусть L p = L p [ 0;1 ] – пространство суммируемых по Лебегу в p -й степени функций l                        ¹ p

x :[0;1] ^ R , с

нормой 1 x 1^ = j | x l⁽ s ) p ds

У 0

;

L _да [0;1] - пространство ограниченных в существенном функций x :[0;1] ^ R , с нормой

||x ||_£ = vrai sup x ( t )| ;    D_p = D_p [ 0;1 ]

–

да да

t g [0,1]

про-

гда £ = п = “ , задача (1), (2) принимает вид трехточечной задачи для уравнения второго порядка. Отметим, что такая задача находит широкое применение в различных областях теории управления, экономике и т.д., поэтому изучалась многими авторами (см., например, [1, 2]).

странство абсолютно непрерывных функций x : [0;1] ^ R , таких, что x е L_p , с нормой II x I D = x ⁽⁰⁾l⁺1I x l l _p • Через W p = W p ^[ 0;^{1 ]} , 1 <  p < да обозначим пространство абсолютно непрерывных вместе с первой производной функций x :[0,1] ^ R , таких, что x 'е D_p x " е L_p , с нормой

II ^x L = l ^{x (0)}l ⁺ x '⁽⁰⁾1+1 l x¹

Wp

."

Lp

.

Всюду далее q - сопряженный с p показатель

11,,

—I— = 1, 1 <  p < ^ .

pq

Определение 1. Под решением задачи (1), (2) будем понимать такую функцию x е W_p [ 0;1 ] , удовлетворяющую почти всюду на отрезке [ 0;1 ] уравнению (1) и условиям (2).

Сформулируем условия разрешимости задачи (1), (2) в виде теоремы.

Теорема 1. Пусть выполнены следую- щие условия:

• 1)    существуют неотрицательные постоянные a, b и неотрицательная функция g е L _и [ 0;1 ] , такие, что

• |f(t, u1, u2 ) ^ au11 + bu21 + g(t)

при u 1 , u ₂ е R ¹ и почти всех t е [ 0;1 ] ;

• 2)    существует u * > 0 , такое, что sig^ ) f(t , U 1 , u 2 ) -| \h^_L >  0 (или sigdu ) f ( t , u 1 , u ₂ ) +| \h\_L <  0) при j u j >  u* и

• почти всех t е [0;1] и для всех u 2 е R1;

• 3)    справедливо неравенство

  ( a + b

  
  
  

^

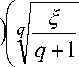
+ 1 <  1.

)

Тогда задача (1), (2) имеет хотя бы одно решение в пространстве W_p .

Прежде чем перейти к доказательству теоремы, приведем необходимые утверждения и определения.

Вместе с задачей (1), (2) рассмотрим соответствующую линейную задачу:

x "(t) = h (t) x(0) = x(^), x(n) = x(1) .

Подпространство решений этой задачи определим равенством

W p [ 0,1 ] = { x е W p [ 0,1 ]| x (0) = x (&, x ( n ) = x (1) } с нормой пространства W _p .

На этом пространстве задачу (1), (2) представим в виде операторного уравнения

Lx = Fx ,            (3)

где операторы L , F : W p ^ L_p определяются следующим образом:

(Lx )(t ) = x "(t), (Fx )(t ) = f (t, x, x') + h (t).

Таким образом, для доказательства разрешимости задачи (1), (2) достаточно исследовать на разрешимость операторное уравнение (3). Оператор L в уравнении (3) оказывается необратимым (см. ниже), следовательно, по терминологии, принятой для квазилинейных операторных уравнений, задача (3) называется резонансной .

Для линейного оператора L : X ^ Y , где X , Y - банаховы пространства, через ker L и imL соответственно обозначим ядро и образ оператора.

Нам потребуется понятие обобщенно обратного к оператору L оператора. Пусть P : X ^ X - проектор на ядро оператора L и P C = I - P - дополнительный проектор [3]. Так как понятие обобщенно обратного оператора трактуется по-разному, в работе мы будем следовать определению, сформулированному в [4].

Через K_p : imL ^ X обозначим обобщенно обратный к оператору L : X ^ Y , ассоциированному с проектором Р [4]. Напомним, что для оператора K _p справедливы условия:

• 1)    LK_p = 1 ₀ , где I _o: imL ^ Y - оператор естественного вложения;

• 2)    K_pL = P c ;

• 3)    P c K p = K p .

Для непрерывного оператора F : X ^ Y определим неотрицательную числовую характеристику равенством:

ь ( f ) = im F Y <® ,

• ^{11 x|}X     M x

называемую квазинормой оператора F . Если Ь ( F ) <+® , то оператор F принято называть квазиограниченным [ААР]. Если F = T - линейный оператор, то b ( F ) совпадает с нормой оператора T , т.е.     Ь ( F ) = | Т | |. Если

||Fx | ^ A + B||x||³ , то Ь ( F ) = 0 при 0 <  3 <  1 и Ь ( F ) <  B при 3 = 1.

Для определения условий разрешимости уравнения (3) воспользуемся вспомогательным утверждением о разрешимости операторных уравнений. Воспользуемся теоремой, приведенной в работе [5].

Пусть X = ker L © X_o - разложение в прямую сумму замкнутых подпространств.

Теорема 2 . Пусть выполнены условия:

• 1)    L – нетеров;

• 2)    F – вполне непрерывен;

• 3)    существуют такие числа у , 3 >  0 , что для каждого элемента х₀ е Х _о существует элемент и е ker L такой, удовлетворяющий требованиям F ( х ₀ + и ) е imL , || u || <  у\\х ₀|| + 3 ;

• 4)    b ( F )(1 + у ) <| K p ||.

Тогда уравнение (3) имеет хотя бы одно решение.

Для      оператора       L : X ^ Y ,

( Lx )( - ) = х " (t ) ядро и образ определяются равенствами:

ker L = {х е W, | х = c, c е R},

£ s+п imL = {у е L | — j | у(т)dTds = 0}.

p £ 0

Представим Wp0 в виде разложения в прямую сумму подпространств ker L © Xо и для произвольного х е W,   полагаем х = и + хо, где и е kerL, хо е Xо. В качестве проектора P рассмотрим оператор P: W ^ W,      (Рх \t) = х(0),     через

Q : L_p ^ L_p обозначим проектор на образ оператора L .

Лемма 2. Обобщенно обратный оператор для оператора L , ассоциированный с проектором P , имеет следующий вид:

t £ s                  t s

кру = —jj у (т) dтds + j J у (т)drds, у е imL .(4) p    £00         00

Норма оператора Kp  удовлетворяет оценке

K p y_Wp

(         Л

< q - ^£ - + 1 • у . Ц| q + 1 J ¹¹ " p

Доказательство. Проверим выполнение свойств обобщенного обратного оператора:

£ s

ts

''

Лемма 1. Оператор, определенный равенством

£ s +п

(Qy)(-) = у(t)- 1г j | у(т)dтds ,

0 s

является проектором на образ оператора L _.

Доказательство. Рассмотрим оператор Q^c = I - Q и проверим, что он является проектором, такой оператор называется дополнительным проектором к проектору Q .

Действительно,

£ s + 7

^{QC Qc}y)(( ) = ^ j j ^QCy^{d T ds}

0 s

£ s +n

= 0^ j j d T ds = Q c y .

0 s

Это и означает, что оператор Q^c является проектором. Лемма доказана.

(LKpy \t ) = - - jj у (т) drds + jj у (т) drds, £nn

\

£

= у ^{( t} ) .

tt

(KL \t ) = - -J х "(r ^ds + j х "(r )drds = p'      £0000

t £t

=--- J ( х '( s ) - х '( 0 )) ds + j ( х '( s ) - х '( 0 )) ds =

£ 00

-- (х (£) - х (0) - £х '(0)) + х (t) - -х '(0) - х (0) = х (-)- х (0) = Pcx.

(pcK у)-) = --jsу(т)dTds + -sу(т)drds = х             £ 0000

= ^к, у .

Следовательно, оператор K_p обобщенным обратным оператором.

Оценим норму оператора K_p странстве W_p .

является

в про-

KpyW

—

1    ^s s

- -jj у(Т \d rd +||у||р =

^£  0 0

1    £

= — j (£ - s ) у (s )ds +1 |у||р.

^£  0

Используя неравенство Гёльдера, получим:

K p y_Wp

1    f£                1 q<т'П(£-s)qds} М,+1 к£  10

q ------- и q+1

+1   -I |у||р.

)

Лемма доказана.

Следующее утверждение доказано в работе [6]. Сформулируем его в удобной для нас форме.

Лемма 3. Для любого элемента x пространства W_p [0;1] справедливы неравенства:

1 x ⁽ t ) x w , x ^,( t ) xw •

Лемма 4. Пусть существуют неотрицательные постоянные a , b и неотрицательная функция g e L _M [ 0;1 ] , такие, что

|^{f ( t} , ^u 1 , ^u 2 ) <  a^u 1 1⁺ bu 2 1⁺ g ^{( t} )

почти всюду при t e [ 0;1 ] и u 1 , u 2 e R ¹ .

Тогда для оператора F справедлива оценка:

||Fx l p <  a ⁺ p\\xW , где a = ql ⁽| h||    ⁺|| g ||   ), в = a + b .

M       -^M

Доказательство. Действительно,

IIFxp <|ax(t) + bx'(t) + g(t)+ h(t)|p < <(lhL.+lMl1+(a + bIxW ■

Лемма доказана.

Произвольно зафиксируем элемент x e X 0 и определим непрерывное отображение Ф : R 1 ^ R 1 равенством:

£ s + п

ф(с) = j j (f (t, x(t) + c, x'(t)) + h(t )dds .

0 s

Лемма 5. Пусть выполнено следующее условие: существует u > 0, такое, что sig^i)f (t, ui, u 2 )-| |h||   > 0

L M

(или      sign ( u₁ ) f ( t , u 1 , u 2 ) +| h ^ <  0) при

|u |> u *, u 1 , u 2 e R ¹ и почти всех t e [ 0,1 ] . Тогда существует постоянная ~ = с ( x ) , удовлетворяющая неравенству

|~| < max {ci |, c2 } < u * + k01|x||   , такая, что Ф(~)= 0.

Доказательство. Пусть существует u * >  0 , такое, что sigrnu 1 ) f ( t,^u 1 ,^u 2^)-||<   >  ⁰

L M при lu| > u*. Положим с = u* + k0)|x||ff . Тогда для всех с > c1, справедливо x(t)+с > u *, а следовательно,     Ф(с) > 0 .    Аналогично

ф(с)< 0 для всех с < с2 = u * — k0|x^ .

Тогда в силу непрерывности функции

Ф существует постоянная ~ = с(x), удовле- творяющая неравенству

|~| <  ^тах{4 \с ₂|^} < u *^{+ k} 0I x W , такая, что ф ( ~ ) = 0.

В случае, когда выполнено условие sign(щ ) f ( t , u 1 , u 2 ) +1 h\\_L < 0 , доказательство проводится по той же схеме.

Лемма доказана.

Перейдем к доказательству теоремы 1.

Доказательство теоремы 1. Для доказательства теоремы проверим выполнение условий теоремы 2. Действительно, оператор L _– фредгольмов (лемма 1) и оператор F : W_p ¹ ^ L_p , определенный равенством

( Fx )( t ) = f ( t , x ( t ) + с , x ' ( t )) + h ( t ), вполне непрерывен.

Для проверки условия 3 теоремы 2 рассмотрим уравнение

QCF (x + u )= 0, где u e kerL , x - некоторый элемент X0 . Если при каждом фиксированном x e X0 данное уравнение имеет решение, то су(щ6)ест-вует элемент u e kerL , удовлетворяющий условию F (x + u ) e imL .

Имеем

1   £ s + n

QCF(x + u) = — f [f(x + u)(t)dt =

^£П ^J0 s

I ^£ s ⁺ n

= — Г I" (f (t, x(t) + с, x'(t)) + h(t)dtds = 0.

^£П 0 s

Для произвольно фиксированного элемента x e X _o исследуем функционал Ф , определенный равенством (6).

Из леммы 5 следует, что существует элемент ~ e ker L , удовлетворяющий требованиям F ( x ₀ + u ) e imL , || u || <  И l ^x ll ^{+ 3} , причем / = k ₀, 3 = u * .

Теорема доказана.