Об одной модификации схемы алгоритма in silico-картирования генома
Автор: Чечулин Виктор Львович, Боронникова Светлана Витальевна, Морозенко Владимир Викторович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Информатика. Информационные системы
Статья в выпуске: 2 (2), 2010 года.
Бесплатный доступ
Описан вариант модификации схемы алгоритма in silico-картирования генома для случая полигенной модели влияния генотипа на фенотип, и при наличии базовой и вариативной частей генома; указано на ограничения детерминистской модели контроля признаков.
Алгоритм in-silico картирования генома, полигенная модель, алгебра подмножеств генома, дерево корреляций, интерпретация теоремы гёделя о неполноте
Короткий адрес: https://sciup.org/14729665
IDR: 14729665 | УДК: 519.254;
Текст научной статьи Об одной модификации схемы алгоритма in silico-картирования генома
Предисловие
Алгоритмы in silico -картирования генов широко применяются в прикладной генетике [8]. В [1] описан алгоритм in silico -картирования генов, работоспособный только в случае моногенной модели наследования (моногенной модели влияния генома на фенотипические признаки). Как показали модельные и экспериментальные исследования, при полигенной модели наследования процесс идентификации не столь однозначен и полон [1]. Поэтому с учетом полигенной модели наследования [5], подтверждаемой широким набором экспериментальных фактов (см. напр. [3]), возникает потребность модификации этого алгоритма, учитывающего действительный характер наследования признаков. Модификация алгоритма in silico -картирования генов с обозначением условий его сходимости и описана ниже.
1. Модель наследования
Вообще возможные предполагаемые модели влияния генов на фенотипические признаки таковы:
-
1) моногенная модель (теоретическое предположение, алгоритм картирования генома в этом случае описан в [1]),
© В.Л.Чечулин, С.В,Боронникова, В.В,Морозенко, 2010
-
2) полигенная (подтверждаемая экспериментальными исследованиями, см. [2, 5]),
-
3) полногенная (маловероятный случай, если на фенотипический признак влияет вся совокупность генетического кода, не допускающий идентификации ввиду невозможности локализовать гены, влияющие на признак).
Полногенный случай является теоретическим предположением, отличным от реалий ввиду того, что геном имеет "облигатную часть, содержащую структурные и регуляторные гены, необходимые для нормального развития организма, и на факультативную, варьирующую часть, содержащую мобильные элементы разных классов, а также другие формы повторов" [4, 2], т. е. не все гены генома определяют набор фенотипических признаков организма, даже если имеются сети связанных генов, влияющих на фенотип [5].
При полигенной модели допустимы следующие очень приближенные предположения о геноме:
-
а) имеется базовая (облигатная) часть, задающая фенотипическую структуру организму (обеспечивающую его жизнедеятельность),
-
б) дополнительно к базовой части кода имеется вариативная часть, задающая вариацию фенотипических признаков.
-
в) базовая часть одинакова у разных линий одного вида, вариативная, соответст-
- а) геном, разбитый на 10 фрагментов (один из 252 вариантов разбиения), 1-й слой
1 2 3 4
5 6 7 8 9 10
-
б) варианты фрагментов (основной и дополнительный) на 2-м слое разбиения
1 2 3 4 5 6 7 8 9 10
|
KRt-z |
— |
— |
- - |
Рис. 1. Пример разбивки генома на 1-м шаге. При дальнейших шагах выделенный предыдущий фрагмент объединяется в непрерывный отрезок и для него производится аналогичная разбивка на части. Корреляция считается по выделенным фрагментам (и отдельно по их дополнению – невыделенным фрагментам) для каждого слоя разбиения венно различна; доля вариативной части не более чем доля базовой части генетического кода.
При таких, очень общих предположениях прозрачно строятся математические модели модифицированного алгоритма картирования.
На геноме, как на единице, задаваема некоторая дискретная сигма-алгебра А его подмножеств (не обязательно связных, допустимы и несвязные подмножества). Мера всего генома (длина) нормируется как единичная.
В первом приближении рассматривается множество А1i из А определенной меры (например 1/2, µ (А 1i )=1/2 ). Определяя коэффициент корреляции вариаций генотипа каждого множества А1i (в линиях генома) с вариациями фенотипа, можно выбрать множество А1k с максимальным коэффициентом корреляции и далее к нему (так же, как к множеству А) рекурсивно применить эти же рассуждения (на втором шаге µ (А 2i )=1/4 и т. д.).
Остановка алгоритма по достижению максимума означенного коэффициента корреляции имела бы место при унимодальном характере роста коэффициента корреляции, однако это предположение далеко от реальности. Поэтому требуется полный перебор всех подмножеств из А с конечным числом шагов, допустимым вычислительными ресурсами.
Рассмотрим алгоритм подробнее.
2. Описание алгоритма
Последовательность действий в упомянутом алгоритме такая же, как и в алгоритме in silico -картирования (см. подробное описание в [1]), с отличием в определении областей кода для вычисления коэффициента корреляции.
-
1. Из базы данных выбираются n линий с известными генотипами. У каждой из этих линий определяется количественное значение признака, характеризующего ее фенотип.
-
2. Формируются все возможные пары линий.
-
3. Для каждой пары линий i и j определяется разница фенотипов x ij .
-
4. Геном разбивается на районы [1] длиной около 1000 нуклеотидов (всего районов r), и для каждой пары линий i и j подсчитывается доля различающихся аллелей в каждом k -м районе.
-
5. В дальнейшем для выделенных отрезков (и их дополнений) производится такая
-
6. Строится 2-е дерево коэффициентов корреляций, количество слоев дерева ® log2 r (см. рис. 2).
-
7. На завершающем m-м слое этого 2-го дерева выбирается максимальный коэффициент корреляции и сравнивается с максимальным на (m–1)-м слое и т. д., выбирается максимальный коэффициент из максимальных по слоям и соответствующая ему выделенная область генома, в ней с максимальной вероятностной мерой, равной коэффициенту корреляции, находятся задающие фенотипический признак гены.
Эти районы группируются определенным образом, как указано ниже.
Далее следуют рассуждения для одного признака (для каждого признака повторяются).
При дихотомическом сужении области (предполагается, что вариативная часть не более чем ½ генома) геном разбивается на 1-м шаге на 10 равных отрезков1 (см. рис. 1) и выделяется половина этих отрезков (всего вариантов такого выделения половины отрезков С105 = 252). Корреляция между количеством различающихся аллелей и разницей фенотипов определяется по выделенным отрезкам для всех вариантов выделения. Выбирается вариант с максимальным коэффициентом корреляции corr("1", "0"). Аналогично параллельно вычисляются корреляции с дополнительными к выделенным отрезками (второй половиной при всех вариантах выделения). Так же выбирается вариант с максимальным коэффициентом корреляции, corr("1", "1").
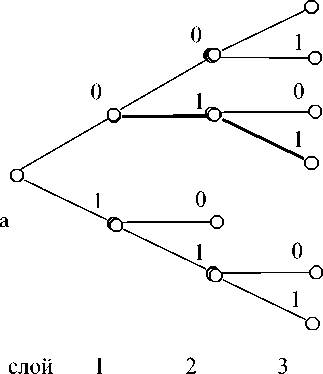
Рис. 2. Фрагменты 2-е дерева корреляций: а – корреляция со всей цепочкой кода, далее каждой максимальной, из вариантов разбивки, корреляции на слое s (шаге s–1) соответствует двоичное слово длиной s, например 011 (путь к ней выделен)
же дихотомия и вычисляются корреляции (по п. 4) при полном переборе возможных подмножеств их сигма-алгебры над А.
В итоге по максимуму коэффициента корреляции выделяется коррелирующий с вариацией фенотипического признака фрагмент генома (множество из сигма-алгебры А), содержащий гены, влияющие на этот признак.
3. О сходимости алгоритма
При полном переборе вариантов набора фрагментов генома 2 , коррелирующих с определенным фенотипическим признаком, очевидно, что существует фрагмент (область фрагментов, не обязательно связная) с максимальным коэффициентом корреляции, что и доказывает сходимость алгоритма в случае полного перебора всех вариантов выделения фрагментов генома3.
4. Заключение
Таким образом, при предположении о связи генотипа и фенотипа (непредикативный способ рассуждения4) возможно использова- ние модификации алгоритма. Описанный алгоритм аналогичен алгоритму поиска экстремума функции методом дихотомии, с учетом того, что множества, на которых задается функция (указанный коэффициент корреляции) на одном слое (шаге разбиения), имеют одинаковую меру (длину) и от слоя к слою их мера (длина) уменьшается вдвое.
Такая схема алгоритма позволяет картировать области генома (а не единичные гены, как в моногенной модели), связанные с фенотипическим признаком.
Теоретические положения об очевидной сходимости алгоритма подлежат экспериментальной проверке.
Список литературы Об одной модификации схемы алгоритма in silico-картирования генома
- Аксенович Т.И., Зыкович А.С. Оценка мощности in silico-картирования//Генетика. 2006. Т. 42, №6. С.850-857.
- Голубковский М.Д. Век генетики: эволюция идей и понятий, М.; СПб., 2000.
- Гончаров Н.П., Глушков С.А., Шумный В.К. Доместикация злаков Старого Света: поиск новых подходов для решения строй проблемы//Журн. общей биологии. 2007. Т. 68, №2. С.126-148.
- Евгеньев М. Б. Мобильные элементы и эволюция генома//Молекулярная биология. 2007. Т.41, №2. С.234-245.
- Cуслов В.В., Колчанов Н.А. Дарвиновская эволюция и регуляторные генетические системы//Вестн. ВОГиС. 2009. Том 13, №2. С.410-439.
- Чечулин В.Л. О приложениях семантики самопринадлежности//Вестн. Перм. ун-та. Сер. Математика. Механика. Информатика. 2009, вып. 3 (29). С.10-17.
- Чечулин В.Л. О кратком варианте доказательства теорем Гёделя//Фундаментальные проблемы математики и информационных наук: материалы междунар. конф. при ИПМ ДВО РАН, Хабаровск, 2009. С.60-62.
- Хесин Р.Б. Непостоянство генома. М.: Наука, 1984. 472 с.
- Dadashev S. Ya., Grishaeva T. M., Bogdanov Yu.F. In Silico Identification and Characterization of Meiotic DNA: AluJb Possibly Participates in the Attachment of Chromatin Loops to Synaptonemal Complex//Russian Journal of Genetics. 2005. Vol.41, №12. P.1419-1424.
- Chechulin V.L., Ardavichus V.G., Kolbasina O.V. Informatization of the process of producing formalin//Russian Journal of Applied Chemistry, MAIK Nauka/Interperiodica. 2008. Vol. 81. № 6. P1112-1116.


