Об одной нелокальной краевой задаче для нагруженного уравнения третьего порядка
Автор: Дзарахохов Азамат Валерианович, Елеев Валерий Абдурахманович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.6, 2004 года.
Бесплатный доступ
Доказаны существование и единственность решения нелокальной краевой задачи для смешанного нагруженного уравнения третьего порядка с кратными характеристиками для трех возможных случаев расположения корней характеристического уравнения.
Короткий адрес: https://sciup.org/14318120
IDR: 14318120
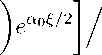
Список литературы Об одной нелокальной краевой задаче для нагруженного уравнения третьего порядка
- Нахушев А. М. Дробное исчисление и его применение.-М.: Физматлит, 2003.-271 c.
- Бицадзе А. В. Уравнения смешанного типа.-М.: Изд-во АН СССР, 1959.-164 с.
- Фадеев Д. К. Лекции по алгебре.-М.: Наука, 1984.-416 с.
- Джураев Т. Д. Краевые задачи для уравнений смешанного и смешанно-составного типов.-Ташкент: Фан, 1979.-238 с.
- Иргашев Ю. Некоторые краевые задачи для уравнений третьего порядка с кратными характеристиками//В сб.: Краевые задачи для дифференциальных уравнений и их приложения.-Ташкент: Фан, 1976.-С. 17-27.
- Джураев Т. Д., Сопуев А., Мамажанов М. Краевые задачи для уравнений параболо-гиперболического типа.-Ташкент: Фан, 1986.-220 с.
- Елеев В. А., Лайпанова А. М. Краевая задача для смешанного нагруженного уравнения гиперболо-параболического типа третьего порядка//Вестник СОГУ.-2003.-№ 2.-C. 14-22.
- Нахушев А. М. О задаче Дарбу для одного вырождающегося нагруженного интегро-дифференциального уравнения второго порядка//Диф. уравнения.-1976.-Т. 12, № 1.-С. 103-108.
Статья научная
