Об одной нелокальной краевой задаче для смешанного уравнения третьего порядка с кратными характеристиками

Доказана однозначная разрешимость нелокальной краевой задачи типа Бицадзе — Самарского для смешанного уравнения третьего порядка с кратными характеристиками.

Пусть Q — односвязная смешанная область плоскости независимых переменных x и у, ограниченная отрезками AA o , A o B o , B o B прямых x = 0, у = y o , x = l соответственно и характеристиками AC : x + у = 0, BC : x — у = l уравнения

0=

I

U xxx U xxx

- U y - λ 1 U, - U yy_x ,

у > 0, у < 0;

Q 1 = Q П (у >  0), Q 2 = Q П (у < 0). Через I обозначим интервал 0 < x < l прямой у = 0.

Задача 1. Найти функцию U (x,y) G C (Q) П C 1 (Q) П c X 3 y ¹⁾ (Q ₁ ) П с Х 3 У 2) (Q 2 ), удовлетворяющую уравнению (1) в Q i U Q 2 и краевым условиям

^аа 1 ⁽у) дх ^{+ в} 1 ⁽у^)и (^

= ^^а 2 ⁽у) ^ ^{+ в} 2 ⁽у^)и(x,y^)

+ ^(у),

^U | AC = ^ 1 ^(x),   ^AC = ^ 2 ^(x)i

0 6 x 6 |,

где ^ 1 (у), ^ ₂ (у), 5(у), ^ 1 (x), ^ ₂ (x) — заданные достаточно гладкие функции, x o G I , причем в 2 (у) = 0.

Общее решение уравнения (1) при у < 0 задается формулой

U (x,y) = F 1 (x + у) + F 2 (x - у) - ^(у),

где F 1 (x) G C 1 (I) П C 2 (I ), F 2 (x) G C(I ) П C ² (I).

Удовлетворяя (5) краевым условиям (4), получим x-y

- 2 y

У ^ 2 Q2 dt - (x+y)F 1 (0) — F 1 (0). 0

^{U (x},y⁾= ^F 1 ^(x+У⁾⁺^ 1 xx-— ) ⁺ ^1= У ^2 (j) dt - 2 0

(c) 2005 Дзарахохов А. В.

Дифференцируя (6) по x и y и вычитая из первого соотношения второе, а затем переходя к пределу при у ^ 0—, получим функциональное соотношение между т(x) и v (x), принесенное из гиперболической части Q2 на линию у = 0 в виде т 0(x) — v (x) = 9(x),

где

т(x) = lim U(x,y), v(x) = lim Uy(x,y), y→0-                 y→0- e(x) = Ф1 (|) + VN2 (I) - VN2(0).

Из уравнения (1) при у >  0 следует, что т (x) и v(x) будут связаны следующим соотношением, принесенным из параболической части Q i на линию у = 0

т ⁰⁰⁰ (x) — v (x) — А ₁ т (x) = 0.

Исключая v(x) из (7) и (8) и учитывая граничные условия (2) и (3) при у ^ 0+, получим нелокальную краевую задачу для обыкновенного дифференциального уравнения третьего порядка т000 (x) — т 0(x) — Ai т (x) = — 9(x),(9)

т(0) = rJ°i, т0(0) = ^2(0),

(а1(0)т0(x) + V(0)т(x)) |x=x0 = (а2(0)т0(x) + в2(0)т(x)) |x=l + 5(0).

Характеристическое уравнение, соответствующее однородному уравнению (9 = 0) (9), имеет вид k3 — k — Ai = 0.(12)

Введем обозначения s = -4 — 27 . Известно [1], что уравнение (12) имеет один действительный и два сопряженных комплексных корня, если s >  0. Оно имеет три различных действительных корня, если s < 0. При s = 0 все три корня уравнения (12) действительны, причем два из них равны. Рассмотрим случай, когда s >  0. В этом случае k i = u i + v i , k 2 = — k i + ih, к з = — k l — ih, где через u i , v i обозначена какая-нибудь пара значений кубических радикалов, причем h = ^23 (u i — v i ).

u = Vb^ I + V s, v = Vb^ ¹ + V s, удовлетворяющих соотношению uv = 3 .

Общее решение неоднородного уравнения (9) будем искать в таком же виде, как и общее решение соответствующего однородного уравнения (9 = 0) (9). Заменим произвольные постоянные некоторыми непрерывно дифференцируемыми функциями от x, т. е. положим

т (x) = C _i (x) exp(k _i x) + (C ₂ (x) cos hx + C 3 (x) sin hx) exp

(^— t) x

Выберем функции C i (x), i = 1, 2, 3, так, чтобы т (x), определяемое формулой (13), было общим решением уравнения (9). На основании общей теории [2], для определения C i (x) получим следующую систему дифференциальных уравнений

C i (x)z i + C 2 (x)z i + C 3 (x)z 3 = 0, 00 00 00

< C i ^(x)z i ⁺ C i ^(x)z 2 ⁺ C 3 ^(x)z 3 = ⁰,                               ⁽¹⁴⁾

P0      0,0! 1             0,0! 1 pl      0,11 _

Ci(x)zi + C2(x)z2 + C3(x)z3 = —9(x), где z1 = exp(k1x), z2 = cos hx exp(- k21 )x, z3 = sin hx exp(- k21 )x фундаментальная система решений однородного (θ = 0) уравнения (9).

Система (14) есть алгебраическая линейная неоднородная система относительно C _i ⁰ (x). Разрешая эту систему относительно C _i ⁰ (x), находим

C i ⁰ (x) =

W ni (x)θ(x) W(x)

где W _ni (x) — алгебраическое дополнение элементов n-й строки определителя Вронского.

W(x) =

-

- ₂ ¹ cos hx - h sin hx ) (( ^k ₄ ¹² - h ² sin hx - k 1 h cos hx

k 1     ^k ₄ ^{1 2} - h ² cos hx + k 1 h sin hx

причем

+ cos hx h cos hx

+ sin hx

-

₂ ¹ sin hx ^¶ k ₁ ²

-

k 1     ^k ₄ ^{1 2} - h ² sin hx - k 1 h cos hx

k 1

cos hx + k 1 h sin hx - k 1 ( - ₂ ¹ cos hx - h sin hx     6 = 0,

W 31 (x) = - k 1 h exp( - k 1 x), 3                  k 1

W 32 (x) = (h cos hx - ₂k 1 sin hx) exp( ₂ x), 3                              k 1

W 33 (x) = - (₂k 1 cos hx - hsin hx) exp( ₂ x).

Интегрируя равенство (15) от 0 до x, получим

x

^Z W ni (t)θ(t)dt C i (x) = -       _{W ( t )}     +γ i ,

i=1,2,3,

где γ i — произвольные постоянные. Подставляя (16) в

(13), находим

3 ^x τ(x) = -^X z i i =1    ₀

W ni (t)θ(t) dt W(t)

+     γ i z i .

i =1

Удовлетворяя (17) граничным условиям (10), (11), получим алгебраическую линейную неоднородную систему относительно γ i , i = 1, 2, 3, с определителем

∆ = (Θ1 - CΘ2)h - 2k1Θ3, где

+ a ₂ (0) ^ ^h sin hl + ^1 cos hl^ — в 2 (0) cos hl^ exp ^—^1l^ ,

■ ^a - (0) ^h cos hx o — — ^a ₂ (0) ^h cos hl —

-1- sin hxo^ + в 1 (0) sin hxo^ exp ^— -1- xo^ 21- sin hl^ + в ₂ (0) sin hl^ exp ^—^¹l^ .

Разрешая эту систему относительно γ i , находим

Y 1 = A ¹ ^(5 - — ^ i (0)© ₂ ) — ^ ₂ (0) + n ⁰ (0) — 1 ^ 1 (0)J

Y 2 = A ^-1 ( (^ 1 (0) — 5 1 )h + (^ 2 (0) + n ⁰ (0) — ^ 1 (0))© з ) ,

Y 3 = A ^-1

((— 251 + йОТ (©2 + ©-))

^— n ^{0 (0))}),

если A = 0.

После определения т(x) в области Q 1 приходим к задаче (1), (2), u(x, 0) = т(x), u(l,y) = ^ з (у). Решение этой задачи дается формулой (4).

где

(x, y)

U (x,y) = v(x,y) — А

π

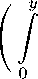
G ₅₅ ^(x,y;⁰,n⁾^ 1 ⁽n⁾ dn

ly

^Z ₀ dξ ^Z ₀

-

G^(x,y; €,n^)U(€,n) dn,

λ

λ 1 π^,

-

y j Gs(x,y;0,n)^2(n) dn

y j G^ (x,y; l,n)^3(n) dn +

l j G(x,y; С,0)тШ d£

G(x,y; C,n) — функция Грина рассматриваемой задачи для уравнения U _xxx — U y = 0. Метод построения и ее основные свойства даются в работе [4]. Решение интегрального уравнения (18) можно выписать через резольвенту R(x,y; C,n) ядра AG(x,y; С, n)

U (x,y) = v(x,y) +

yl

^Z ₀ dη ^Z ₀

^R(x,y; ^c,n ^{) v ( c,}n) d^c-

Реализуя краевое условие (3), получим интегральное уравнение относительно функ- ции ^з(у)

y e2(y)^3(y) +

j M ^(x,n⁾^ 3 ⁽n⁾ dn = g⁽y), 0

где ядро M (x,n) и правая часть g(y) уравнения (20) выражаются через функцию Грина G, резольвенту R и заданные функции (3).

По условию в 2 (у) = 0. Таким образом, уравнение (20) является интегральным уравнением Вольтерра второго рода, которое безусловно и однозначно разрешимо в классе C (0 6 у 6 у о ).

После определения функции ^з(у), решение задачи 1 в области Qi находим по формуле (19), а в области Q2 приходим к задаче (1), (4), u(x, 0) = т(x), единственное решение которой дается формулой x+y                    2y

^U(x, у) = ^т(x + у) ^- ^ 1 ^x+y) + ^ 1 x^-^"-^ j ^ 2 Q) ^dt -^ j Mt) ^dt, x - y                     0

где т (x) определяется из (17).