Об одной новой методике решения одного класса модельных интегро-дифференциальных уравнений первого порядка с сингулярным ядром

DOI:

Теория интегро-дифференциальных уравнений и интегро-дифференциальных уравнений с сингулярными коэффициентами является одним из важных разделов теории интегральных и дифференциальных уравнений, которые находят широкое и многообразное применение в физике и технике.

Многие задачи прикладного характера, например задача Вольтерра о крутильных колебаниях, задача Прандтля расчета крыла самолета, задача об изучении кинетического уравнения Больцмана, приводят к изучению сингулярных интегро-дифференциальных уравнений [4–6; 10–12]. Также в последние годы в силу своей прикладной важности изучаются прямые и обратные задачи для интегро-дифференциальных уравнений [7; 16; 19; 20], а также разрабатываются методы для исследования разных классов вырождающихся интегро-дифференциальных уравнений в банаховых пространствах [1–3; 17; 18].

Важно заметить, что во многих исследованных сингулярных интегро-дифференциальных уравнениях существующие там интегралы понимаются в смысле главного значения по Коши, и поэтому для решения этих уравнений применяются методы теории аналитических функций. В случае, когда в сингулярных интегро-дифференциальных уравнениях интегралы понимаются в обычном смысле Римана, известно сравнительно мало работ.

В связи с этим в последние годы в работах Н. Раджабова [13–15] появилась новая методика для изучения интегральных уравнений типа Вольтерра с сингулярным и сверхсингулярным ядром. Эта методика была нами перенесена для изучения интегро-дифференциальных уравнений с сингулярным и сверхсингулярным ядрами в работах [8; 9].

В данной работе предлагаем новую методику решения одного класса обыкновенного интегро-дифференциального уравнения с сингулярным ядром и на основе полученных результатов исследуем граничные задачи для этих уравнений.

Постановка задач и их решение

Пусть Г = { х : a <  х <  b } - множество точек на вещественной оси. На Г рассмотрим модельное интегро-дифференциальное уравнение:

ф'(х)+— x

A

—

x

- ф(х)+J ■ a

a

B- ф'() + / C X2 ф!/) dt = f(х), t — a       (t — a)

где A , B , C - заданные постоянные числа; fх ) - заданная функция; ф ( х ) - искомая функция.

Прежде всего через C a [ a , b ] обозначим класс таких функций, которые имеют производную первого порядка, и в точке x = a обращаются в нуль с асимптотическим поведением

ф(х) = о[(х — a)Y1 ] , у, > 1, а первая производная от этих функций в точке x = a обращается в нуль с асимптотическим поведением ф'(х) = о [(х — a)Y2 ] , у2 > е , где е > 0 и решения уравнения (1) будем искать в этом классе.

В данной работе будем исследовать уравнение (1) в случае, когда коэффициенты этого уравнения связаны между собой равенством C = A • B . В этом случае уравнение (1) можно записать в таком виде:

ф'(х)+

A

x

—

a

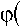
x

х )+J А t — a

a

ф,(t)+-A- ф(t) t—a

^dt = f ^{( х} ) .

Если введем обозначение ф' ( х ) + A ф ( х ) = ф ( х ) , тогда приходим к решению следующей

х — a системы интегро-дифференциальных уравнений:

ф'(х) +      ф(х) = ф(х), х — a xB

v(х)+ [----v(t) dt = f (х).

^J t — a

Как видно из (3), первое уравнение этой системы является дифференциальным уравнением, а второе – интегральным уравнением с сингулярным ядром. Эти уравнения в отдельности хорошо изучены в работах Н. Раджабова [13–15]. Используя эти результаты решения системы (3), получим следующие случаи:

I. Пусть B <  0 , тогда решение уравнений системы (3) дается по формулам:

х Л      X ^— A

ф ( х ) = ( х — a ) ^— A с , + Г I -—- I v ( t ) dt , ^JI t — a )

a xB

у(х) = (х — a)s с2 + f (х)—B П----1 j-^-dt.

^JI t — a ) t — a a

Для получения решения уравнения (2) в первом равенстве (4) вместо ф ( x ) , подставляя его значение из второго равенства, получим:

x / х - A

ф(x) = (x - a)-Aq + [I x—a |

³1 t - a ) a

tB

(t - a)B с2 + f (t)- B [ I| —— dт 3lт-a) т-a

a

dt .

После некоторых преобразований решение вида (5) легко можно записать в таком виде:

Ф⁽ x ) = ⁽ x

- a) Ac1 +(x - x

+        '         •

I ^B | + ^A + ¹ I

a) B+1, , с2      +

’   |B + A + 1

( . , / x - a

( A + 1 )-----

( t - a

- A

+

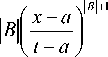
f ^{( t} ) dt = / ;[ c 1 , c 2 , f ⁽ x ^)]

Не ограничивая общности, предположим, что 1 < - A <  B | + 1. В этом случае для сходимости интегралов в правой части (6) требуем, чтобы функция f ( x ) в точке x = a обращалась в нуль с асимптотическим поведением:

f ⁽ x ) = o ^[( x - a ^{) S 1 ]} , 51 > | B |.

Таким образом, доказана следующая теорема.

Теорема 1. Пусть в интегро-дифференциальном уравнении (1) коэффициенты А, В и С между собой связаны равенством C = A ■ B и они такие, что выполняется неравенств о B <  0, 1 < - A <  B | + 1 . Функция fx ) в точке x = a обращается в нуль с асимптотическим поведением (7).

Тогда однородное уравнение (1) имеет два линейно независимых решения, а неоднородное уравнение (1) в классе функций y ( x ) е C a [ a , b ] , обращающихся в нуль в точке x = a, всегда разрешимо, и его общее решение содержит две произвольные постоянные, и дается по формуле (6).

Замечание 1. Подобное утверждение можно получить в случае, когда вместо условия 1 < - A < | B | + 1 выполняется условие 1 <  B + 1 < - A.

Теперь пусть выполняется неравенство - A <  1 <  B | + 1. В этом случае из выражения (6) следует, что если решение уравнения (1) при - A <  1 существует, тогда для того чтобы оно принадлежало классу C a [ a , b ] , произвольная постоянная c ₁ должна быть равна нулю, то есть в этом случае решение уравнения (1) имеет вид:

- A с2           1 x ( , 1/x-a

+;( A + 1 )

I B | + A +1 | B | + A + 1 a ^v     \ t - a.

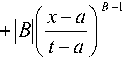
f ( t ) dt =

ф ( x ) = ( x - a ) ^{B +} = ^ Г [ 0, c 2 , f ( x )].

В этом случае тоже для сходимости интегралов в правой части (8) функция f ( x ) должна обращаться в нуль с асимптотическим поведением (7).

Таким образом, имеет место следующая теорема.

Теорема 2. Пусть в интегро-дифференциальном уравнении (1) коэффициенты А, В и С между собой связаны равенством C = A ■ B и они такие, что выполняется неравенств о B <  0 , - A <  1 <  B | + 1 . Функция f(x ) в точке x = a обращается в нуль с асимптотическим поведением (7).

Тогда однородное уравнение (1) имеет одно линейно независимое решение, а неоднородное уравнение (1) в классе функций y ( x ) е C \ [ a , b ] , обращающихся в нуль в точке x = a, всегда разрешимо, и его общее решение содержит одну произвольную постоянную c ₂ , и дается при помощи формулы (8).

II. Пусть B >  0, тогда формальное решение уравнений системы (3) дается по формулам:

х А      X - A

ф(х) = (х - a)-A с, + [I -—- I ^(t>, JI t - a )

a

ф(х) = (х - a)-Bс2 + f (х)- B ff X—a| f^-dt.

•X t - a ) t - a

a

Так как во втором равенстве этой системы слагаемое ( х - a ) B e 2 не принадлежит классу C a [ a , b ] , поэтому мы должны взять с 2 = 0 и значения

( \ Н \ о Г ( х - a ) B f ( t ) , ф ( х ) = f ( х ) - B II----I —— dt

* \ t-a ) t-a , a подставляя в первое равенство системы (9), после некоторых преобразований решение уравнения (2) получим в таком виде:

ф(х ) = (х - a) Ac1 + =e;[a,o, f (х)!

A - B +1

х         /      X- A

J (A+1)f     I

я It - a )

-

B

t - a

х - a

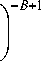
f ( t ) dt =

Если - A >  1, тогда для сходимости первого интеграла в правой части (10) требуем, чтобы функция f ( x ) в точке x = a обращалась в нуль с асимптотическим поведением:

f (х) = о [(х - a )52 ] , 52 > - A -1.

Таким образом, имеет место следующая теорема.

Теорема 3. Пусть в интегро-дифференциальном уравнении (1) B >  0 и коэффициенты A, B и C между собой связаны равенством C = A • B. Кроме того, пусть функция f ( х ) е C [ a , b ] и в случае - A >  1 в точке х = a обращается в нуль асимптотическим поведением (11).

Тогда однородное уравнение (1) имеет одно линейно независимое решение, а неоднородное уравнение (1) в классе функций у ( х ) е C a [ a , b ] , обращающихся в нуль в точке х = a, всегда разрешимо, и его общее решение содержит одну произвольную постоянную c ₁ и дается при помощи формулы (10).

Объединяя вышеприведенные результаты для интегро-дифференциального уравнения (1), можно построить аналог об альтернативе Фредгольма в следующем виде.

Аналог теоремы об альтернативе Фредгольма для интегро-дифференциального уравнения (1): Если в интегро-дифференциальном уравнении (1) коэффициенты A, B и C между собой связаны равенством C = A • B и они такие, что выполняются неравенства B < 0 , 1 <- A <| B | + 1 , то однородное уравнение (1) имеет два линейно независимых решения и его общее решение содержит две произвольные постоянные, а неоднородное уравнение (1) разрешимо тогда и только тогда, когда его правая часть удовлетворяет условию (7). В этом случае неоднородное уравнение (1) имеет бесконечное число решений и его общее решение зависит от двух произвольных постоянных, и дается по формуле (6).

Если выполняются неравенства B <  0 , - A <  1 <  B | + 1 , то однородное уравнение (1) имеет одно линейно независимое решение и его общее решение содержит одну произвольную постоянную, а неоднородное уравнение (1) разрешимо тогда и только тогда, когда его правая часть удовлетворяет условию (7). В этом случае неоднородное уравнение (1) имеет бесконечное число решений и его общее решение содержит одну произвольную постоянную, и дается при помощи формулы (8).

Если выполняется неравенство B >  0 , то однородное уравнение (1) тоже имеет одно линейно независимое решение и его общее решение содержит одну произвольную постоянную, а неоднородное уравнение (1) разрешимо тогда и только тогда, когда его правая часть удовлетворяет условию (11). В этом случае тоже неоднородное уравнение (1) имеет бесконечное число решений и его общее решение содержит одну произвольную постоянную, и дается при помощи формулы (10).

Постановка и решение граничных задач

Вначале изучим свойства решений уравнения (1). Для этого введем следующие обозначения:

Pa [ ф ( x )] = / ¹ у A ф ⁽ x) PaB И x ^)] = 7---1У + В Т d- ₍¹ у A ф ( x )

( x - a )                     ( x - a )     dx L ( x - a )

Pb>(x )]= Z   \ Bl+1 ф(x )

( x — a )

Тогда имеют место следующие замечания.

Замечание 2. Решение вида (6) обладает свойствами:

^[ PA ^[ ф ⁽ x ^)]L = a = cV; ^[ PaB И x ^{)] ]} x = a = c 2 .

Замечание 3. Решение вида (8) обладает свойством

PaMx)]1.

c ₂

A + | b| + 1 •

Используя полученные интегральные представления и свойства данных решений для уравнения (1), можно ставить и решать граничные задачи типа Коши.

Задача А 1 . Требуется найти решение уравнения (1) из класса C [ a, b ] по следующим условиям:

[Pa [ф(x)]]x=a = 4, [Pa,B [ф'(x)Hx = a = B2, где B^ (j = 1,2) - заданные постоянные числа; PA [ф(x)], P^B [ф'(x)] - функции, определенные в (10)^

Исследование задачи А₁. Пусть выполнены условия теоремы 1. Используя интегральное представление (6) и его свойства (11), находим постоянные с ₁, с 2 : c₁ = B,, c 2 = B 2 .

Подставляя значения с ₁, с ₂ в (6), получим

ф ( x ) = E 1 ⁺ [ B\, B 2 , f ( x ) ] .                                         (13)

Таким образом, о решении задачи А ₁ справедливо следующее утверждение.

Теорема 4. Пусть коэффициенты и правая часть уравнения (1) удовлетворяют всем условиям теоремы 1. Тогда задача А₁ имеет единственное решение, которое выражается формулой (13).

Задача А 2 . Требуется найти решение уравнения (1) из класса C a [ a , b ] по следующим условиям

IPB| [ф

Исследование задачи А₂. Пусть выполнены условия теоремы 2. Используя интегральное представление (8) и его свойства (12), находим постоянную с₂:

[^S| ^[Ф⁽x)][=a = A + |B| ₊1 = B2 ^ c2 = (A⁺ |B| ⁺1)B2 .

Подставляя значения с₂ в (8), получим

Ф( x) = E ,⁺[0, (A + |B| +1)B 2, f (x)].                                   (14)

Таким образом, о решении задачи А₂ справедливо следующее утверждение.

Теорема 5. Пусть коэффициенты и правая часть уравнения (1) удовлетворяют всем условиям теоремы 2. Тогда задача А₂имеет единственное решение, которое выражается формулой (14).

Замечание 4. Подобную задачу можно решить для нахождения с₁в решении вида (10).