Об одной оценке для произведения B М. М. Джрбашяна
Автор: Таварацян Теймине Ваниковна
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 3 т.24, 2022 года.
Бесплатный доступ
В середине 60-х гг. М. М. Джрбашяном был предложен новый метод для определения и факторизации обширных классов функций, мероморфных в единичном круге. Эти классы, которые обозначаются через N{ω}, обладают сложной структурой и охватывают все мероморфные в единичном круге функции за счет того, что зависят от функционального параметра ω(x). Они переходят в классы Nα в случае ω(x)=(1-x)α, -1
Произведения джрбашяна, произведения бляшке, выпуклые последовательности, класс функций ω0, ряд фурье
Короткий адрес: https://sciup.org/143179304
IDR: 143179304 | УДК: 517.53 | DOI: 10.46698/n0335-8321-3720-b
Текст научной статьи Об одной оценке для произведения B М. М. Джрбашяна
1. Некоторые сведение о произведениях Джрбашяна
М. М. Джрбашяном в [1, 2] предложен метод для определения и факторизации классов функций, мероморфных в единичном круге. Эти классы обозначаются через N {ш}. Они переходят в классы N a в случае ш(х) = (1 — х) а , — 1 < а < +то, а в специальном случае ш(х) = 1 класс N {ш} совпадает с классом N Неванлинны.
О поведении мероморфных функций классов N ω можно прочитать также в книгах [3–6]. Отметим, что в последние годы получены некоторые интересные результаты о поведении функций классов N ω (см., например, [7–9]).
Пусть D — единичный круг комплексной плоскости C, Q — класс функций ш(х), удовлетворяющих условиям:
-
1) ш(х) положительна и непрерывна на [0; 1);
-
2) ш(0) = 1, / 0 ш(х) dx < +то,
Q q — подмножество тех функций из Q, для которых ш(х) не убывает на [0,1).
Далее, пусть Д о = 1, A k = kJ w(x)x k-1 dx, к = 1, 2,... , и пусть последовательность 0
{a k } ∈ D такая, что удовлетворяется следующее условие Бляшке — Джрбашяна:
∞ 1
/ w(x) dx < +то.
(Б-Дж)
k =1 |ak|
Произведение М. М. Джрбашяна с нулями на этой последовательности определяется следующим образом (см. [1, 2]):
вш (z) = вш (z; {ak}) = [[ A (z; {ak}), ^(x) e Q, k где для |z| < 1 и 0 < |Z| < 1
A u (z; z) = ^1 - zj exp {- W(z; z) } ,
W (z,Z ) = У | ζ |
w(x)
x
dx
-
∞
| ζ |
∞
E z - k ^)
k =1
x k - 1
dx
— Zk / ш(х) x k 1 dx > -z—. J Ak
| ζ |
Заметим, что (см. [2, с. 97])
W i (z,Z ) = W (z,Z )U 1
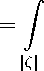
dx x
∞
— E J< z) k k =1
∞
- ln|z 1 - E k=1
(z z) k
k
Так как (см. [2, с. 51])
A i (z; z ) = A(z; Z ) = • , Izl < 1, 0 < IZ| < 1,
1 — Zz z то произведение Вш(z; {ak})-Джрбашяна при w(x) = 1 совпадает с произведением Бляшке:
B i (z; {a k }) = B(z; {a k }) = B(z) = П ^k—z • •
1 — a k z a k k =1
Известно, что (см. [2, с. 56]) если ^(x) не убывает на [0,1), то имеет место следующее представление:
2 n '
B u (z; {a k }) = B (z; {a k }) exp <
— [ S (e -iY z; ^) d^(Y) > ,
2n J где ^(y) — некоторая неубывающая ограниченная функция на [0;2п], и
∞ k
S (z; w) = 1+2 E 7“, | z | < 1, k =1 A k
— ядро Джрбашяна типа Шварца.
Если w(x) не убывает на [0,1), то ReS ш (z) ^ 0 (см. [2, с. 28]), и, следовательно, из представления В ш (z; {a k }) = Ик А ш (z; {a k }) имеем
\Б Ш (z; a k )| С |B (z; a k )| .
Последовательность {a k } k =o называется выпуклой, если, полагая Aa k = a k — a k +i , A2a k = Aa k - Aa k +i , имеем A 2 a k ^ 0, k = 0,1,... Как известно (см. [10, с. 100]), если a k ^ 0 и последовательность {a k } k =o выпуклая, то ряд 0 2 0 + 52^ =1 a k cos kx сходится всюду, кроме быть может x = 0(mod2n), к неотрицательной суммируемой функции f (x) и является рядом Фурье от этой функции.
2. Основные результаты
Пользуясь методом доказательства одной леммы В. С. Захаряна [11], докажем следу- ющее утверждение.
Лемма 1. Пусть ш(х) — неубывающая дифференцируемая функция из класса
^ 0 -
Тогда для любых z, Z (|z| < 1, 0 < |Z| С 1) имеет место следующее неравенство:
и ш (z; Z ) = Re
W ш (z, Z) — W 1 (z, Z) + ^A 2
-
-
x
| ζ |
dx
> 0.
<1 Из вида (1) функции W ш (z,Z ) имеет место
W ш (z,Z) — W i (z,Z) +
(Af ')/
| ζ |
-
= щ(х) x
| ζ |
dx
∞
-
w(x) — 1
| ζ |
x
∞
E Z - k / w(x) 71
k =1
j Хdx+Е k (Zz)k +
| ζ |
k =1
∞
dx
+
k =1
* 1 (Zz) k
k
-
A k
x k - 1
dx
-
Zk I Цх)
x
k - 1
dx
z k
(Af XI
ζ - k z k
| ζ |
w(x) — 1
x
dx =
| ζ |
| ζ |
jw(x)x k -1
A k
A 2 Г w(x)
At/ x
dx - ζ k z k
-
dx
| ζ |
j ш(х)х
k - 1
dx
| ζ |
Обозначим |Z| = r, l = zZ (|l| = r|z|, |z| < 1)). Тогда
ζ - k z k
= C -k z k Z k Z
k
= z k Z k Z - k Z - k = (zZ ) k (|Z| 2 )
k
= l k r
2 k
,
W ш (z,Z) — W i (z,Z) +
(A -И
w(x) — 1
x
dx
= A 2 f At/
| ζ |
| ζ |
w(x) — 1
∞
x
dx +
k =1
l k
k
-
r
A k
l k r
2 k
j w(x)
x k - 1
dx
-
lk j w(x)x
k - 1
dx
r
△
△ 2 У
w(x) — 1
x
| ζ |
∞ dx + £ k=1
|l| k
—— [cos(k • arg l) + i sin(k arg l)] k
r
-
△ k
Далее,
U u (z;z)
= △ f
△ 2J
| ζ |
Пусть
-
—— |l| k [(cos(k arg l) + i sin(k arg l)] • r 2 k [ w(x) △ k J
-
|l| k cos
|l| k [cos(k arg l) + i sin(k arg l)] j w(x)
x
k - 1
r
_ A2 /"
△ 2 У
w(x) — 1
x
| ζ |
r
x k - 1
dx
dx
∞ dx + £ k=1
|l| k
—— cos(k • arg l) k
(k arg l) • r 2k j w(x)x k 1 dx — |l|
∞
+ i sin(k arg l)
= Re
k
cos
(k arg l) У w(x)x
r
k - 1
dx
r
k =1
-
-1- |l| k sin(k arg l)r -2k [ ш(х)
△ k J
-
x k - 1
dx
|l| k sin(k arg l) I w(x)x
k - 1
dx
r
W u (z, Z) — W 1 (z, Z) + ^ д|
w(x) — 1
∞
-
∞
x
-
-
x
| ζ |
dx
|l|k dx + У2 * ,7" cos(k • arg l)
|l| k cos
-
k =1
(k arg l) У w(x)
+ УУ |l| k cos(k • arg l)
k =1
U u (z; Z ) = Re
r
k
-
r
x
k - 1
dx
△ k
r
2 k
△ k
r
|l| k cos
(k arg l) • r 2kj ш(х)
△ 2 f
△ 2 У
w(x) — 1
x
dx
| ζ |
j ^(x)x k 1
dx
-
W u (z, Z) — W l (z, Z) + ^ д | — 1^ У
| ζ |
j ^(x)
x
k - 1
r
w(x) — 1
x
dx
a o (r)
∞
x k - 1
dx
.
+ УУ a k (r) • |l| k cos(k arg l),
k =1
dx
где
a o (r) = 2^ У ^x; - 1 dx, r
, A 1 a k (r) = k -
A k
r
2 k
r jw(x)xk-i 0
dx
-
j w(x)x~k - i dx >
r
к = 1, 2, 3 ...
Для того чтобы установить справедливость неравенства (1), сначала установим
вы-
пуклость последовательности {a k (r)} o° , т- е. справедливость неравенств
W (r) = A 2
a k (r) = a k (r) - 2a k +i (r) + a k +2 (r) > 0,
0 < r < 1, k ^ 0.
то
Покажем справедливость неравенства (3) в случае к = 0, т. е. докажем, что
V o tr) = A 2
a o (r) = a o (r) - 2a ? (r) + a 2 (r) > 0.
Так как
a 1 ( r ) = 1
a 2 (r) = 2
r
-
-
A 1
r
У w(x) dx
-
j w(x)x 2 dx I ,
r
r
A 2
r
d
-
j w(x)x 3 dx I ,
r
^ 0 (r)
-2 A 2 A ?
f w(x)
x
-
dx
-
r
r
+
Значит
^ 0 (r)
-
2 A 2
2 A ?
(^(rr-^)
+ Ai *
-
A 1
-
- r
A 2
r
r
r
j w(x) dx
-
r
j .(x)x -2 dx
r
j ,(x)xdx
-
У w(x)dx +
r 2 ш(т)
r
-
A 2
-
2 r
j .(x)x - 3 dx
r
j .(x)xdx +
r
3 w(r) > .
Имея ввиду, что
r
r
ω
(r) -1 = у d(^(x)),
1 .(x) ax = „и
-
r
2 У w(x) • xdx = г2ш ( г )
r
j xd(y(x)),
r
из (5) получаем
r
-
j x 2 а(ш(х)),
^ o (r) =
-
2 A 2 2
r A J d(^(x)) + A
-
r
-
A 2
r
-r
-
r 2 ω
2r - 3
rω
r
(r) — У xd(w(x)) + 2r
2 ш(г)
(r) — у x 2 a(^(x)) +
r 3 ш(т)
2 A 2 2 2
r A1 / d("(x)) + r5 7 r
-
r
r
j xd(w(x))
r
2A 2 f p r J U1
-
Таким образом,
r
-
A 2 A 1
^ 0 (r) =
-
2A 2 г p r J U1
-
xr
A 2
r r A2
У x 2 a(^(x))
r
2 x +
A 2 r
4 x 2
^ a(^(x)). (6)
2 ^ d(w(x)).
Так как w(x) не убывает на [0,1), то из (6) следует, что ^ 0 (r) С 0. Это означает, что
на [0,1] функция ^ o (r) не возрастает, и, следовательно, ^ o (r) ^ ^ о (1), 0 < r < 1. Отсюда,
так как ^ о (1) = 0, следует справедливость неравенства (3) в случае к = 0.
Теперь докажем неравенство (3) для к ^ 1. Для этого запишем функции a k (r) (k ^ 1)
в виде
a k (r) = b k (r) + d k (r),
где
b k (r) = 1 k
-
r 2
r
A k
2 k
У w(x)
x k - 1
dx,
d k (r) = *
A k
У ш(х)
x
k - 1
dx
-
r
2 k
r
У w(x)
x k - 1
dx
r
r 2
В отдельности установим выпуклость последовательностей {bk(r)}”, {dk(r)}” путем проведения непосредственных оценок. Для этого сначала покажем что эти последовательности неотрицательны. Из (8) имеем bk (r) =
A k
1 w(r 2 ) — kr 2k 1
r 2
j w(x)x k - 1 dx
Так как ш(x) — неубывающая функция на [0,1), то r2 2k
ш(x)xk - 1 dx < ш(г 2 ) r—, 0 < r < 1. k
Следовательно, b'k(r) ^ 0, когда r Е (0,1). Значит функция bk(r) (к = 1, 2,...) является невозрастающей функцией на [0,1]. Но bk(1) = 0, к = 1, 2,... Следовательно, для любого натурального числа k имеем bk(r) > 0, 0 Далее, так как ш(x) — неубывающая функция на [0,1), то ^[r-k — 1], Jши x-k-1 dx> r r r2j ш(x)xk-1 r2 dx ^ r-2kш (r) xk-1 dx ~Tr~(r —k — 1). k Значит для любого натурального числа к и для любого r Е (0,1) dk(r) > 0. Теперь, записав формулу (8) в виде bk(r) = 1 — ^ JQ1 ш(r2x) xk 1dx, имеем A2bk (r) = bk (r) — 2bk+1(r) + bk+2(r) = 1 — —— I ш(r2x)xk1dx — —-— AkJ V ’ к + 1 о +——— / ш(r2x)xkdx + — / ш(r2x)xk+1dx = —----Ak+1J ’ к + 2 Ak+2 J ’ k(k + 1)(k + 2) о0 — —[ ш(r2x)xk-1dx + ——— [ ш(r2x)xkdx ——-— [ ш(r2x)xk^1dx AkJ Ak+1 J v ' Ak+2 J v ' 0 00 = 7 / ш(r2x)xk-111 — 2 ^k x + ^k x2! dx. k(k + 1)(k + 2) AkJ v ’ I Ak+1 Ak+2 J о Для любого x имеем (см. [2, с. 30–31]) Поскольку при w(x) G Qo, w(r2x), 0 < r < 1, 0 С x < 1, является возрастающей функцией от r, то из (12) и (13) получим неравенство Л2bk(r) > Л2Ь/г(1) = —----[ w(x)xk-1dx кх кх ’ k(k + 1)(k + 2) Лк J v Лк+1 У ш(x)xkdx — Лк+2 / ^(x)xk+1dx = k(k + 1)(k + 2) - 1 2 к+к - к + 2 = 0. Итак, отсюда и из (10) при 0 < r < 1 получим Ьк (r) > 0, Л2Ьк (r) > 0, к = 1, 2, 3,... Далее, из (9) имеем Л2dk(r) = dk(r) - 2dk+i(r) + dk+2(r) - Лк 2 V Лк+1 + 1 Лк+2 У w(x)x-r k-1dx j w(x)x- r -r r 2k j ш(x)xk-1dx r2 r k-2dx + r-2k-2 у ш(x)xkdx r2 Уw(x)x к 3dx r - r r-2k-4 j w^1 dx r2 = Л;/"<x)x-r k-1 1- Л1 2 \ '' " + Лк+1 x Лк Лк+2 X2 _ dx - r Лк r 2кI ш(х)хк-1 r2 1- 2Лк x Лк+i r2 + Лк x2 Лк+2 Г4 _ dx. Но выражения, стоящие в подинтегральных квадратных скобках справа в (15), неот- рицательны в силу неравенства (13). w(x) G Qo не убывает на [0,1), из (15) Поэтому, учитывая еще, что функция w(x) при получаем следующую оценку: Л2dk(r) > w(r)-^ < Лк /x-k-1[1 -2 r Лк 1 , Лк 11 Лк+i x + Лк+2 X2] dx r 2к [тк-1 |"l _ о Лк x_L Лкd-T - r- J x [1 2Лк+1 r2 + Лк+2 r4] dx r2 Стоящее в правой части этого неравенства выражение равно нулю. Это можно проверить непосредственным подсчетом. Из этого значения и из (11) при 0 < r < 1 получим dk(r) > 0, Л2dk(r) > 0, к = 1,2,3,... Из (4) и из (14), (16) заключаем, что при 0 < r < 1, ak(r) > 0, ^k(r) = A2ak(r) > 0, k = 1, 2, 3,... Неравенства (17) и (3) означают, что последовательность {ak(r)}^° неотрицательна и выпукла при 0 < r < 1. Теперь докажем, что ak (r) ^ 0. ak(r) Ak ^^^^^^^^r r j w(x)xk-1 dx + r-2kw(r)rk-1 + ш(г)гk 1 2k-1 2kr ^^^^^^^^r 1 Ak r j w(x)xk-1dx + 2w(r)r-k-1 Так как w(x) — неубывающая функция на [0,1), то J^ w(x)xk-1dx ^ ^(rk r . Следовательно, ak(r) не возрастает. Это означает, что справедливость неравенства (1) вытекает из известной теоремы о неотрицательных тригонометрических рядах (см. [10, с. 100]). Этим и завершается доказательство леммы. > Имея ввиду представление Аш (z; Z), докажем следующую теорему. Теорема 1. Пусть ш(х) — неубывающая дифференцируемая функция из класса Qo- Тогда A(z; Z)| < exp < (A| -1)/ ^ |ζ| dx | A1 (z; Z)| • <1 Из определения Аш (z; Z) имеем A (z; Z )1 I A1(z; Z )| ( 1 - z) e W ■toC) (1 - z) e-Wi(z;0 e-W^ (z;Z) e—Wi(z;0 = e|-W^ (z;0+Wi(z;<)| < exp (A| -1)/ ^ |ζ| dx . > Отсюда, согласно Вш(z; {ak}) = {{k Аш(z; {ak}), получим следующую теорему. Теорема 2. Пусть ш(х) — неубывающая дифференцируемая функция из класса Qo и последовательность {ak} удовлетворяет условию (Б-Дж). Тогда 1ВШ(z; {ak})| < exp < (Ai - О g/ |ak| ^(x)—1dx > |B1(z; {ak})|, x |ВШ(ei^; {ak})| ^ exp < (A1 - О g/ |ak | W(x) - 1 , dx x 0 < ^ < 2n. Замечание 1. Из неравенства (19) следует, что |B.(z; {ak})| < |B1(z; {ak})| , ^(x) € Qo.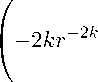
Список литературы Об одной оценке для произведения B М. М. Джрбашяна
- Джрбашян М. М. О параметрическом представлении некоторых общих классов мероморфных функций в единичном круге // Докл. АН СССР.—1964.—Т. 157, № 5,—С. 1024-1027.
- Джрбашян М. М., Захарян В. С. Классы и граничные свойства функций мероморфных в круге.— M.: Наука, 1993.—223 с.
- Nevanlinna R. Einduetige Analytische Funktionen.—Berlin: Springer, 1937.
- Привалов И. И. Граничные свойства аналитических функций.—М.-Ленинград: Гос. изд-во технико-теоретической лит-ры, 1950.—337 с.
- Duren P. L. Theory of Hp Spaces.—N. Y.-London: Academic Press, 1970.—260 p.
- Jerbashian A. M. Functions of a-Bounded Type in the Half-Plane.—Springer Sience+Business Media, ins,—2005. DOI: 10.1007/b102102.
- Захарян В. С., Даллакян Р. В. О граничных значениях функций классов Aш // Докл. НАН Армении.—2012.—Т. 112, № 2.—С. 135-140.
- Захарян В. С., Даллакян Р. В., Джрбашян А. М. Об ^-характеристиках аналитических в единичном круге функций // Докл. НАН Армении.—2013.—Т. 113, № 1.—С. 22-29.
- Даллакян Р. В. О C-росте ^-характеристик аналитических в единичном круге функций // Докл. НАН Армении.—2013.—Т. 113, № 2.—С. 142-149.
- Бари Н. К. Тригонометрические ряды.—М.: Физматгиз, 1951.
- Захарян В. С. Об одной оценке для произведения М. М. Джрбашяна // Изв. АН Арм. ССР.— 1988.—Т. 23, № 2.—С. 189-192.


