Об одной задаче оптимизации формы в стоматологии
Автор: Жолудев С.Е., Кандоба И.Н.
Журнал: Российский журнал биомеханики @journal-biomech
Статья в выпуске: 2 (76) т.21, 2017 года.
Бесплатный доступ
В работе рассматривается одна прикладная задача оптимизации упругой формы. Она возникает в ортопедической стоматологии и содержательно заключается в определении оптимальной формы цельнокерамической реставрации (микропротеза) при восстановлении депульпированного зуба без использования армирующих штифтов. Оптимальной считается та форма микропротеза, которая при заданной внешней статической нагрузке обеспечивает равномерное распределение значений напряжений, возникающих на контактной границе реставрации с зубными тканями. При этом допустимая форма микропротеза должна удовлетворять ряду естественных для этой задачи габаритных, изопериметрических и других ограничений. Основной целью работы является разработка подходов к определению формы микропротеза, близкой к оптимальной (субоптимальной формы). Для этого используются методы математического и численного моделирования. В предположении однородности и изотропности материалов неоднородной конструкции «зуб - микропротез» строится математическая модель задачи. Для определения субоптимальной формы применяется метод последовательных приближений. Задается допустимая начальная форма контактной границы. Затем строится последовательность форм, в которой каждая последующая форма получается из предыдущей при помощи специальной локальной вариации контактной границы. Такая вариация обеспечивает выполнение всех ограничений и уменьшает значение минимизируемого функционала на каждой последующей форме. В результате строится близкая к оптимальной форма контактной границы. Применимость предлагаемого подхода иллюстрируется для случая упрощенной двумерной постановки неоднородной задачи теории упругости, решение которой описывает напряженно-деформированное состояние трехмерной неоднородной конструкции в ее частном плоском сечении. Такая упрощенная постановка возникает в результате применения известного метода плоских сечений. Приводятся результаты математического и численного моделирования.
Неоднородная конструкция, статическая нагрузка, напряженно-деформированное состояние, изопериметрическое ограничение, метод граничных элементов, микропротез, твердые ткани зуба
Короткий адрес: https://sciup.org/146216233
IDR: 146216233 | УДК: 531/534:
Текст научной статьи Об одной задаче оптимизации формы в стоматологии
В настоящее время в стоматологии активно используются результаты математического моделирования процессов, протекающих в такой сложной медикобиологической системе, какой является зубочелюстная система человека. Основные усилия [2, 4, 12, 13, 15] направлены на изучение свойств различных тканей зубочелюстной системы человека на основе разномасштабных математических моделей этой системы. Результатами таких исследований являются в том числе новые практические рекомендации по конструированию протезов, использующихся как для реставрации отдельных зубов, так и для восстановления всего зубного ряда. В клинической практике для этих целей, как правило, применяются протезы, наружная форма конструкции которых ограничивается достаточно жесткими условиями, например, требованиями «окклюзионного компаса» и зубами-антагонистами. В то же время есть основания считать, что вариабельные геометрические свойства формы отдельных элементов некоторых протезов являются одним из факторов, существенно определяющих успех протезирования. Существует мнение, что форма конструкции определенного элемента конкретного протеза является тем ресурсом, за счет рационального использования которого в большинстве случаев можно добиться значительного увеличения жизненного цикла реставрации.
В качестве примера рассмотрим следующую проблему. В стоматологической практике существует методика восстановления зуба при помощи цельнокерамической реставрации (микропротеза), из которой по клиническим показаниям исключены армирующие ее элементы – штифты. Такой подход приводит к необходимости оптимального использования других ресурсов, позволяющих существенно продлить срок службы микропротеза. Одним из таких ресурсов является геометрическая форма вкладки – той части микропротеза, которая контактирует с тканями зуба.
Основной целью работы является разработка подходов к определению формы вкладки, близкой к оптимальной. Для этого используются методы математического и численного моделирования.
Постановка задачи
В большом числе задач биомеханики [3, 12, 13, 14] как зубочелюстная система человека, так и отдельный ее элемент (зуб) может рассматриваться как неоднородная упругая конструкция, подверженная воздействию внешних сил, которые обусловливаются жевательной нагрузкой. Геометрия такой конструкции описывается трехмерной неоднородной областью, представляющей собой объединение конечного числа однородных упругих сегментов, обладающих различными механическими свойствами. К одной части внешней границы области приложена внешняя статическая нагрузка, а другая ее часть жестко закреплена, что соответствует лабораторным условиям проведения эксперимента.
Будем считать, что внешняя граница неоднородной области фиксирована и в ней задано некоторое подмножество, например, зона инфицированного дентина. Производится замена определенной включающей упомянутое подмножество (габаритное ограничение) части неоднородной области дополнительным однородным сегментом (микропротезом) заданного объема (изопериметрическое ограничение). Задача оптимизации заключается в определении формы контактной границы этого дополнительного сегмента с оставшейся частью исходных сегментов, которая бы обеспечивала выполнение указанных выше ограничений и доставляла минимум некоторому функционалу [7–9]. Здесь оптимизируемый функционал характеризует свойства напряженно-деформированного состояния неоднородной области и выражает специфичное требование к оптимальной форме границы. Смысл этого требования заключается в том, что оптимальной формой контактной границы «вкладка – ткани зуба» считается форма, которая обеспечивает на этой границе равномерное распределение напряжений. Это условие отражает лабораторно подтвержденные свойства оптимальной формы контактной границы – чем равномернее на ней распределение значений напряжений, тем потенциально меньше возможность возникновения на ней существенных локальных напряжений, способных привести к разрушению реставрации. При этом указанное выше изопериметрическое ограничение позволяет при протезировании в максимальной степени сохранить здоровые ткани зуба.
Математическая модель задачи
Основой любого метода решения описанной выше задачи оптимизации формы является анализ напряженно-деформированного состояния исследуемой неоднородной конструкции. В полном объеме задача определения напряженно-деформированного состояния такой конструкции может быть решена на базе ее трехмерной геометрической модели. Однако для достижения основной цели работы возможно упрощение этой задачи – допустимо ограничиться исследованием плоской неоднородной задачи теории упругости. Такой подход базируется на общепризнанном экспертами в области сопротивления материалов методе плоских сечений трехмерной конструкции. Кроме того, в силу функциональной специфики зубочелюстной системы человека максимальные напряжения возникают в вертикальных плоских сечениях зуба. Поэтому в дальнейшем ограничимся рассмотрением упрощенной двумерной математической модели задачи оптимизации формы.
Постановка задачи теории упругости
n
Пусть Qc R2: Q = ^rok - односвязная неоднородная область, где гоk -k-I однородные сегменты, упругие свойства которых описываются соответствующими модулями Юнга цk и коэффициентами Пуассона vk (k = 1, 2, .., n) (рис. 1).
К заданной части Г1 внешней границы Г области Q приложены внешние силы Fi (i = 1, 2,..., N), задающие в ее точках ненулевые напряжения f *. В точках другой заданной части Г2 внешней границы Г заданы нулевые перемещения и * = 0 - эта часть границы жестко закреплена. Напряженно-деформированное состояние области Q описывается решением краевой задачи (1)–(4), которая заключается в определении в каждом из составляющих область Q сегментов гоk (k = 1,2,..., n) вектора перемещений и, тензора деформаций £ и тензора напряжений о, которые удовлетворяют в рассматриваемом сегменте системе уравнений о у, i = 0,(1)
£ j = 2 (ил +J
-
о j= 2Ц£ ij+ T2^£ kk 5 ij,
1 - 2v и заданным на внешней границе Г = Г1 иГ2 области Q граничным условиям
-
n у П = fi = fi * на Г 1 ; и , = и , * на Г 2.
Здесь значения всех индексов изменяются от 1 до 2, а по повторяющемуся индексу производится суммирование от 1 до 2, u i j = S u i /5 x j , ц - модуль упругости при сдвиге, v - коэффициент Пуассона, б j - символ Кронекера, n i - вектор нормали к границе сегмента. Значения модуля упругости и коэффициента Пуассона различаются для разных сегментов. На внутренних границах, являющихся границами между сегментами, принимается условие непрерывности перемещений и напряжений.
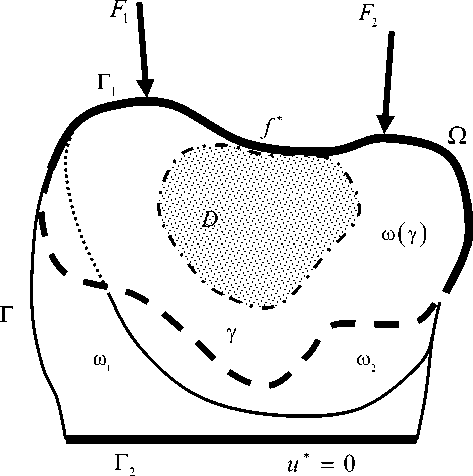
Рис. 1. Неоднородная упругая область, подверженная воздействию внешней статической нагрузки
Постановка задачи оптимизации формы
Зафиксируем односвязное ограниченное замкнутое множество D cQ и величину mes ( D ) < 5 < mes ( Q ) . Пусть часть области Q заменяется (см. рис. 1) односвязным однородным сегментом го ( у ) :
mes (ю(у)) = 5,
D с го(у) c Q, где у - контактная граница сегмента го(у) с сегментами tok (к = 1, 2, .., n).
Обозначим через Ф класс гладких ( С 1) жордановых кривых у c Q , определяющих геометрию контактной границы сегмента to ( y ) . Требуется определить элемент у * е Ф , который бы обеспечивал выполнение условий (5) и (6) и доставлял минимальное значение функционалу
Г2 a z I.
J[r] = f (z(Р)-z (Y)) +1 lМдЧP)) I^P|, Y \ /
Y
где z ( p ) = | f ( p )| - абсолютная величина напряжения в точке p , z ( у ) = ' J z ( p )|ф |, l ( Y ) Y
х » 5z
l(у) - длина кривой у, — - производная напряжения по касательному к кривой у 5т направлению т в соответствующей точке.
Таким образом, задача оптимизации формы сводится к следующей:
min J [ у !
уЕф L J при ограничениях (5) и (6).
Предварительные замечания
Отметим, что вопросы существования и единственности решения в задаче (8) являются крайне нетривиальными математическими проблемами, которые в настоящее время разрешены только для достаточно узких классов подобных задач оптимизации формы, и в данной работе затрагиваться не будут.
Нетрудно видеть, что в задаче (8) достаточным условием оптимальности является тождество z (p) = const.
Х ' p Е у*
Однако, принимая во внимание дополнительные свойства допустимой формы сегмента го ( у ) , обусловленные содержательным смыслом рассматриваемой здесь прикладной задачи оптимизации формы, реализуемость желаемого условия (9) на практике представляется маловероятной. Прежде всего, это обусловливается тем обстоятельством, что не вся граница сегмента го ( у ) является вариабельной - некоторая ее часть принадлежит внешней фиксированной границе области Q , и, как правило, эта часть границы подвержена воздействию заданной внешней статической нагрузки. Более того, в этих условиях ограничения (5) и (6) существенно сужают возможности обеспечить выполнение тождества (9).
По всей видимости, на практике на контактной границе «вкладка – ткани зуба», близкой к оптимальной (субоптимальной) в смысле условия (9), следует ожидать либо кусочно-постоянного распределения значений напряжений без резких изменений их значений с одной константы на другую, либо, что более вероятно, незначительных медленных колебаний значений напряжений вокруг некоторого своего среднего значения. Как представляется, в результате минимизации функционала (7) следует ожидать таких свойств распределения значений напряжений на контактной границе «вкладка – ткани зуба».
Метод последовательных приближений
Для нахождения представляющего практический интерес субоптимального решения в задаче (8) предлагается воспользоваться методом последовательных приближений. Он будет строиться на основе последовательного применения локальных вариаций оптимизируемой границы.
Допустимые в рассматриваемой задаче вариации 5у контактной границы у должны обеспечивать, во-первых, гладкость результата вариации у + 5у и выполнение условий (5) и (6). Требуемую вариацию 5у е R 2 предлагается задавать аналитически
5ye ( p ) = е r ,( p ) n ( p ) , p ey , (10)
где 8 - параметр вариации, 8 > 0; n(p) - единичный вектор внешней нормали к кривой Y в точке p; r. - некоторая заданная на у непрерывная скалярная функция, удовлетворяющая условию j ry( p) |dp| = 0. (11)
Y
Это условие при малых значениях параметра 8 вариации (10) обеспечивает выполнение для сегмента ю ( у + 5у8 ) лишь изопериметрического ограничения (5). Габаритные же ограничения (6) при некоторых не очень жестких дополнительных требованиях к у могут быть удовлетворены за счет выбора в (10) значения параметра 8 .
Существенно более сложной задачей является определение на у такой функции r Y , для которой бы выполнялось условие
3 8(y)> 0: V 0 <8<8(у) ^ J [Y + 5Y8] + aY(8)< J [у],(12)
где aY ( 8 ) :
а„ ( с )
а (е)>0 V 0<8<8(у), а (е)^0, Y v > а > 0.(13)
-
Y 7X7 8^0 8
При построении требуемой функция r Y необходимо учитывать практически все параметры математической модели (1)–(7) задачи (8): геометрические и механические свойства (значения упругих параметров ц k и v k ) образующих неоднородную область Q однородных сегментов го k , особенности локализации и свойства множества D : d способ закрепления и задания статической нагрузки (граничные условия (4)), площадь S и значения упругих параметров дополнительного сегмента го ( у ) .
Здесь, принимая во внимание приведенные выше содержательные аспекты рассматриваемой прикладной задачи, предлагается значения функции rY в точках кривой у вычислять по формуле гД p ) = z (p )-z (y) , p eY. (14)
Такое определение функции r Y базируется на простых инженерных идеях. На тех участках y , где материал «работает» хуже (напряжения меньше величины z ( y ) ), он подрезается с помощью вариации (10), (14). А там, где материал «работает» лучше (напряжения превышают величину z ( y ) ), он добавляется.
Легко проверить, что заданная (14) функция rY удовлетворяет условию (11). Для того чтобы вариация (10) при малых значениях ее параметра 8 обеспечивала в задаче (8) выполнение и габаритного ограничения (6), необходимо начальное приближение Y0 e C2 искомого субоптимального решения y* еФ строить так, чтобы p(Y0,D)>Р0 > 0, где p(y0,D) = mind(p,D), d(p,D) = min|| p —1\|, т.е. расстояние между кривой yо и множеством D должно быть не меньше некоторой величины р0 > 0, зависящей от S в ограничении (5). Тогда, как показывают результаты численного моделирования с использованием реальных данных, удается в задаче (8) с помощью вариации (10), (14) построить сходящуюся последовательность кривых
{ Y k } к =0,1,2,
-
Y k + 1 = y k + 8ye k , 8 k G R, на элементах которой выполняется неравенство
J [ Y к +1 ] < J [ y k ] • Ниже такие последовательности в этой задаче называются аппроксимирующими. При этом проверить выполнение условий (12), (13) для элементов аппроксимирующих последовательностей пока удается лишь экспериментально.
Численное моделирование
Во всех вычислительных экспериментах значения упругих параметров различных тканей зуба (зубная эмаль, дентин) принимались усредненными по известным литературным источникам [5, 14]. В качестве материала реставрации использовалась керамика IPS Empress II. Значения упругих параметров (модуля Юнга ц и коэффициента Пуассона v ) различных материалов приведены в табл. 1.
Таблица 1
Значения упругих параметров
|
Материал |
Коэффициент Пуассона v |
Модуль Юнга ц , МПа |
|
Зубная эмаль |
0,33 |
70 |
|
Дентин |
0,31 |
14,7 |
|
Керамика |
0,28 |
120 |
Исходные предположения
Для построения геометрической модели неоднородной конструкции, описывающей форму плоского сечения восстановленного при помощи цельнокерамической реставрации депульпированного зуба, использовались рентгенограммы (рис. 2).
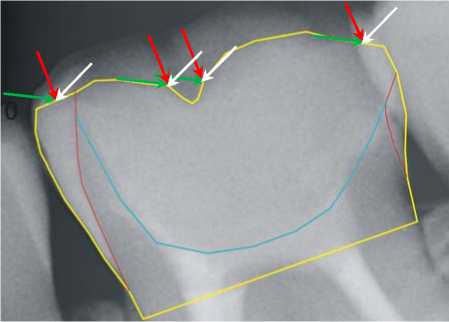
Рис. 2. Геометрическая модель плоского сечения зуба. Возможные направления внешних сил, обусловленные особенностями механизмов функционирования зубочелюстной системы человека
Численное моделирование напряженно-деформированного состояния неоднородной области проводилось при следующих предположениях:
-
а) статическая нагрузка задается набором сил, приложенных к внешней границе зуба, каждая из которых определяется направлением (вектором), величиной и размером площадки приложения;
-
б) плоское сечение зуба жестко закреплено на его нижней части границы (см. рис. 2); игнорируется отдача корней зуба;
-
в) оставшаяся часть границы считается свободной; напряжения в точках этой части границы равны нулю, кроме точек приложения внешних сил; не учитывается взаимодействие исследуемого зуба с соседними зубами;
-
г) все сегменты, соответствующие различным материалам, жестко закреплены друг с другом; при упругой деформации конструкции смещения на контактных границах этих сегментов пренебрежимо малы.
Перечисленные допущения адекватно отражают лабораторные условия проведения эксперимента.
Численное решение задачи теории упругости
Для численного решения задачи теории упругости (1)–(4) применялся хорошо зарекомендовавший себя на практике метод граничных элементов [1]. При этом использовалась методика расчетов, основанная на аналитических вычислениях ряда неизвестных функций [10, 11]. Применение данной методики позволяет во многом избежать традиционных вычислительных трудностей, возникающих при численной реализации операций интегрирования и дифференцирования, необходимых в рассматриваемой задаче для вычисления компонент (касательной и нормальной) напряжений и смещений в точках сечения зуба.
Граничные элементы задавались ребрами ломаных, определяющих границы различных сегментов в геометрической модели плоского сечения зуба. При этом погрешность метода зависит от количества аппроксимирующих границы сегментов граничных элементов, а также от их длин. Метод граничных элементов и аппарат аналитических вычислений позволяют для определения величин компонент напряжений и смещений во всех узлах сечения (средних точках ребер ломаных) построить систему линейных алгебраических уравнений. Кроме того, удается получить аналитические выражения для некоторых характеристик системы, позволяющих определить величины компонент напряжений и смещений в любой внутренней точке неоднородной области.
Пример результатов оптимизации формы
Результаты вычислительных экспериментов показывают, что величина выигрыша от оптимизации формы контактной границы «вкладка – ткани зуба» существенным образом зависит как от параметров математической модели (1)–(5), так и от начального приближения γ 0 указанной границы. В большинстве случаев описанный выше алгоритм позволяет получить достаточно равномерное распределение напряжений на оптимизируемой границе.
На рис. 3 представлен один пример оптимизации контактной границы «вкладка – ткани зуба» в плоском сечении зуба.
На рис. 4 показаны распределения значений напряжений на начальном γ 0 и конечном γ 5 приближениях субоптимальной контактной границы «вкладка – ткани зуба». На рис. 4 по вертикали указываются значения напряжений в точках кривых γ k
( к = { 0, 5 } ). Абсциссы точек этих кривых на рис. 4 последовательно откладываются по горизонтали с использованием относительной величины 100 L натурального параметра l , где L - длина соответствующей кривой у к ( к = { 0,5 } ), l - изменяющаяся от 0 до L длина дуги на кривой у к от начальной до текущей точки.
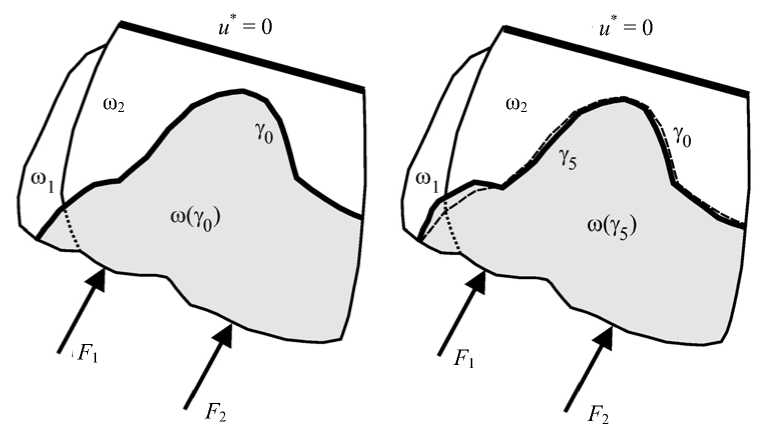
Рис. 3. Результаты оптимизации формы контактной границы «вкладка – ткани зуба»: а - начальная форма (кривая у0); б - конечная форма (кривая у5)
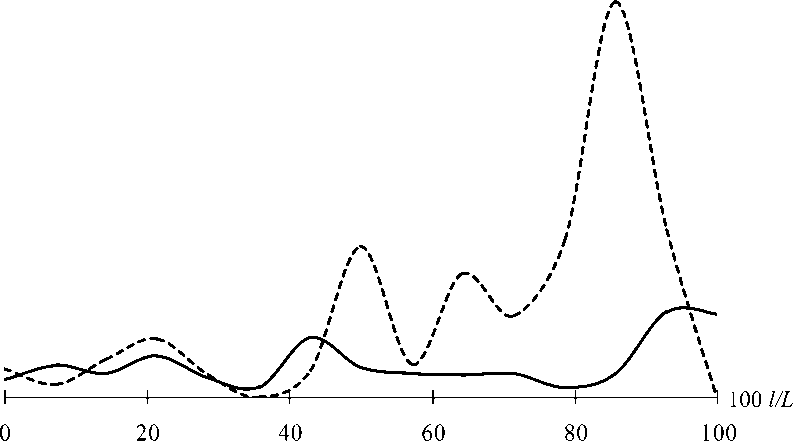
Рис. 4. Распределения значений напряжений z на начальном у 0 (пунктирная линия) и конечном у 5 (сплошная линия) приближениях субоптимальной контактной границы «вкладка – ткани зуба»
В табл. 2 приведена динамика значений количественных показателей, характеризующих степень равномерности распределения значений напряжений на оптимизируемой контактной границе «вкладка – ткани зуба», вычисленных с использованием элементов построенной аппроксимирующей последовательности кривых {Y k } k =0, :
П1: z mn ( y ) = mn z ( P ) ; П2: z max ( y ) = max z ( P ) ; П3: z max ( y )- z mm ( y ) ; П4: z ( y ) ;
( 2 ) 2 1
П5: ll z - z (Y ) L2 = К z ( p )- z (Y ) ) dpp \ ;П6: ( J [y] ) 2 .
Таблица 2
Значения показателей, вычисленных с использованием элементов аппроксимирующей последовательности
|
№ |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
|
0 |
383,374 |
11 400,412 |
11 017,037 |
3 104,697 |
61 145,284 |
62 365,109 |
|
1 |
360,545 |
7 935,178 |
7 574,633 |
2 032,581 |
57 459,973 |
59 273,528 |
|
2 |
511,505 |
5 190,405 |
4 678,899 |
1 864,661 |
35 825,678 |
36 419,027 |
|
3 |
214,971 |
4 514,174 |
4 299,203 |
1 251,372 |
29 365,229 |
30 152,031 |
|
4 |
215,065 |
4 461,159 |
4 246,093 |
1 206,417 |
23 000,454 |
24 316,277 |
|
5 |
254,171 |
2 471,117 |
2 216,94 |
1 030,795 |
17 958,255 |
18 163,091 |
Как видно на рис. 4, в данном примере последовательное применение вариации (10), (14) контактной границы позволяет добиться существенно более равномерного распределения значений напряжений на контактной границе «вкладка – ткани зуба». При этом удается уменьшить разность между максимальным и минимальным значениями напряжения (показатель П3) почти в пять раз, интегральную величину разброса значений напряжений вокруг своего среднего значения (показатель П5) – более чем в три раза, а величину корня квадратного из значения оптимизируемого функционала (7) (показатель П6) – так же, как и значение показателя П5, почти в три с половиной раза.
Численное моделирование проводилось с помощью описанного в [6] пакета прикладных программ (Свидетельство о государственной регистрации программы для ЭВМ № 2011613416 «НДС-ОПТИМА»).
Заключение
Результаты математического и численного моделирования свидетельствуют о применимости предлагаемых подходов к формализации и приближенному численному решению задачи оптимизации формы цельнокерамической реставрации при восстановлении депульпированного зуба без использования армирующих штифтов. Существуют основания считать, что аналогичные результаты могут быть получены и для трехмерного случая.
Список литературы Об одной задаче оптимизации формы в стоматологии
- Бенерджи П., Баттерфилд Р. Методы граничных элементов в прикладных науках. -М.: Мир, 1984. -494 с.
- Делец А.В., Жолудев С.Е., Сапожников С.Б. Обоснование комбинированной шины собственной конструкции с помощью методов математического моделирования//Проблемы стоматологии. -2010. -№ 4.-С. 22-25.
- Деменко В.Ф., Несвит Е.В., Новиков С.С., Шевченко А.А., Третьяк И.Г. Исследование изменения несущей способности коронки зуба при ее контактном нагружении в процессе износа с применением метода конечных элементов//Открытые информационные и компьютерные интегрированные технологии. -2010. -№ 46. -С. 47-68.
- Жолудев С.Е., Кандоба И.Н. Оптимизация формы элемента дугового протеза//Фундаментальные исследования. -2014. -№ 4-2. -С. 274-280.
- Зайцев Д.В., Панфилов П.Е. Прочностные свойства дентина и эмали зубов человека при одноосном сжатии//Вестник Тамбовского университета. Серия: Естественные и технические науки. -2016. -Т. 21, вып. 3. Физика. -С. 802-804.
- Кандоба И.Н., Спевак Л.Ф., Тарико О.С. Анализ напряженно-деформированного состояния в неоднородных конструкциях//Программные продукты и системы. -2012. -№ 1. -С. 69-75.
- Коледа П.А., Жолудев С.Е., Кандоба И.Н. Опыт применения цельнокерамических реставраций на депульпированные зубы//Институт стоматологии. -2007. -Т. 2, № 35. -С. 50-53.
- Наумович С.С., Наумович С.А. Современные возможности и практическое применение математического моделирования в стоматологии//Современная стоматология. -2011. -№ 1. -С. 38-42.
- Тарико О.С., Жолудев С.Е., Кандоба И.Н. Математическое обоснование применения подкладочного слоя в шинирующих дуговых протезах при заболеваниях пародонта, сочетающихся с концевыми дефектами зубного ряда//Уральский медицинский журнал. -2010. -№ 8. -С. 26-28.
- Федотов В.П., Спевак Л.Ф. Аналитическое интегрирование функций влияния для решения задач упругости и теории потенциала методом граничных элементов//Математическое моделирование. -2007. -Т. 19, № 2. -С. 87-104.
- Федотов В.П., Спевак Л.Ф. Модифицированный метод граничных элементов в задачах механики, теплопроводности и диффузии. -Екатеринбург: Изд-во УрО РАН, 2009. -164 с.
- Чуйко А.Н., Шинчуковский И.А. Биомеханика в стоматологии. -Харьков: Форт, 2010. -446 с.
- Чумаченко Е.Н., Арутюнов С.Д., Лебеденко И.Ю. Математическое моделирование напряженно-деформированного состояния зубных рядов. -М., 2003. -261 с.
- Шелковников Е.Ю., Кириллов А.И., Ефремов С.М., Рединова Т.Л., Тимофеев А.А., Метелева Т.Ю. Трехмерное математическое моделирование напряженно-деформированного состояния зуба и пломбы//Ползуновский вестник. -2014. -№ 2. -С. 54-58.
- Kinney J.H., Marshall S.J., Marshall G.W. The mechanical properties of human dentin: a critical review and re-evaluation of the dental literature//Critical Reviews in Oral Biology & Medicine. -2003. -Vol. 14, № 1. -P. 13-29.


