Об одной задаче преследования при наличии сопротивления среды

В работах [1-8] рассматривались различные варианты игровой задачи преследования двух движущихся объектов - перехватчика (преследователя) и цели (убегающего) при следующих предположениях: объекты движутся в некоторой плоскости; оба объекта имеют постоянные по величине скорости и ограниченные значения боковых ускорений; динамика каждого объекта описывается функцией преобразования первого порядка; траектории обоих объектов могут быть линеаризованы при данном геометрическом описании столкновения; доступна полная информация о положении объектов в каждый момент времени.

Одно из решений этой задачи, полученное в [1] и [4], основывалось на ее формализации в виде линейной дифференциальной игры преследования-уклонения с управлениями, принадлежащими компактам. Изначально игра формулировалась в четырехмерном пространстве со следующими координатами: относительное расстояние, относительная скорость и боковые ускорения игроков. Затем с помощью замены переменных игра редуцировалась в скалярную форму и решалась с использованием аппарата теории дифференциальных игр.

В данной статье рассматривается усложненный вариант такой задачи преследования при наличии сил сопротивления среды, пропорциональных квадратам скоростей.

Задача преследования

Постановка задачи

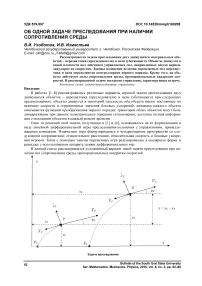
Считаем, что оба материальных объекта ( P – преследователь, E – цель) движутся в одной плоскости (см. рис.). Выберем ось O_x так, чтобы она проходила через начальное положение P ₀ и E 0 объектов P и E . На каждый объект A = P , E действует управляющая сила с_A , перпендикулярная скорости V A объекта, и сила сопротивления среды F A , которая по величине пропорциональна квадрату скорости объекта и направлена в сторону, противоположную его скорости.

Целью преследователя является осуществление захвата цели. Это означает, что расстояние до цели не должно превосходить заданного числа г >  0 .

Запишем уравнения движения. Имеем

;xA = VA cosPa, yа = va sinФа, mAx a = mA (Va cos Фа - фAVA sin Фа ) = - cA sin Фа - kAV2 cos Фа , mAУa = mA (Va sin Фа + фAVA cos Фа ) = cA cos Фа - kAVA sin Фа .

Здесь k_A >  0 - коэффициент сопротивления среды, m A - масса материального объекта. Считаем, что законы изменения величин управляемых сил описываются контроллерами первого порядка

C p = 5 p u - c p q p ,   5 p >  0,   q p >  0, | u | < 1,   с: e = 5 e V - C E q E ,   ^ e >  0,   q E >  0, I v | ^ 1.

Умножим уравнение (1) на cos p _A , а уравнение (2) - на sin p _A и сложим. Получим m A V A =- k A V A ².

Умножим уравнение (1) на - sin p _A , а уравнение (2) - на cos p _A и сложим. Будем иметь ^ф A m A V A = c A .

Решая уравнение (4), находим

V a ( t ) =

V A (0)

V a (0) k A t + 1

_ˆ k_A

, k A = m_A

.

Отсюда, учитывая (5), получим

V (0)                       V (0)

V a (0) k A t + 1 . ~ - ; С л — .

V A (0)        ^A m A

x A =           ; ^cos P a , У а = ;t; A ; ^sin Ф а , Ф а = ^ca

V A ⁽⁰⁾ k A t ^{+ 1}                V A ⁽⁰⁾ k A t ^{+ 1}

Если материальные объекты достаточно массивны, то значения с ˆ _A являются достаточно малыми. Поэтому можно считать, что в процессе движения объектов направления их скоростей мало отклоняются от оси O_x . Тогда cos p _A = 1 и sin p _A = p _A . Отсюда и из предыдущих уравнений получим, что

_    VA (0)          _    VA (0)                  V A (0) k A t + ¹

.

x A =             , y A =               , ^p A = ^CA

V A ^{(0) k}A t ^{+ 1}         V A ^{(0) k}A t ^{+ 1}                  V A ⁽⁰⁾

Из первого уравнения в (6) находим, что xA (t) = xA (0) + J-ln (VA (0) k At +1) при k A > 0 и xA (t) = xA (0) + VA (0) t при k A = 0.     (7)

kA

В начальный момент времени x_E (0) >  x_P (0) (см. рис.). Из формулы (7) можем найти условия, при выполнении которых существует момент времени T >  0, при котором будет выполнено условие x_E ( T ) = x_P (T ).

Если k A > 0 при A = P, E, то требуемый момент времени T > 0 должен являться решением уравнения л \ а

Vp (0) kp t +1)     ,                     it

^{PV P} к _ ( x E (0 ^{) -} x P (0) ) ^k E .     _ ^k E

e ; а

V e (0) k E T + 1                        k p

Если а >  1, то выражение, стоящее в левой части уравнения (8), при T ^ +^ стремится к +^ . Поэтому уравнение (8) имеет в этом случае положительный корень. Если k P = k_E = k >  0, то уравнение (8) имеет положительный корень тогда и только тогда, когда

Математика

VP (0) > VE (0)e(xE (0)-xP (0))k и он равен

• 1         _p( X E (0) - X p (0)) k л

T =e--------------- k VP (0) - Ve (0)e(xE (0)-Xp (0))k

В случае 0 <  a< 1 уравнение (8) не всегда имеет положительный корень.

Если k_P = 0 и k_E >  0, то уравнение для определения момента времени T >  0 принимает вид k e V p (0) T - ln ( V e (0) kET + 1 ) = ( XE (0) - xp (0) ) k E .

Выражение, стоящее в левой части этого уравнения, стремится к +^ при T ^ +^ . Поэтому рассматриваемое уравнение имеет положительный корень.

Если k_P = 0 и k_E = 0, то при V_p (0) >  V_e (0) корень

_T = X e (0) - X p (0) V p (0) - V e (0) .

Далее будем считать, что уравнение (8) имеет положительный корень T . Тогда в этот момент времени T будет осуществлен захват цели, если выполнено неравенство

I y p ( T ) - У е ( T )| < £ .                                     (9)

Сведение задачи к однотипной дифференциальной игре

В работах [9, 10] показано, что задача управления с одномерной целью и заданным моментом окончания с помощью линейной замены переменных может быть сведена к однотипной задаче, для которой в работе [11] построено управление, гарантирующее встречу.

Сделаем замену переменных

Ф i 1 + Ve (0) k-Е T w = y + E^ In---EV ' E kE   1 + Ve (0) kEt

-

Ф р i y_P —x—ln P k_P

1 + V p (0) k_pT

1 + V p (0) k_pt

.

Тогда w(T ) = y_E (T ) - y_P (T ) и, как следует из второго и третьего уравнения (6), ^w = -У р ( t ) с р ⁺ ^ E ( t ) с E ;                                  ⁽¹⁰⁾

У A ⁽ t ) =

V a (0) k A t + 1 l_n 1 + V a (0) k A T >  0

A = P , E .

V a (0) k a     1 + V a (0) k A t

Введем новую переменную

TT z = w - <3 _P j e q ^{P (} t ^- r ) y _P ( r ) dr + <3 _E j e q ^{E (} t ^- r ) y _E ( r ) dr .

tt

Тогда z ( T ) = y_E (T ) - y_P ( T ) и, согласно (3) и (10),

5 t5 z = -a(t)u + b(t)v, u e[-1,1], ve [-1,1]; a(t) = —— [eqP(t-r)yP(r)dr, b(t) = ——feqE(t-r)yE (r)dr. mP tm

В работе [11] показано, что, если выполнено неравенство

(a         T.T„ max z(0) + j (b(r)-a(r))dr; max j (b(r)-a(r))dr < £,(12)

V 0              0< t < Tt то в дифференциальной игре (11) управление u (t, z) = sign z обеспечивает в момент времени T выполнение неравенства | z(T) |< £ при любом допустимом управлении | v |< 1. Если же неравенство (12) не выполнено, то управление v(t, z) = signz гарантирует выполнение неравенства | z(T) |> £ при любом допустимом управлении | u |< 1.

Таким образом, если выполнено неравенство (12), то управление преследователя u ( t , z ) = sign z обеспечивает в момент времени T выполнение неравенства (9) при любом допустимом управлении | v | < 1 цели. Поэтому будет осуществлен захват цели в момент времени T .