Об одной задаче типа Дирихле для уравнения составного типа

1. Постановка задачи. В данной работе рассматривается задача типа Дирихле для линейного уравнения третьего порядка составного типа

( д дд

Mu = а- + p— I ( u xx + u yy ) + Lu = g ( x , y ), ^ д x     д y )

где а, в - заданные постоянные, причем а2 + в2 * 0, а L - линейное дифференциальное вы ражение вида

^Lu = a ⁽ x , y ) u xx ^{+ 2} b ⁽ x , y ) u xy ⁺ c ⁽ x , y ) u yy ⁺ d ⁽ x , y ) u x ⁺ e ⁽ x , y ) u y ⁺ f ⁽ x , y ) u .

Пусть Q обозначает односвязную область плоскости (x, y), ограниченную гладким жордановым контуром 7, который обладает такими свойствами: всякая прямая, параллельная характеристике Px — ay = 0, пересекает его в двух точках, прямые Px — ay = c1 и ex — ay = c2 (c1 < c2) имеют с ним единственные общие точки (точки касания) M и N соответственно. Разобьем кривую 7 на две части 71 и 72 следующим образом: 71 = {(x, y) е 7: axn + Pyn > 0}, 72 = 7 \ 71, где xn = cos(n, x), yn = cos(n, y) и n - внешняя нормаль к границе. Для уравнения (1) изучается следующая краевая задача типа Дирихле:

Задача D _ap . Требуется найти функцию u ( x , у ), удовлетворяющую внутри Q уравнению (1) и краевым условиям

∂u u7 = Ф1(.x, у X    ч-7=^2( x, y),                              (2)

д n ²

где ф 1 (x , y ) и ф ₂(x , у ) - заданные функции .

Можно показать, что в задаче D_a p случай ав <  0 при помощи замены независимой переменной t = 1 - т приводится к случаю ав >  0. Поэтому для определенности положим а >  0, в >  0. Введем некоторые необходимые для дальнейшего обозначения и определения.

Пусть C^{k ,} l ( Q ) - класс функций u ( x , у ), непрерывных вместе со своими частными производными порядка д m ⁺ n u ( x , y )/ д x m д yⁿ для всех m = 0,1, ^ k , n = 0,1, ^ l ; где C^k , ⁰( Q ) = C °- ^k ( Q ) = C^k ( Q ). Под классом C ^{( k} - ^ ) ( Q ) понимаются определенные в области Q функции, у которых все частные производные до порядка k существуют и удовлетворяют условию Гельдера с показателем Я , 0 <  X <  1.

Через C ₁ (/⁾2 h ) [ a , b ] обозначим множество функций ф (t ), заданных на отрезке [ a , b ] и таких, что [( t - a )( b - 1 )]^1/2 ^ ( t ) е C ⁽⁰ ’ ^h ) [ a , b ],0 <  h <  1. Если на этом множестве функций ввести норму

II ^ ⁽ t )| h ,1/2 =||V ⁽ t — a ⁾⁽ b — t ) ^ ⁽ t )|| _C h ,

Математика

где ||-| C - норма в пространстве C ⁽ °’ h ) [ a , b ], то полученное нормированное пространство будет банаховым [1].

Определение 1. Под классическим решением задачи D _ae будем понимать функцию u ( x , у )

из класса C (^ ( Q ) n C ³ ( Q ) удовлетворяющую уравнению (1) и условиям (2) в обычном смысле.

Задачу D _ae будем исследовать в пространстве C (^ ( Q ) n C ³ ( Q ) и в этом случае будем требовать выполнении следующих условий:

Условие 1. Коэффициенты уравнения (1) для любых ( x , у ) е Q удовлетворяют условиям

a ( x , у ), b ( x , у ), c ( x , у ) е C 1 ( Q ); d ( x , у ), e ( x , у ) е C ° ( Q ); f ( x , у ) е C ° ( Q );

кроме того выполняются неравенства д 2 a (x, у)       д 2 b (x, у)

д ² c ( x , у )        д d ( x , у )

П “ ^c 3 ’ 5

д у ²            д x

^д e ^{( x} ’ у ) <  c ∂ y

2 ^_ c l ’ л л ^_ c д x ²           д x д у

Условие 2. Для любых ( x , у ) eQ и ( ^ , n ) е Q , верны неравенства

1)    a(x,у)^2 + 2b(x,у)П + c(x,у)n2 ^ csCY + П2); 2)    a+ 2b + cvv — d — e + 2 f < — c7 < °.

' xx xy уу x у v I

Условие 3. Заданные функции Ф 1 ( x , у ), ф ₂(x , у ) и g ( x , у ) удовлетворяют условиям

Ф 1 ^(x ’ у ) ^{е C}1^⁽ 5 ), Ф 2 ^(x ’ у ) ^е C^W ^и g ^{( x} ’ у ) ^{е C (U)( Q )}

Здесь и всюду ниже через c j ,( j = 1,...,15) будем обозначать положительные постоянные, конкретные значения которых для наших исследований принципиального значения не имеют.

• 2.    Единственность решения задачи D _a p . Справедлива следующая теорема.

Теорема 1. Пусть выполнены условия 1 и 2. Тогда классическое решение задачи Dae един- ственно.

Доказательство. Предположим, что существуют две функции u1(x, у) и u2(x, у), удовле творяющие условиям задачи (1)-(2). Покажем, что u(x,у) = u1(x,у) — u2(x,у). Доказательство этого факта проведем на основании энергетических тождеств. Умножим уравнения (1) на u (x, у) и проинтегрируем по частям в области Q, имеем

u [0^- + в^-

•Q ( ^д x     ^д у

( u_xx + u_yy ) dxdy + jj uLudxdy = °.

Ω

Преобразуем подынтегральное выражение следующим образом

д , R д Y        А u a- + ву- (uxx + u ) = xx yy L д , «д Y ,    . а— + ву- (uuxx + uu ) — ( дx    ду J         уу u (d (x, у) ux + e (x, у) Uy + f (x, у) u) =1    (du )2 +4^- (eu )2 — 1( dx + еу — 2 f) u 2.

2 L дx        ду     J 2

Применяя формулу Грина к интегралу (3) и учитывая однородные граничные условия, получим

72 j ^{[( a x} « ^{— в} у п ) ^u x ^{+ 2( а} у п ^{+ e} x n ) ^u x ^u y ^{+ ( в} у п ^{— a x} n ) ^u 2 ^] ds ⁺ σ

+ JJ [ a ( x , y ) u x + 2 b ( x , y ) u x u y + c ( x , y ) u y J dxdy - ¹ JJ ( a xx + ² b xy + c yy - d x - e y + ² f ) u ² dxdy = 0

Q                                     ² Q

Так как u (x, y) = 0 на границе области Q, то — = 0 на о, поэтому на границе о области Q ∂s выполняются равенства ux = unxn, uy = unyn. В силу равенств xn = ys, yn = -xs, учитывая однородные граничные условия из выражение (4) имеем

2 J ^u 2 ^{( x} n + y 2 ^{)( a x} n + ^Уп ) ^ds + JJ ⁽ a ⁽ x , y ) u x + ^{2 b (} x , y ) u x u y + c ^{( x} , y ) u ^{2) dxd}y -

O ]                                   Q

9 JJ ⁽ a xx + ^{2 b} xy

² Q

+ c yy - d_x - e_y + 2 f )u ² dxdy = 0.

Отсюда в силу условий теоремы 1 заключаем, что u ( x , у ) = 0 в Q . Теорема доказана.

• 3.    Сведение задачи D _ap к интегральному уравнению. Пусть Q - единичный круг с цен

тром в начале координат. Рассмотрим модельное неоднородное уравнение

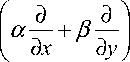
⁽ u xx ⁺ u yy ) = F ^{( x} , У X

с однородными граничными условиями (2). Обозначим через ®(s) неизвестные значения нор мальной производной от искомой функции u (x, y) на о]. Положим aux + Puy = v(x, У X тогда для функции v(x, y) получим следующую задачу Дирихле:

vxx + vyy = F(x, УX v(x, У )0 = ^( sX где д(s) = to(s)(axn + Pyn), если s e о], а д(s) = 0 если s e о2.

Задача Дирихле (7) имеет единственное решение и оно представимо формулой

V (x, У) = J Gn (x, У; s) м( s) ds + JJ G (x, У ;^,n) F (^,n) d^dn,(8)

σΩ здесь G(x,y;^,n) =—ln|(x-^)2 + (y-n)2 I + q(x,y;^,n) — функция Грина задачи Дирихле 2.П уравнения Лапласа. Теперь в области Q решаем задачу aux + Puy = v (x, У), u (x, У )|о2 = 0.

Ее решение можно записать в виде

y

/ х 1 г / а а. л „ ^{u ( x} , У ) = -^     J     ^v ( ^x--:; У ⁺ -j^t , t ) ^dt ,

для

^в Ф( ex-ay )      ^{в в}

где
O : Ф = Ф ( в x - a y ) =---т--- [ ав - 2 a ( e x - a y ) + в а 2 - 4( e x - a y )2 + 4( e x - a y ) ] . 2( а 2 + в 2 ) Подставляя выражение (8) в (9) и меняя порядок интегрирования, получим u ( x , У ) = J k ( x , У ; s ) ^ ( s ) ds + JJ K ( x , y ; ^ , n ) F (^, П ) d ^ d n ,	(10)
здесь , / x 1      y       ( a a x , k ( x , y ; s ) = —     1     G n ( x-—y +— t , t ; s ) dt , в Ф ( Px-ay )        в в	(11)
y K 0 ( x , y ; ^,n ) = — J G ( x-^y + ^ t , t ; ^ , n ) dt P Ф( Px-ay )       P P	(12)

Относительно функции (10) справедливо утверждение.

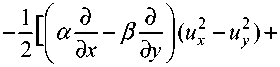
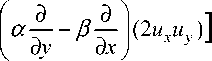
u ( a ( x , у ) u xx

+ 2 b ( x , у ) u„, + c ( x , у ) u_m, ) = — auu_x + buu., xy yy x y

-

2⁽ a x + ^ьу ) u^u

+

∂

+ buu + cuu д у L    x

-

2⁽ b x ^{+ c} y ) u ^{2 —} (■

2 . 2A . ¹ / . . 2 au _r + 2 bu_xu_v + cu _v ) +— ( a_{x r} + 2 b„, + c., ,.) u ; , x x у у' 2' xx xУ уу ⁷

Математика

Лемма 1. Если F ( x , у ) е C ¹¹ h ) ( Q ) и ц (s ) е C^’ 2h ) ( a ), то функция (10) и ее производные непрерывны в области Q , удовлетворяет в классическом смысле уравнению (5) и условию u ( x , у ) = 0 для любой ( x,у ) e c ₂.

Доказательство. Рассмотрим функцию k ( x, у ; s ). Для вычисления интеграла (11) используем формулу.

^д G ⁽ x , у ; s ) =        x ^- У        п( s ) У - П        у s ) + ^д q ^{( x} , У ; ^s )

д п      ( x - У )² + ( у -п )²       ( x - У )² + ( у -П )²            д п

Непосредственно вычисляя значение последнего интеграла найдем ^{k (} x , у ; s ) =      ^в     [ an ^,( s ) ^- ДЛ s ^)] 1п |⁽ x - ^{у )2} + ⁽ у -п )² I + k о ⁽ x , у ; s ),

2( а ² + в ²)

где

_{2 ав}                     2[ a ( x - у ) + ( у - п )]

kо(x, у; s) = ——— [вп,(s)- ау,( s)] arctg —--------- а + в                    (x - У) - в(у-п)

—[ ап '( s ) - вУ ( s )]1п I ( x - ^a у + ^а ф - У )² + ( ф - П )² I - а ² + в ²                   в в

-

2 в

——-г [ ап ( s ) - вУ ( s )]arctg а ² + в ²

а . _ а   а    а р .

2(1 + ^г) Ф + 2(— x --_т у + — У -п )

в ² в  в  в +

⁽ x - ^{у )} - а⁽у -п )

y ∂ q   αα

—( x—у +— t , t ; У , ^J ,д п    в в

Ф( вx-ау )

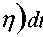
т ₍ х й                                                  д k₀ ( x , у ; s ) д k ₀ ( x , у ; s )

Функция k о ( x , у ; s ) при x = У , у = П непрерывна и ограничена, а --------, --------- ∂ x          ∂ y

непрерывна и ограничена при всех x ^ У , у Ф п , а при x ^ У и у ^ п . Имеет место оценка

дkо(x, у; s) |^ с^ дx         r , дkо( x, у; s) |< С9 ду         r , здесь r2 = (x - У)2 + (у - п)2. Используя равенство

G ( x , у ; У , П ) = 1n I ( x - У )² + ( у - n )² I + q ( x , у ; У , п ), аналогично интегрируются функции K _о( x , у; У , п ):

K о ⁽ x , у ; ^{У ,} П )

в 2 в ⁽x - ^{У )} + ⁽ у - П ) 2    2( а ² + в ²)

1nI( x - У ) + ( у - n )² I + k 1 ( x , у; У , п ),

где

_в 2 в ( x - У ) + ( у - п ) ^k 1 ^{( x} , у ; ^У , ^п )=—^р_{2 2} — 2     ( а ² + в ²)

2[ ^а ( x - У ) + ( у - П )] arctg ——-------------

( x - У ) - а⁽у - п )

-

о 2 ^а ( x - У ) + ( у - П )

— ^в ----5----5----1n I ( x-- у + — Ф - У )² + ( Ф - П )² I

2    2( а ² + в ²)            в ^у в ^{У ) (} ) '

-

o 2 ⁽ x - ^{5 )} - в ⁽ у -П ) ---, ,------arctg

2      ( a ² + в ²)

a ²_x _ a .        a ²      ,

^2[(1 + —^{) Ф +} e ^{( x} - ^{5 )} - в^ У -П ^{] (} x ^{- 5 ) -} в (у -n )

+ у - Ф ( в x — a y ) + —

y

J q (•

Ф ( ex-ay )

αα

. x - в У + ^ t ’ t 5n ) dt ’

и для функции K ₀( x , у; 5 , n ) справедлива оценка

I K 0 ^{( x} , У ; ⁵ - n Ж c w I в ( x - ^{5 + (} y -n ) | In I⁽ x - ^{5 )2} + ⁽ y - n ⁾² I + c l 1 .

Отсюда следует, что функции K ₀( x , у; 5 , n ) непрерывны и ограничены при x = 5 , У = n , а их производные K _{0 x} ( x , у; 5 , n ), K _{0 У} ( x , У; 5n ) непрерывны при всех x Ф 5 , У * n , а при x ^ 5 , у ^ n имеют логарифмическую особенность. Это следует из равенства (12).

Поэтому из теории гармонических потенциалов и условий леммы 1 следует, что функции u ( x , у ) е C ^(1, h ) ( Q ) Q C ³( Q ). Если продифференцировать (10) по x и по у то получим, что u ( x , у ) удовлетворяют уравнению (5). Лемма доказана.

Будем искать решение изучаемой задачи D _aв в виде

u ^{( x} , у ) =    J { тт ^ ^г ^{[ a} n ^{,( s} ) ^{- 5 s )]} In I^{( x - 5 ( s ))2 + (} У ^- n ^{( s ))2} I ⁺ k 0 ^{( x} , У ' ^s ) } Я ^s ) ^ds +

2 п ^ 2( a ² + в Я

⁺Jf ^{{[ a ( x - 5 ) + (} у - n ^)] in I⁽ x - ^{5 )2} + ⁽ у - n ⁾²1 + k 1 ⁽ x , у ; ⁵ , n )^} F ^{( 5 ,} n ) d ⁵ d n ,       ⁽¹³⁾

Ωβ предполагая, что функции д(s) и F(x, у) удовлетворяют условиям леммы 1. Согласно лемме 1, функция (13) удовлетворяет всем условиям задачи, кроме условий u(x,у) ^1 = 0.

В формулу (13) посредством функции д ( s ) входит неизвестная пока функция < у ( s ); для ее определения необходимо перейти к пределу, устремив точки ( x , у ) к точке, лежащей на дуге < 7 1 . Тогда для неизвестной функции го (s ) получим интегральное уравнение первого рода с логарифмической особенностью в ядре

———— J ^{{[ a} n ^{,( s} ) ^{- в5 (s )]in} I ^s 0 ^{- s} I + k 0 ^{( s} 0 , ^{s )}} ® .^{( s} ) ^ds = V ^(s 0 ), 2 n ( a ² + в ²) 7 1

здесь бб* ( s ) = [ an ‘ ( s ) - в5 '( s )] ® ( s );

Я ^s 0 ) = JJ { K ^{( 5 ( s} 0 ) ^{- 5 ) + (} n ^{( s} 0 ) ^- n ^)] In I^{( 5 ( s} 0 ) ^{- 5 )2 +}

Q ^в

^{+ (} n ^{( s} 0 ) ^- n ^{) 2} I^{+ k} 1 ^{( 5 ( s} 0 ), n ^{( s} a ); ⁵ , n )^} F ^{( 5 ,} n ) d ⁵ d n .

Таким образом, решение задачи D _ae для уравнения (5) с однородными граничными условиями эквивалентно решению интегрального уравнения в классе C ₁ ( _/ ⁰ 2 ^ ⁾ ( У 1 ).

• 4.    Разрешимость интегрального уравнения (14). В этом пункте рассмотрим вопрос о существование решения интегрального уравнения (14). Перепишем интегральное уравнение (14), разбив ядро уравнения на регулярную и сингулярную части, в виде

— f in I s 0 - s I ® ^( s ) ds = ^ 1 ( s 0 ), ^{2 n} 0

,              _ x a2 + в2 , x,a2 + в2г,/            d              l где l - длина дуги 71; ^1(s0) =-----—y(s0) +--— k0(s0,s)a*(s)ds. В силу свойств функ-a2          2na2 „

Математика

ции Грина и равенств (11), (12) легко убедиться, что функция k0(s0,s) и ее первые производные являются непрерывными, а у1(s0) - непрерывно дифференцируемая и ^1(s0) удовлетворяет условию Гельдера. Для уравнения (15) справедлива следующая

Лемма 2. Если у 1 ( s ₀) е С ^)^, l ], то единственное решение ю * ( s ) интегрального уравнения

• (15)    существует в классе С ₁ ⁽ °2 ^ ⁾[0, l ].

Доказательство. Дифференцируя (15), получим сингулярное интегральное уравнение

1 l-ю (s) ds'

-I        ds = У1( so),(16)

• ⁿ 0 ^{s - s} 0

общее решение которого имеет вид [2]

• , х 1         1            s ( l - s ) V x , . С

ю<(s0) =--2 / z, x I  ---------У1(s)ds ± / x, п Vs0(l- s0) 0 s s0             Vs0(l- s0)

здесь С - произвольная постоянная. Таким образом, уравнение (16) имеет решение с точностью до произвольной постоянной и для выделения единственного решения надо знать значение интеграла от функции ю*(s) на отрезке [0, l]. Произвольную постоянную С определим таким обра-l зом, чтобы функция (17) удовлетворяла условию J ю*(s)ds = 0. Для этого проинтегрируем (17) на 0

отрезке [0, l ] , получим

\ , х, 1 г ds₀      г V ^{s (} l ^{- s} ) v х, , Vr     ds₀

Ja⁽ , 0 ) d» 0 =- -x J ,      J-^ ^s ) d ± ^С I,     '

0 ^п 0 V ^s 0 ⁽ l ^s 0 ) 0 ^{s s} 0                0 V ^s 0 ⁽ l ^s 0 )

l

Так как J[s0(l -s0)]-1/2 = п, то, изменив порядок интегрирования в интеграле, получим lds

0 ^{( s} 0^{- s} ) 4^{s (} l ^{- s} )

п С = —J Д s ( l - s ) ю ^п 0

Учитывая, что внутренний интеграл в правой части последнего равенства равен нулю, имеем С = 0. Таким образом, согласно условию леммы 2 получаем интегральное вида

ю ( s ₀) + f M ^{( s} , ^{s 0)} ю ( s ) ds = g₂ ( s ₀),                            (18)

0 V s ( l - s )

где ю * ( s ) = V s ( l - s )ж ( s );

M ( s . s 0 ) = ± J V I fL - S ^п 0

∂ s

d S ; g x ( ^s 0 ) =

2( a ² + в²) U- ( l - s ) па ²    0 s - s ₀

у '( s ) ds .

M ( s , s ₀)

Как показано в [2, 3], к интегральному уравнению (18) с ядром . ⁰ - применимы аль-V s ( l 1 - s )

тернативы Фредгольма о разрешимости. После определения функции ю*(s0) решение уравнения (5) удовлетворяющие однородным граничным условиям (2) имеет вид u (x, У) = 2п JJ P (x, У ;!’П) F (!’П) dSdn,                             (19)

где

y

P(x, у ;S,n) = ——-^   J   [G1( x-^- у + ^-t, t ;S,n) - S (x-^y + ^t, t ;S,n)] dt, a2 + в Ф(вх-ay)      в в             в в

Зикиров О.С. Об одной задаче типа Дирихле для уравнения составного типа а S(x,у;^,n) — вполне определенное ядро, зависящее от функции Грина G(x,у;^,n) и ее производных под интегралами; оно является непрерывной функцией вместе с производными любого порядка при (x, у) е Q.

Видно, что функция (19) при любой F ( x , у ) е C ^(1, h ) ( Q ), удовлетворяет уравнению (5) и однородным граничным условиям (2). Теперь подберем F ( x , у ) так, чтобы функция (19) удовлетворяла уравнению (1). Так как функция F ( x , у ) е C ^(1, h ) ( Q ), то производные u_x , u_y , u xx , u_xy , u_yy и

— ( A u ), — ( A u ) существуют и являются непрерывными функциями в области Q , а ∂ x ∂ y

(^7- + вд) (u„ ∂x∂yxx

^{+ U} yy ) = F ^{( x} , у ).

Подставляя (19) в уравнение (1), получим интегральное уравнение

F ( x , у ) =    JJ K ( x , у ; £ П ) F (^, П ) d ^ d n + g ( x , у ),                      (20)

2П Q здесь K(x,у;^,n) = LP(x,у;^,П)• Нетрудно показать, что функция P(x,у;^,n) удовлетворяет не- равенствам

I P ⁽ x , у "Лл ) <  c 12 ^ln I r I; I P x ^{( x} , у; ^ > n ) l < c ³.

I r I

Следовательно, ядро K ( x , у; ^ , n ) не интегрируется с квадратом, но легко видеть [4], что итерированное ядро

K 2 ( x , у ; £ n ) = JJ K ( x , у ; s , t ) K ( s , t ; £ n ) dsdt

Ω интегрируемо с квадратом. Поэтому вместо уравнения (20) рассмотрим интегральное уравнение с итерированным ядром

F ^{( x} , у ) = JJ K 2 ^{( x} , у ; £ П ) g ⁽^, П ) d ^ d n ⁺ g 1 ^{( x} , у ),                         ⁽²¹)

Ω где g1(x,у) = g(x,у) + [fK(x,у;^,n)g(£,n)d^dn. Так как IK(x,у;^,n)I

[3], что IK2(x,у;^,n)I< c₁₅lnr + c₁₆. Следовательно, для уравнения (21) справедливы теоремы Фредгольма. Заметим (см. например [4]), что интегральное уравнение (21) и задача D_ap имеют единственное решение при условии

JJ K2 (x, у; ^, n)dxdyd^dn< 1.

Ω

Решая уравнения (21), находим F(x,у)е C^(1,h)(Э) и тем самым - u(x,у). Проведенные рассуждения доказывают существования классического решение задачи D_ap. Легко проверить, что функция u (x, у) из (19) при любой g(x, у) е C^(1,h)(Э) принадлежит классу C^(1,h)(Q)Q C³(Э). Таким образом, резюмируя изложенное выше, приходим к следующей теореме:

Теорема 2. Пусть наряду с условиями теоремы 1 выполнено и условие 3. Тогда решение задачи D_ap существует. Это решение представимо в виде (9), где функции to(s) и F(x, у) уже известны.

Итак, существование решения задачи D_ap установлено. Заметим, что задачи Коши и Гурса для уравнения 3-го порядка изучались также в [5].