Об одной задаче управления движущейся тележкой с находящимся на ней упругим стержнем

При изучении управляемых процессов колебания упругих систем возникают математические задачи управления гиперболическими уравнениями [1–5]. Так на практике встречаются задачи управления процессом транспортировки упругих балок, когда точное значение внешних сил не известно. При исследовании таких задач можно применить метод оптимизации гарантированного результата [6]. В основе этого метода лежит теория дифференциальных игр [7].

В данной работе рассматривается задача, когда управлением является ограниченное по величине ускорение тележки, на которой лежит упругий стержень. Точное значение величины силы, действующей на стержень, не известно. Известны границы её изменения. Цель процесса управления заключается в том, чтобы в заданный момент времени среднее значение величины растяжения стержня находилось в заданном промежутке. Среднее значение вычисляется с помощью заданной функции. С помощью замены переменной задача сводится к однотипной задаче управления при наличии помехи. Для таких задач, рассматриваемых в рамках теории дифференциальных игр, построены оптимальные управления игроков [8].

Постановка задачи

Рассмотрим тележку, на которой лежит упругий стержень, правый конец которого жестко закреплен, а левый свободен. Трение между стержнем и поверхностью тележки отсутствует. Ускорение w тележки является управлением, и оно ограничено.

При движении тележки стержень совершает продольные колебания. Свяжем с тележкой систему координат, ось X которой направлена по стержню. Считаем, что стержень единичной длины. Плотность совокупности внешних сил, действующих на стержень, задается непрерывной функцией f (x,t), где x - абсцисса некоторого сечения стержня, когда последний находится в покое. Обозначим через U(x,t) смещение этого сечения в момент времени t. Поскольку введенная система отсчета является неинерциальной, то уравнение вынужденных продольных колебаний стержня примет вид [9].

d 2 U ( x , t )     ₉ 5 2 U ( x , t )         _{z х}

----5—- = a2----2   - w+f (x,t),x e [0,1],te [°,P].                    (1) at2

Это уравнение рассматривается при заданных начальных условиях z x       x SU (x,°) z x

U ( x,° ) = g ( x),---1^ = G ( x), где функции g и G непрерывны на отрезке [0, 1]. Кроме того, из условия, что правый конец стержня жестко закреплен, а левый свободен, получим граничные условия [9]

dU(°,t) = °,U(1,t) = °,t е[°,p].(3)

По условию ускорение тележки ограничено, поэтому его можно записать в виде w = ai(t)-a2(t)£, |^< 1, a2(t)>°.(4)

Параметр ξ является управлением.

Считаем, что плотность f (x,t) внешних сил точно не известна. Известна её оценка f2 (x, t )< f (x, t )< fi ( x, t), x е[°,1], t е[°, p ].(5)

Здесь f : [ °,1 ] x [ °, p ] ^ R , i = 1,2 - непрерывные функции.

Заданы числа l е R и 8 > ° . Цель выбора управления $ (4) заключается в том, чтобы осуще- ствить неравенство

J U ( x , p ) а ( x ) dx - l <  8

для любой реализации внешней силы, плотность которой удовлетворяет условию (5). Здесь функция ^ : [ °,1 ]^R является непрерывной и удовлетворяет условиям

а ( ° ) = а ( 1 ) = °.                                       (7)

Формализация задачи

Опишем допустимое правило формирования управления ξ (4). Оно означает, что каждому моменту времени ° <  9 <  p и каждой возможной функции растяжения стержня U ( x, 9 ) ставится в соответствие функция £ : [ 9 , p ] ^ [ °,1 ] . Такое правило будем обозначать

$ ( t ) = ЛГ( t,U ( • , 9 ) ) , t е [ 9 ,р ] .                                      (8)

Зафиксируем разбиение to:° < t° < t1 < "< t; < t;+1 < •< tm+1 = p отрезка [°, p] с диаметром d (ю) = max (t;+1 -1;). Зафиксируем управление (8), плотность f (x,t) °< i < p внешних сил при x е[°,1],° < t < p. Построим решение Uto (x,t),° < x < 1,° < t < p задачи (1)-(3) следующим образом.

Положим g ° ( x ) = g ( x ) , G ° ( x ) = G ( x ) при ° <  x <  1. При t ° <  t <  t 1 ,° <  x <  1 функция U_ю ( x,t ) определяется, как решение следующей задачи:

d ²U „ ( x , t )      2 d 2 U „ ( x , t )      _{z x      z x        z x}

--------= a --------^{+ a}1 ( t )^- a 2 ( t )^i ^{+ f} ( ^x , t ) ,                        ⁽⁹⁾ d t d x

OU,(x, t,-)

U.(x,ti) = gi (x),    »,   ) = Gi(x),(10)

d t

0Um (0, A        ,.

»( , ) = 0, U. (1, t ) = 0,(11)

д x

§i=M( ti, U» (•, ti)).(12)

Здесь i = 0, x e [ 0,1 ] , t e [ t 0 , t 1 ] .

Пусть функция    Uго ( x,t)    определена при    t0 < t < ti-1,0 < x < 1. Положим gi (x ) = U» (x, ti-1), Gi( x ) = 0U. ( x, ti _| )^8t. С помощью формул (9)-(12) строим функцию Uго (x,t) пРи ti-i < t < ti .

Будем говорить, что управление (8) гарантирует выполнение поставленной цели (6), если для любого числа y >e найдется число 5 > 0 такое, что для любого разбиения го с диаметром d (го) <5 и для любой непрерывной функции f (x,t), удовлетворяющей условию (5), выполнено неравенство

J ^U » ( ^x , p ) ⁷ ( ^x ) ^{dx _} l <  Y

Переход к одномерной задаче

Пусть функция у ( х,т ) при 0 < x < 1,0 < т <  p является решением следующей задачи:

^д 2 Ш ( x ^{, т} )    ₂ 5 2 ш ( x ^{, т} )

. 2    = a я 2   , дтдт дш (0,т),

, ) = 0,ш(1,т) = 0,0 < т < p,(15)

° ^ ( x ,2 ) = _{( 7} ( x ) , ш ( x ,0 ) = 0,0 <  x <  1.

Из ра-

Из равенства (7) следует, что условия согласования на концах отрезка выполнены. венств (5) получим, что

J f ( x , t Ш ( x , p _ t ) dx = b 1 ( t ) + b ₂ ( t ) v , |v| <  1.

Здесь b1 (t) = ^J(f1 (x, t) + f 2 (x, t)ш (x, p _ t)dx, b2 (t) = - J(f (x, t)_ f 2 (x, t)У (x, p _ t)dx

20                                            20

> 0.

Положим

• 1    f д ш( x , p _ t)     , x     ,        xd U ^f x , t)

e . ( t ) = J ^ ^') u . ( x , t ) + ш ( x , p _ t )    » ( ' )

Тогда

• / \ г^f д ² ш ( x , p _ t )     ,   .     ,        _xd ² U . ( x , t )^

• ^e . ( t ) = J--^i—- ^U . ( ^x , t ) + ш ( ^x , p ^_ t )—-^—- dx .

6 . ( t ) = J [_ a²

0 1      ^{д т                               d t}     J

Учтем уравнения (9), (14) и равенства (17), (18). Получим

д 2 ш ( x , p  t )

O x ²

U . ( x , t ) dx + J a² ш ( x , p _ t )

J      0 V

д 2 U . ( x , t ) д x ²

^ dx +

J

+ ( a 1 ( t )^_ a 2 ( t ) ^ -) | ш ( x , p ^_ t "dx + b 1 ( t ) + b 2 ( t ) vi-

Ухоботов В.И., Ливанов Н.Д.

при ti< t < ti+1 . Интегрируя по частям и учитывая граничные условия (11) и (15), получим г /       \2 2Um(x, t)     г 8y( x, p -t) 8Um(x, t)     1 d 2^( x, p - A , x

J _V ( x , p - 1 )    ® \ , ) dx - J ^{F( ,P} )    ®® ⁽ , ) dx - f^-1^ u ® ( x , t ) dx.

о               d x ²        Q      d x         d x        ®     dx

Отсюда и из (20) следует, что при t i <  t <  t i + 1

6 ® ( t ) - - Здесь	1 a 2 ( t ) J ^ ( 0	x , p - 1 ) dx		ui + b 2 ( t )’	1 Vi + a 1 ( t ) J ^ ( x , p 0		- t ) + b 1 ( t ) .
Полагаем, что sign 0 - 1. Обозначим Тогда Здесь обозначено	c z ® ( t )- 9 a z ® ( t )-	= - sign p >( t H t - a ( t ) u 1 a 2 ( t )J< 0	1 a 2 ( t ) J ^ ( x V        0 "         1 a 1 ( r ) i ^ ( x , V       0 i + b ( t ) v i , u i		, p - 1 ) dlx I p - r ) dx 1 < 4 v . |s	u . ) + b 1 ( r ) I 1, ti <  t <	dr - 1 . : ti + 1 .	(21) (22) (23)
	a ( t ) -		(	x , p - 1 ^ dx	> 0, b ( t )	- b 2 ( t ) > 0.		(24)

Далее, учитывая условие (11) и формулы (19), (22), перепишем неравенство (13) в следующем виде:

|z ® ( P )| < Y.                                              ⁽²⁵⁾

Условия возможности окончания в одномерной задаче

Рассмотрим одномерную задачу (23), (25). Отметим, что функции (24) являются непрерывными. Построим ломаные tt z® ( t ) = z® ( ti )-J a ( r ) drui + f b ( r ) drVi, ti < t < ti+1,                       (26)

titi с начальным условием z® (0)- z(0). Семейство этих ломаных, определенных на отрезке [0, p], является равномерно ограниченным и равностепенно непрерывным [8, с. 46]. По теореме Арце-ла [10, c. 104] из любой последовательности ломаных (26) можно выделить подпоследовательность, равномерно сходящуюся на отрезке [0, p].

Пусть в (26)

^ui ^- sign ^z ® ( t i ) , i = ⁰, m,                                      ⁽²⁷⁾

а функция z (t) при 0 < t < p является равномерным пределом последовательности ломаных z^^ (t) (26), у которых диаметр разбиения d(®k) ^ 0. Тогда [8, теорема 8.1] выполнено неравен- ство

Здесь обозначено

I z ⁽ p )|< F ⁽ z ^{( 0} ) ) .

[         p_z                                  p_                           ]

F ( z ) = max | z | + j ( b ( r ) - a ( r ) ) dr ; max J ( b ( r ) - a ( r ) ) dr I .

I        0                         ° < r < ^pJ.                         I

Пусть число е > F(z(0)). Тогда можно показать, что для любого числа у > е существует число 5 > 0 такое, что выполняется неравенство (25) для любой ломаной (26) с диаметром разбиения d (to) < 5 и с управлением (27).

Пусть в (26)

v i = sign Z to ( t i ) , i = 0, m ,                                        (28)

а функция z ( t ) при 0 <  t <  p является равномерным пределом последовательности ломаных z^ ( t ) (26), у которых d ( to k ) ^ 0. Тогда [8, теорема 8.2] выполнено неравенство

Iz(Р )< F(z(0)).

Отсюда можно получить, что если числа е <  у <  F ( z ( 0 ) ) , то существует число 5 >  0 такое, что

I zto(Р )> Y, для любой ломаной zm (t) (26) с диаметром разбиения d (ю) <5 и с vi (28).

Таким образом, можно построить управление (8), которое гарантирует выполнение поставленной цели (13) тогда и только тогда, когда F ( z ( 0 ) ) <  е .

Из формул (21), (27) получим, что

Г          ¹

£ = sign za2 (t) j^ (x, p -1 )dx u.

I        0

Здесь z определяется формулами (19) и (22) с заданной в (22) U₀₎ ( x,t ) на U ( x,t ) .

Пример

Пусть функция

ст (x) = 3па sin (nx) sin I П x I, тогда условие (7) выполнено. Рассмотрим функцию

/         Г n V Г п I Г 3п V Г 3п )

ш(x,т ) = 3cos —x sin a-ат - cos —x sin —ат , v 7 У J J ( 2 ) ( 2 )

которая удовлетворяет уравнению (14) и условиям (15), (16). Подставим функцию  ^(х,т) в формулу (19) при Uro (x,t) = U(x,t). Тогда из (22) следует, что z x   3па z (t )=T

1 j cos 0

^П I Г ^П / А 1тг/ А 7

—x I cos I — a ( p - 1 ) I U ( x , t ) dx +

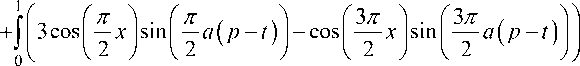
d U ( x , t )

---—-dx + d t

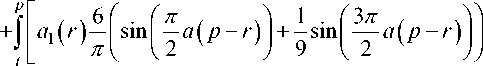
+ b₁ ( r ) dr - 1 .

Алгоритм сведения задачи управления колебанием упругого стержня к одномерной дифференциальной игре разработан В.И. Ухоботовым при поддержке Российского научного фонда (проект 19-11-00105).