Об одном дискретном неравенстве типа Харди с логарифмическим весом

В 1920 г. при попытке упростить неравенства. Гильберта, (см. [20, с. 272]), Г. X. Харди в статье [19] получил неравенство:

∞

p

n =1

p∞ apn, n=1

где p> 1. an > 0 11 An = ^ⁿ₌₁ щ.

Следующее утверждение является аналогом дискретного неравенства. (1) в интегральном случае [20]:

∞

Fp dx xp

∞

/ pV Г

6 |p - 1| f dx

Р> 1 P = 1,

где f (x) — неотрицательная измеримая функция на. [0, то). а x

R ^{f (}f) dt,

P> 1, p <  1.

F (x) = <

∞

R ^{f (}t) dt, x

Константа (p/|p — 1|)p в общем случае не может быть заменена меньшей постоянной. Несмотря на. то, что константа, неулучшаема, не существует функции, на. которой эта. константа, достигается.

Дальнейшие исследования и обобщения неравенств типа. Харди можно найти в работах [2-18, 21-37]. Неравенства, типа. Харди широко распространены, поскольку они

находят широкое применение в математической физике, в анализе и в теории дифференциальных уравнений [1, 5, И, 16, 24]. Например, С. Л. Соболев использовал их в теории вложения функциональных пространств. Ф. Г. Авхадиев [1] использовал неравенства Харди для оценки жесткости кручения. Результаты А. Лаптева, Т. Вейдла из [24], и результаты А. Балинского, А. Лаптева и А. В. Соболева из [И] могут быть применены при изучении отрицательности спектра двумерного оператора Шрёдингера. Другое применение этих результатов относится к проблеме существования резонансных состояний.

Отметим, что в статьях [13, 14, 17, 20, 26] авторы получили дискретные неравенства Харди. Например, в [26] было доказано следующее обобщение неравенства типа Харди:

∞

nα n=1

( Ё aP) n =1

n

p∞α

I 1 n - an, ^^ \2

n=1 х7

где an >  0 (n G N). p >  1 11 —1 < a < p — 1.

Ясно, что дискретные неравенства (1) и (3) при p = 1 и интегральное неравенство (2) при p = 1 теряют смысл. В интегральном неравенстве логарифмический вес помогает устранить эту особенность и позволяет получить аналог неравенства (2) при исключительном случае параметра. Примеры использования логарифмов в неравенствах типа Харди можно увидеть в [2-4, 16, 21, 25, 31, 32]. Приведем лишь результат Ю. А. Дубинского из статьи [16]:

Теорема А. Пусть f : (0, +то) ^ R1 — локально интегрируемая функция такая, что интеграл ∞ j If (r)|prp-1dr,    p > 1, сходится. Тогда для любого R > 0

∞

/ r|ln R|p

r j f (t)dt

R

p dr 6

∞ p

I prp Mr.

Обратим внимание, что в (4) логарифмический вес находится под знаком модуля (см. также [3, 16, 25, 31]). Будут ли верны дискретные аналоги неравенства (4)? В этой работе мы попытаемся ответить на этот вопрос. В первой части этой статьи мы приведем основные и вспомогательные утверждения. Вторая часть посвящена доказательству точности констант. Статьи Ф. Г. Авхадиева и К.-И. Виртца [8-10] также посвящены получению и доказательству точности констант.

2.    Основные результаты

Верна следующая

Теорема 1. Пусть p >  1, l G [1,p], ai > 0 и при целом n >  1 полагаем, что

[R] —1n—

1 6 n 6 [R], n > [R] + 1,

An

Е ai — Е ai, i=0

n

E ai — E ai, i=0

где [R] — целая часть от числа R >  1. Тогда верно следующее неравенство типа Харди:

АП      6 / p \ ¹ X АП ^la^l_n Ilo n Ар

П (n + 1) | log n |^p    Vp ^— V ^ ^{(n +1)1-1}1 ^{og R 1}

1                                                            n 1

Сначала докажем следующее вспомогательное утверждение.

Лемма 2. Пусть p > 1, n Е N, и пусть R — произвольное нецелое положительное число. Если R > n + 1. то и если R < n — 1. to

Р ^{— (}Р ^{— 1)}

⁽ⁿ + 1) (log ^R)

log ПГ Т log^R

)

> 1,

^Р - ^(P - ДС +1) ⁽log R⁾

^log n-^{1 lo}g R

> 1.

<1 Преобразуем неравенство (5). Имеем следующие эквивалентные переходы

1         log -R            1 + (n + 1) log RA p — 1 > (p — 1)

__________+ ^g n +1    ^ ^ 1 >  ^v ' ^g n +1 (n + 1) (log^R) log Ry             (n + 1) log^R

^^ (n + 1) log — > 1 + (n + 1) log----^^ (n + 1) log ^{n +} > 1.

n               n + 1               n

Последнее неравенство легко устанавливается.

Теперь перепишем (6). Имеем

1 >

¹       ₊ ^log ПТ

⁽n ^{+ 1)l}og R log R ‘

После элементарных вычислений можем получить, что

(n + 1) log n > 1 + (n + 1) log n - ¹ ^^ (n + 1) log —n— > 1. R               R              n—1

Последнее утверждение также можно легко показать, в

< ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ. Пусть 1 6 n 6 [R] — 2. Определи!i функцию X следующим образом:

X ⁽ⁿ⁾ =

АП ___p     АП^-1

(n + 1) (^log R )p    p - ¹ (log R )^p-1

A n

A^p            _p      ap ^{- 1}

X ⁽ⁿ⁾ = 7----iTTi— fpvp --T7--- "rAET ^{( А} п - An +1 )

⁽n ^{+ 1)}^og ^R)^{P    p} - ¹(log R)^{p 1}

АП    /     1p ! p    АП-1

⁽log ^RГ¹  (n +1)log R p - ¹ p — ^{1 (}log ^R )^{p - 1 n+1}

p-11

АП   (    1 p V p f   АП           APn+1V .

----------------г I -------------------7T — -------- 1 +--I ------------: 77— I I ~~:------------t^t I log --------. (log R)p-T (n + № R  p — 1 p — 1  (lOg R) (^       log nRi)p

Используя неравенство Гёльдера при соответствующих значениях параметров, мы имеем

X (n) 6

p An

i

(n + 1) log R

-

p

p-

+--

^(log R )

p An

⁽ p ^-1) p

p

-

+

1 A'

p — 1

p- 1

1 A +1        1      Api

- p—1 (log п+Г  p"1 (,og R)p-1

p

-

p —1

(n + 1) log R

-

(p —1)

^{R og} n +1 log R g_n

)

Далее воспользовавшись леммой 1, получаем

X(n)

1 p —1

pp n+1          An

-

/ D \p- 1           R p- 1 ^,

(log n +1)     ^ n

1 6 n 6 [R] — 2.

Очевидно, что X([R]) = 0. Осталось оценить X([R] — 1). Используя вышеприведенные рассуждения и неравенство

16 [R]logiRR—г несложно показать, что x ([R] — 1) 6

1 __ ApR ] - 1

p - ¹ ( ^log T R- 1 )

Далее оценим РП=1 X(n)- Имеем

[ R ]                [ R ]                   p

X X (n) = X ---- n-— £1£1 ^{(n + 1) (lo} g R )

-

p     An ¹

P - ¹ ( log RГ¹

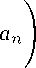
[ R ] - 2

-

p

p

-

-

X

n =1

p

A[R ] - 1

p

An + 1

p- 1

p An

p- 1

-

R\p-1

-

Ap

P — 1(log R)^p-1

6 0.

Следовательно, P^RL X(n) 6 0. Таким образом, справедливо неравенство

[ R ]

X n=1

p An

^{(n + 1)} ( log R ) ^p

6 p

p

-

[ R ]

1X n=1

p- 1 A_n

R yp-1 an‘

Пусть теперь n >  [R] + 3. Определи!i (руикцию Y следутотщш образом:

Y (n) =

p An

(n + 1) (log R)p

-

p An ¹

a.

P ^{— 1} ( log R ) ^p-1

An pp- npn

Y ⁽ⁿ⁾=(n + 1) ( log R ) ^p - p - 1 ( log R Г¹ (An - An^

An    /     1p \ + p    An-1A

( log R ) ^{p—1 (n} + ^1)log R P ^{- 1} P ^{- 1} ( log R ) ^p—1 n— 1

p

An           1

-

(log R)p—1  (n + 1)log Rp

+

p

p -

p

n

,         _s p ( p^- l)

^(log R ) ^p-1

p - 1 ^p

( An—  !pi n-1

I (log v d     r

В силу неравенства Гёльдера, получим

Y (n) 6

p n

(log R Г¹

1 p

-

(n + 1) ( log R )    p ^{- 1}

₊              AP ,     1       AP,- 1

p(p— 1)              1 — p                     _ p— 1

( log R ) ^p—1 ( log nR¹ ) ^p—1    p ¹ ( ^log “ )

1       An 1         1       An

- p - 1 (log n^)p—1   p - 1 (log R)p—1

p ^{- 1}    - ₍ - з ) ^log n-

(n + 1) log R ^{(     )} log R

В последнем утверждении мы использовали тот факт, что p Е (1,p ] и log nR¹ / log RR < 1. Из леммы 1 следует оценка

Y (n)

6--- p-1

An— 1           Ap

-

( log nRd ) ^p—1     ( log R ) ^p—1

n > [R] + 3.

Теперь оцепим Y([R] + 1) 11 Y([R] + 2). Очевидио. что Y([R] + 1) = 0. Используя нера венство

16 (iRi+3)logiRR-;T'

имеем

Y ([R]+2)

p

1A [ R ]+2

p - ¹ ( log [ R + Г ¹

Следовательно, для фиксированного целого N > [R] + 1, получаем

X Y (n) 6

n =[ R ]+1

- p-

p

A [ R ]+2

1(log И+2) p-1

N

+ X n=[R]+3

p

^An— 1

p n

p ^-1   log nF ^p—1

-

(log R)p—1

)

-

p AN

p ^- plog RF ¹

6 0,

t. e. P N=[R]+1 Y (n) 6 0. Следовательно.

N

X n=[R]+1

Apn

⁽n ⁺ 1) ⁽log R ) ^p

p

p

N

X n=[R]+1

p-n

(log R)p

an.

В итоге из (7) и (8), имеем

N

X n =1

Apn

⁽ⁿ + 1) [ log R i p

p p-

N

X n=1

p-1 An

I log R Г¹

an.

Используя неравенство Гёльдера, получим

N

^X n =1

Apn

^{(n + 1)} Ilog R ^[p

N

6 X n=1

p An

^{(n + 1)} Ilog R ^[p

)

l                   l      p-l l p     An an

p-

1    (n + 1)¹ -

n l-p ^[log R

1 l

N

n =1

Apn

⁽n ^{+ 1) [} log R ^[p

N             l     p - l l

+ _ X^   p 1  An an l ^ \P — 1   (n + 1)1-/ n=1

,    n [l-p log RI

Таким образом,

N

^X n =1

_A p_n

^{(n +} 1) ^[ log R ^[p

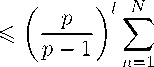
p-l l n an

(n + 1)1-1

n l-p log R1

Устремляя N ^ то. получаем утверзкдепие теоремы. B

Следствие 3. Пусть an >  0 при каждом целом n >  1, p > 1 и

' [R]-1

1 6 n 6 [R], n > [R] + 1,

An

Е ai — Е ai, i=0

n         [ R ] + 1

E ai — E ai, i=0

где [R] — целая часть любо го неотрицательного R > 1. Тогда верно следующее неравен ство типа. Харди

∞

Apn

⁽n ^{+ 1)} Ilog R ^[p

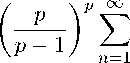
p an

(n + 1)1-p ‘

^X n =1

3.    Точность константы l—p

Пусть an —

0,

( n⁺¹ ) ( log R )

1+ e , ^p

1 6 n 6 [R], n > [R] + 1,

причем p — 1 — e >  0.

Определим Y как

∞

Y — X n =[ R ]+1

p a n

(n + 1)1-p ‘

Прямые вычисления дают

∞

∞

Y = У n=[R] + 1 (n + 1) (log R)

— >

у

.[R +1 (n + 1) (log n +l)

n +1 \ ^1+е

∞

> n=[R]+1

^{(r + 1)} ( log r R ¹ ) ^1+e

∞ dr = / n =[ R ]+1

d log rR¹  = 1

( log rR¹ ) ^1+e" ^e

[R] +2   e log

.

Верно следующее соотношение

Y<--------;-------■

([R] + 2) (log [ RR¹) p

∞

+ 7

n =[ R ]+1

dr.

^{(r +}1) ( log rR¹ ) ⁺

Таким образом,

Y = - (log ε

[R] + 2

R

-ε

+ 0(1).

Также имеем неравенство

n

n

An = E ai = E i =[ R ]+2       i =[ R ]+2

n

>

[ R ]+2

dr

(r + 1) ⁽log rp >  J

^R           [ R ]+2

(i + 1) ( log R ) ^|1+e)/p

n

dr

(r +1) ( logrR¹ ) ^|1+e)/p

p p — 1 — e

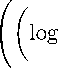
p—1 — E n + 1 \ p

R

-

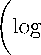
[R] +3

R

p — 1 — E ^p

p

p

—1—e

H (n).

Следовательно,

An      > / p У      H ^p(n)

(n + 1) ( log R ) ^p >  p — 1 — e   (n + 1) ( log nR¹ ) ^p

( p— 1 — E\ p [ R ]+3      P

1 - log j-R- \ p \ __________1__________ log nR1            (n + 1) (log nR1 )1+e

• > 7 p V 1— Kn

p — 1 — e) (n + 1) (log nR! )1+e ’ где Kn ^ 0 nj)ii n ^ to. Таким образом,

∞

X = X n=[R]+1

Apn

(n + 1) ( log R ) ^p

>

p

p

—1

-ε

N

X n =[ R ]+1

1 — Kn

(n + 1) ⁽log nR¹ ) ^1+e

N p                  pN p                 dr              p                   Kn

- p

p

p

—1

-ε

ε

log

[R]+2 R

-ε

+ O(1).

Ясно, что

p

X

Y>

ε

+ еО(1)

Устремляя е ^ 0. полупим

Таким образом, при любом е о > ство

(log [ R J+2)

ε

+ еО(1)

X> p p

Y >  p - 1

.

.

существует an = a_n(E) такое.

что выполнено неравен-

∞

X n =0

p n

p

∞

⁽n ^{+ 1)} Ilog R |^p

>

p an

n =0

(n + 1)1-p ■

Это показывает, что константа неравенства теоремы 1 при l = p является точной.

Автор благодарит своего научного руководителя профессора. Ф. Г. Авхадиева за. ценные советы и замечания.