Об одном эволюционном алгоритме настройки искусственных нейронных сетей

Эволюционные алгоритмы (ЭА) - область вычислительного интеллекта, базирующаяся на идеях биологической эволюции. Среди ЭА выделяют четыре направления: генетические алгоритмы, эволюционное программирование, эволюционные стратегии, генетическое программирование [16]. Они моделируют процесс естественного отбора в популяциях, состоящих из отдельных агентов (особей) посредством применения генетических операторов отбора, мутации и воспроизводства. Для четырех упомянутых направлений существуют различия в представлении, использовании и конкретизации операторов, настройке параметров и др. [16]. В качестве иллюстрации приведем в общем виде схему генетического алгоритма:

Пусть в пространстве поиска х задана функция приспособленности G^X^), требуется найти х* = argmaxG(x) х* = argminG(x)

• V ^{Х 7 ИЛИ}         хеХ         •

• 1.    Случайным образом генерируется начальный конечный набор (называемый популяцией) проб-пых решений ^r (A ’—’Ps )'P,_iS^EA (называемых особями), где 5* - начальный размер популяции.

• 2.    Производится оценка приспособленности текущего поколения, т.е. для каждой особи вычисля

• 3.    Выход, если выполняется критерий останова, иначе - шаг 4.

• 4.    Производится генерация нового поколения посредством применения операторов селекции ^, скрещивания С и мутации М : М -С • S^^k\z^ и переход к пункту 2.

ется значение функции приспособленности:      (A ■•••■A y^i         )

Генетические операторы ^ С _и М _ представляют собой упрощенные аналоги биологических процессов селекции, скрещивания и мутации [18].

Искусственная нейронная сеть (ИНС) является одним из хорошо исследованных методов машинного обучения и представляет собой модель для аппроксимации функций с помощью функций активации, для обучения которой используется какой-либо метод минимизации ошибки на тренировочной выборке.

ИНС можно представить в виде упорядоченного множества обрабатывающих элементов (нейронов), соединенных между собой взвешенными связями. Подобная структура может быть описана ориентированным графом, в котором каждой вершине 1 сопоставлена передаточная функция (функ ция активации) У       4 J , где является выходным сигналом вершины /, j -м вхо дом вершины i, wy - весом, приписанным связи между вершинами z и - порогом (смещением) вершины. Функции J1 обычно выбираются нелинейными (гиперболический тангенс, сигмоидальная функция, функция Гаусса и т.д.).

Процесс решения задач с помощью ИНС включает в себя этап обучения, в процессе которого выполняется определенный алгоритм обучения, когда на вход сети подаются данные, содержащие известные значения выходных переменных, и по результатам сравнения фактических выходных значений с целевыми производится корректировка весов сети, т.е. решается задача минимизации "(г-Жх))²   .

A _м ->m^m, ^е ду - количество примеров в обучающем множестве, i_k - желаемый выходной сигнал для ^ -го примера, f^x_k,W^ - сигнал, выдаваемый сетью для ^ -го примера, W - матрица весов ИНС.

Применение эволюционных алгоритмов для настройки искусственных нейронных сетей. В работах [3-9, 12-17] показано, что перспективным является применение ЭА к обучению ИНС, данная область в зарубежной литературе обозначается как EDNA (Evolutionary Design of Neural Architectures - эволюционное проектирование нейронных архитектур) [4]. При настройке и обучении ИНС эволюционным путем может не только решаться задача поиска весов связей, но также отыскиваться структура сети, параметры избранного алгоритма обучения, обучающая выборка и др. В последние годы одним из наиболее перспективных подходов признается одновременная эволюция весов и структуры нейронной сети, в зарубежной литературе фигурирующая под аббревиатурой TWEANN (Topology and Weight Evolving Artificial Neural Networks - эволюция топологии и весов искусственных нейронных сетей) [5].

При применении эволюционных алгоритмов для решения задачи TWEANN основной проблемой, которая стоит перед исследователем, является проблема кодирования (представления) ИНС, которое в общем случае определяет дальнейший выбор генетических операторов и от которого в большей степени зависит эффективность разрабатываемых алгоритмов [1, 5 ,9].

Оценивать различные представления можно различными способами; подробный набор критериев для оценки различных представлений ИНС включает следующие характеристики: полнота, замкнутость, компактность, масштабируемость, множественность, приспосабливаемость, модульность, избыточность и сложность [4, 9].

Способы кодирования классифицируются как прямые и непрямые. Непрямое кодирование подразумевает хранение информации, общей для ИНС: число и емкость слоев, плотность связей, типы участков для составных сетей и т.д. Это представление отличается большей компактностью и модульностью [4, 5, 9]. Однако в данном способе практически невозможно проследить, какие изменения в генотипе оказались ключевыми и привели изменениям в фенотипе, иными словами - трудно выявить 212

факторы, которые являются положительными для целевой функции адекватности ИНС. Не менее значимыми недостатками являются множество трудностей с подбором генетических операторов, сходимостью и производительностью. Прямое кодирование представляет ИНС в явном виде с указанием всех нейронов, связей и весов, что лишает данный вид представления модульности и увеличивает объемы хранимой информации, однако придает большую алгоритмизируемость и снижает расходы на кодирование/декодирование [12].

В целом можно отметить то, что работы в направлении разработки методик прямого и косвенного кодирования отмечаются как весьма перспективные, и исследования данной предметной области находятся сейчас в самом разгаре [3, 9, 12].

В нашей работе мы станем придерживаться прямого способа кодирования ИНС.

Начальная популяция, как правило, формируется случайным образом. В работах [5, 19] показано, что последовательное усложнение структуры в общем случае эффективней, чем последовательное упрощение, в силу минимизации размерности пространства поиска, поэтому начальная популяция особей должна формироваться из сетей без скрытых нейронов.

В различных работах поднимается вопрос о разрушающем эффекте оператора кроссовера (скрещивания) [1, 5, 14, 15]. Вопрос о характере задач, для которых оператор кроссовера эффективен, остается открытым. Показано, что кроссовер при использовании представления особей в виде битовых строк приводит к рекомбинации коротких подстрок (т.н. строительных блоков - building blocks [6]), и оценка для строки, получаемой в результате подобной операции, оказывается выше средней оценки родителей [14, 15]. Таким образом, кроссовер, как правило, более эффективен в пространствах поиска, где приспособленность особи хорошо соотносится с ее представлением. В случае искусственных нейронных сетей показано [15, 20, 21], что подобное соотношение нарушается в связи с характером самого пространства поиска. Также следует отметить повышение вычислительной трудоемкости для операций кодирования/декодирования. Данная проблема решается различными способами [14].

Алгоритм одновременной настройки весов и структуры нейросети. Будем использовать ЭА для обучения ИНС прямого распространения (без обратных связей). В качестве единственного репродуктивного оператора будем использовать адаптивный оператор мутации, тогда эффективность разрабатываемого алгоритма в основном будет обусловлена представлением особей (способом кодирования ИНС) и механизмами адаптации оператора мутации. Количество входных и выходных нейронов будем считать фиксированным и равным соответственно N, и N_o .

В качестве модели представления будем использовать следующую: каждая ИНС может быть однозначно охарактеризована списком своих связей (с указанием смежных нейронов и значением весового коэффициента) и списком узлов (с указанием входящих и исходящих связей). Отметим, что список узлов, отчасти дублирующий информацию, содержащуюся в списке связей, увеличивает объем памяти, требуемый для хранения информации о каждой ИНС, однако подобная избыточность по памяти доставляет небольшой выигрыш в вычислении выходного сигнала сети и позволяет отслеживать некоторые исторические изменения для каждой сети. Помимо кодирования собственно ИНС, в генотипе каждой особи будем хранить два параметра, характеризующие направление развития особи: direction G {0,1} (направление развития сети: при каждом усложнении принимает значение 1, при упрощении - 0) и age > 0 - возраст сети (количество итераций без структурных изменений).

Ближайшими аналогами подобного представления являются модели, используемые в алгоритмах NEAT [5] и NEvA [17]. В первом случае отличия проявляются в отсутствии исторических меток и наличии информации о связях, во втором - в наличии списка узлов. В обоих случаях также отсутствуют адаптационные характеристики.

Генотипическое представление

Список связей _______________________ ________________ Список узлов

Nt	1	2	3	4	5	6	7	8
Входящ. нейроны	1	2	2	3	3	6	7	7
Исходя щ. нейрины	6	6	7	7	5	7	4	5
Вес	0.18	0.47	0.45	0.79	0.12	0.92	0.64	0.34

Ne	1	2	3	4	5	6	7
Входящ. связи	-	-	-	7	5,8	1,2	3,4, 6
Исходящ. связи	1	2, 3	4. 5	-	-	6	7, 8

Адаптационные характеристики: age, ^Fitness

Фенотипическое представление

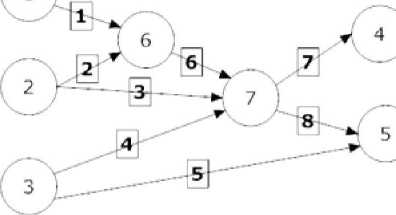
Рис. 1. Представление искусственной нейронной сети в качестве особи для разрабатываемого эволюционного алгоритма

В качестве операторов мутации для ИНС могут быть приняты добавление/удаление нейрона, добавление/удаление связи, изменение весов связей, рекомбинация нейронов/связей [14]. В работе мы станем использовать следующие варианты мутаций:

• 1.    Добавление нейрона. В список нейронов в случайное место вставляется нейрон для всех входящих и скрытых нейронов, расположенных в списке перед вставляемым, разыгрываются с вероятностью pi_an = 0.5 входящие связи со случайным весовым коэффициентом для всех выходных и скрытых нейронов, расположенных в списке после вставляемого - исходящие связи с той же вероятностью.

• 2.    Добавление связи. Для двух случайно выбранных нейронов образуется новая связь.

• 3.    Изменение весов. Для всех связей ИНС с вероятностью применяется оператор Гауссовой мутации - к весам прибавляется случайно выбранное число, полученное с помощью нормального распределения с заданными параметрами.

Для дальнейших выкладок нам потребуются некоторые специфические характеристики ИНС:

• •    Связность С = Ь/Ь^у; , где L - количество связей сети, Ь^щ = Nj * (N₄ 1 ,N_O). + N_H * N_o t ((N_H* Nh ) ^ Nh ) / 2 - максимальное количество связей, N_b N_H. N_o - количество входных, скрытых и выходных нейронов соответственно;

• •    Структурный возраст age = 8_ИегаНо,/Рiteration - отношение количества итераций без структурных изменений данной особи к общему возрасту популяции;

• •    ^Fitness _ приращение фитнесс-функции относительно родительской особи.

Мутации 1-2 относятся к усложняющим структурным мутациям. Очевидно, что вероятность усложнения структуры pSM должна увеличиваться пропорционально в случаях, если структура особи не изменялась продолжительное время Я^' ^ "^ °° и при этом приращение приспособленности относи-„   , ДА —> О „ тельно родительской особи мало: 1    . Во всех остальных случаях - должны изменяться веса особи. При этом ti^' > ^ с количеством итераций, что отражает необходимость тонкой настройки

Psm В а е особей на поздних этапах эволюции:         а^ек               где Psm _ вероятность структур ной мутации, Pwm - вероятность мутации весов свяей, ( ’ ) _ параметры, подбираемые экспериментально. В случае, если структурная мутация происходит, требуется выбрать ее конкретный вид, т.е. решить: добавлять связь или добавлять нейрон. Решение зависит от показателя связности особи, если особь сильно связана - вероятность добавления нейрона будет выше, если особь слабо связана - выше будет вероятность добавления связи: РлсШоЗе 1 Разлей* ’ Разз!** В ^к+Р, где //,77 G (0,1)

Схема разработанного алгоритма, таким образом, имеет вид:

• 1.    Генерация начальной популяции Р_о из уникальных особей a, (i=l,..,N) - сетей без скрытых слоев с различными множествами W(i) связей.

• 2.    Оценка приспособленности текущей популяции fitness(P₁), если выполняются условия выхода (средняя приспособленность не изменяется в течение определенного количества итераций или достигнуто максимальное количество итераций) - шаг 7, иначе - шаг 3.

• 3.    Выбор оператора мутации М( ).

• 4.    Применение выбранного оператора мутации с одновременной оценкой полученных особей.

• 5.    Формирование новой популяции Рщ.

• 6.    Переход на шаг 1.

• 7.    Выход.

В ходе шага 4 для каждой особи применяется выбранный для нее оператор мутации, в ходе шага 5 - особь с наилучшей приспособленностью из предыдущей популяции заменяет особь с наихудшей приспособленностью в новой популяции, т.е. реализуется стратегия элитизма [22].

Разработанный алгоритм реализован в виде библиотеки классов на языке C++.

Задача о балансировании шестов. Для тестирования алгоритма станем использовать известную в области адаптивного нейроуправления задачу о балансировании шестов [23], которая применяется для тестирования нейроэволюционных алгоритмов. Существуют различные разновидности рассматриваемой задачи в зависимости от количества шестов, характера воздействия на тележку, пространства движения тележки, наличия данных об угловых скоростях [24]. В работе будем рассматривать следующую постановку задачи: тележка перемещается в одном измерении, несет на борту два шеста различной длины, сила воздействия - непрерывна. Результаты работы разработанного алгоритма будут сравниваться с результатами работы алгоритмов NeVA [17], SANE [23], ESP [23], CMA-ES [25], NEAT[5], Число запусков алгоритма составит 100 с параметрами, указанными в таблице 1.

Таблица 1

______ Некоторые параметры разрабатываемого алгоритма на задаче с двумя маятниками ______

Параметр	Значение
Размер популяции	Случайный в диапазоне от 10 до 200
ВЛ1,а,Р	Случайные для каждого запуска из диапазона (0,1), на протяжении запуска - фиксированы.

Из таблицы 2 видно, что разрабатываемый алгоритм показал себя хуже CMA-ES и NEvA, опередив SANE, ESP и NEAT при чисто случайном подборе параметров Р’ П^-.Р _и размера популяции.

Таблица 2

Результаты сравнения разрабатываемого алгоритма на задаче с двумя маятниками

Алгоритм	Среднее количество попыток	Размер популяции	Число неудач
SANE	12600	200	0
ESP	3800	200	0
NEAT	3578	150	0
Разраб, алгоритм	2651	85,7	0
NeVA	1448,55	18-200	0
CMA-ES	895	3	0

Сосредоточим наши дальнейшие исследования на подборе параметров ^ ^т1’^а’Р и размера популяции. Установим V^{й —} *-*.5,7/— 0 _п0 преющему будем подбирать ^а^Р случайным образом, но по правилу ^{а <} Р

Таблица 3

Результаты сравнения разрабатываемого алгоритма на задаче с двумя маятниками при первоначальной фиксации параметров Z^z 0 ^, ^/? 0, _и раз_мера популяции=50

Алгоритм	Среднее количество попыток	Размер популяции	Число неудач
SANE	12600	200	0
ESP	3800	200	0
NEAT	3578	150	0
Разраб, алгоритм	1722	50	0
NeVA	1448,55	18-200	0
CMA-ES	895	3	0

Устанавливая параметры ^ ^— ' ’^ ^— ’^{а <}  Р , мы придаем большее значение связности и возрасту особи (важно на первоначальном этапе), а фиксируя размер популяции - искусственно ограничиваем количество вычислений целевой функции. Полученный результат подтверждает гипотезу о важности факторов, однако пока не позволяет улучшить показатели по сравнению с алгоритмом NeVA. Следует отметить также, что:

• -    в среднем вычисление целевой функции в алгоритме NeVA «дешевле» в силу возможностей этого алгоритма по снижению размерности особей, поскольку структурно особи разрабатываемого алгоритма в среднем сложнее особей алгоритма NeVA;

• -    CMA-ES не подбирает структуру сети, решая более простую задачу.

Таким образом, можно утверждать, что разрабатываемый алгоритм, уже при минимальной настройке параметров показывающий значительный рост производительности и результат, сравнимый с лучшими существующими алгоритмами, имеет хорошие перспективы развития за счет своих возможностей по более тонкой настройке параметров.

Дальнейшие исследования разработанного алгоритма следует сконцентрировать как на первоначальном подборе, так и на адаптации параметров М^^^’Р _и размера популяции.

Заключение. В работе представлен нейроэволюционный алгоритм, использующий прямое кодирование нейронной сети списками вершин и связей, основным репродуктивным оператором алгоритма является адаптивный оператор мутации. Информация, необходимая для адаптивного подбора параметров мутации хранится отдельно для каждой особи. Приведены результаты тестирования разрабатываемого алгоритма на модельной задаче о балансировании шестов.

Показана перспективность исследований нейроэволюционных алгоритмов без кроссовера в области хранения параметров мутации индивидуально для каждой особи.