Об одном лагранжево-эйлеровом методе расчета нестационарных течений сжимаемых сред

Моделирование нестационарных течений жидкостей и газов в условиях динамических нагрузок, как правило, основывается на системе законов сохранения массы, количества движения и энергии, записанных в виде дифференциальных уравнений в форме Эйлера или Лагранжа. В случае высокоинтенсивных нагрузок в системе могут возникать ударные волны и волны разрежения, и решение системы дифференциальных уравнений в частных производных представляет собой разрывные (ударные волны) или недифференцируемые (волны разрежения) в отдельных точках функции. При построении численного метода используются различные механизмы, позволяющие описывать в том числе разрывные течения: в уравнения вводятся дополнительные члены с искусственной вязкостью [1], применяются специальные формы разностных уравнений [2], используются физические соотношения для разрывных течений [3, 4]. Во всех случаях разрывы заменяются тонким переходным слоем с большими производными газодинамических величин, так называемая дистракция сильных и слабых разрывов. Лагранжевы методы отличаются меньшей дистракцией и позволяют отслеживать контактные границы. При переходе к моделированию дву- и трехмерных течений в Лагранжевых методах возникают проблемы, связанные с сильными деформациями сетки, что может увеличить общую погрешность численного решения. Поэтому представляется целесообразным объединить преимущества лагранжева и эйлерова подходов. Впервые такая идея была высказана В.Ф. Куропатенко в 60-е годы [5]. Другой вариант сочетания лагранжевых и эйлеровых координат в разностном алгоритме реализован в оригинальном методе ≪частиц в ячейках≫ Ф. Харлоу [6]. Метод Харлоу получил развитие в работах [7–10]. Активно развиваются и другие лагранжево-эйлеровы методы, например, [11–14]. Идея Куропатенко изложена в [15], где предложен подход к построению численного метода, когда на первом этапе применяются уравнения в форме Лагранжа, а затем решение переинтерполируется на неподвижную Эйлерову сетку с выполнением всех законов сохранения. Было рассмотрено две модификации – с использованием на первом этапе методов Неймана – Рихтмайера и дивергентного метода Куропатенко. Первая модификация была успешно использована для решения задачи обтекания, а вторая не была доведена до реализации. Дивергентный метод Куропатенко обладает рядом достоинств: отсутствие эмпирических констант, монотонность, минимальная дистракция разрывов, нулевая диссипация энтропии на непрерывных решениях и использование в качестве механизма диссипации энергии на ударных волнах законов сохранения на поверхности сильного разрыва. Еще одним преимуществом предложенного подхода является использование ортогональных сеток, что существенно снижает вычислительную сложность и погрешности при вычислениях нормальных компонентов векторов скорости, а также позволяет более просто реализовать алгоритмы адаптации сетки. Поэтому реализация предложенного метода представляется перспективной и актуальной задачей.

1.    Численный метод

Для описания течений газа система уравнений механики сплошной среды в лагранжевых координатах имеет вид:

dp + pVU = 0, dt (1) -* dU +1 vp = o, dt ρ (2) dE P dr + J vu = 0' (3) где ρ – массовая плотность газа, U^ – скорость, P – давление, E – удельная внутренняя энергия. Система уравнений (1) – (3) замыкается уравнением состояния

P = P ( P,E ). (4)

Численный метод [15] решения системы (1) – (4) предполагает использование ортогональной сетки по пространству, в двумерном случае ячейки которой образуются линиями x i = const, y j = const (i G [0...N], j E [0...M]), как изображено на рис. 1. Каждый шаг по времени разбивается на два этапа: на лагранжевом этапе происходит расчет величин на подвижной сетке, после этого на эйлеровом этапе выполняется перенос найденных параметров на прямоугольную сетку. Рассмотрим каждый из этапов подробнее. Для вычисления промежуточных величин P ₂ ^∗ _{, 5} , U ₂ ^∗ _{, 5} , которые определяются на грани между ячейками O и A, применяются различные уравнения в зависимости от класса рассматриваемого интервала. Если U x,A < U x,O , то в интервале происходит сжатие, и в соответствии с методом Куропатенко для определения предварительных параметров применяются законы сохранения на сильном разрыве:

Ем = u nO , p ? » = P A + W(u n< - u nO) , P O >P n .         (5)

U X, 2 , 5 = U nA  PS > = P O + W №» - U ’nO ) ,  P O <  P n .          (6)

Здесь W – скорость ударной волны, определяемая из уравнений Гюгонио, в которых в качестве состояния вещества перед разрывом берутся параметры из ячейки с

y

“ j + 2

10 B 9

j + 1 11       3,5 8

C 4,5 43 O 12 2,5 A j 12        1,5         7

5 D 6

i i + 1 r

x

Рис. 1. Шаблон разностной схемы меньшим давлением, а скачок скорости на разрыве полагается равным разности скоростей в ячейках |Uxn,A - Uxn,O |. Если же в рассматриваемом интервале Ux,A ≥ Ux,O , то в интервале решение является непрерывным и применяются уравнения

	U ; , 25 = U n 2 , 5 - 2T- ( P A - P O ) ,                         (7) p. _ Pa + P o   T[(a O ) 2 + (a A ) 2 ] , n      n P 2 , 5 =2             4 h        ( U x , A   U x ,O ),                 (8)
где	„n      (a o №.O + (a A )2UnA   .    L n     npn^n,          ,m U x, 2 , 5          (a n ) 2 + (a n ) 2      , h x 2( x A    X O )('Pa + P O )'              (9)

Здесь a – массовая скорость звука:

2 ∂P a   (dV Л.

Аналогично рассчитываются величины U _x ^∗ , P ^∗ в точках 4,5; 5; 6; 9; 10.

Рассмотрим интервал OB. С помощью уравнений (5) – (9), записанных для оси y, могут быть найдены U _y ^∗ , P ^∗ на грани 1,5 и таким же образом на гранях 3,5; 7; 8; 11; 12. После этого находятся предварительные скорости в узлах путем линейной интерполяции скоростей прилежащих граней. Рассмотрим выражения для узла 1 при условии равенства размеров ячеек O , C , D :

1                                          1 .

u;, i = 2 №.« +     ,  u ; , i = 2 (u;, 1 , 5 + u;^ •

Аналогичным образом получаются величины Ux и Uy в узлах 2, 3, 4. Новые координаты узлов рассчитываются по формулам xn+1 = xn + T ., yn+1 = yn +    '■, k = 1,2,3,4.

По координатам рассчитывается площадь ячейки O в момент времени t ^{n +1} :

S 0 +¹ = 2 [x ;* ⁺¹ (y 2* ⁺¹ - y n +1 )+x 2'' ( у П '' - y ;* ⁺¹ )+x n ⁺¹ (y n ⁺¹ - y 2* ⁺¹ )+х 4 ''У" - y 3* ⁺¹ )] •

Из закона сохранения массы находится плотность:

n n+1 n SO

^P O ^p O Qn +1 •

S _O

Значения компонент скорости в момент времени tn+1 находятся с помощью уравнений u’S = ^ + r №,5 - p«) , hx

U ynO ¹ = U no + _: ^P' - P 1",5 ) • h _y

В конце лагранжева этапа рассчитывается внутренняя энергия в момент времени t ^{n +1} . Для этого определяется, претерпела ли ячейка сжатие или растяжение. Если ρ ⁿ _O ⁺¹ ≤ ρ ⁿ _O , то вещество в ячейке разгружается и используется уравнение изэнтропы:

Vo+1

n +1      n

E O  = E O

-

I P ( V,E ) dV.

V O ⁿ

Если же ρ ⁿ _O ⁺¹ > ρ ⁿ _O , то происходит сжатие вещества и определяются разности скоростей

AU x,O = U * 2 , 5 - U X, 4 , 5 , A U y,O = U y, 3 , 5 - U y, 1 , 5 .

В этом случае для расчета внутренней энергии необходимо учесть сжатие и растяжение по осям. Учет сжатия происходит по формуле

E O = E O -        (p* + P ) (U£ + U^) -

² ‘x,O n +1      n n +1 n

2 l^U x,O     ^U x,O) Wx,O ^{+ U} x,O    ^U x, 2 , 5    ^U x,4,5)

- ⁵ y [_2h-^ (^p 35 + P 15 (U yx^ +^U y 1 л) - ₂ та - ^u;o (U no ¹ + U;o - ^u;₃₅ - U y, 15 J •

Здесь

fl,  AU x,0 < 0,    ₅ = Г1, AU y ,0 < 0,

;    [0,  AUx,0 > 0, y 10, AUy,0 > 0, hx,0 = PO (x2 - xn), hy,0 = PO (y3 - у2) •

При AU _x ,0 > 0 или A U y ,0 > 0 учитывается растяжение по этому направлению с помощью формулы

Vn+l n+1

^e o  = E O

-

У P ( V,E ) dV,

V ∗ в которой объем V, при AUx,q > 0 равен vs = vn + ;   №,2,5 - u,*5, hx,O а при AUy O > 0                    т

'             V S = V 5 + Uj;_m - U y, 15 .

h y O

Если AU x, о <  0 и AU y ,q <  0, то растяжения не происходит и в этом случае E Q ⁺¹ = E Q .

Таким образом, после завершения лагранжева этапа определены величины pn+pEn+1,Un+1 для всех ячеек сетки, а также новые координаты узлов xn+1, yn+1, определяющие положения деформированных ячеек. Эйлеров этап состоит в переносе величин с текущей пространственной сетки на новую ортогональную. При этом сетка, на которую осуществляется интерполяция величин, может быть произвольного разбиения, т. е. доступна возможность измельчения сетки в областях интенсивных процессов. В самом простом случае это сетка, которая была до движения узлов на лагранжевом этапе.

Рассмотрим процесс нахождения величин в ячейках новой сетки [16]. В общем случае, одна эйлерова ячейка может содержать части n деформированных лагранжевых ячеек. Определим объемные и массовые концентрации входящих ячеек ak =

A S k

S e ^,

^ k =

P k A S k ρ e S e

Индексами k и e обозначены параметры, относящиеся к лагранжевой и эйлеровой сеткам соответственно. A S k — площадь пересечения k ячейки с эйлеровой ячейкой. Из законов сохранения массы, количества движения и энергии следуют уравнения для определения величин в новой ячейке:

n

Pe = ^akpk, k=1

n

U e = E^ k P k , k =1

E

e

n

= E i k-( k =1

1, ,- E k ⁺ ^ ll^Uk

- 0 e fl²)

Давление P e вычисляется по уравнению состояния (4).

2.    Результаты тестовых расчетов

Для валидации и верификации численного метода и реализующего его численного алгоритма были решены три тестовые задачи: задача о точечном взрыве (задача Седова), задача о взаимодействии ударных волн различной амплитуды, задача об обтекании ступеньки. Рассмотренные в данной работе задачи широко применяются для тестирования расчетных комплексов, предназначенных для моделирования поведения сплошной среды. Так, в задаче Седова проверяются корректность преобразования потенциальной энергии в кинетическую и работа численного метода на сильных ударных волнах. Наличие аналитического решения позволяет адекватно оценить полученные результаты. Решение задачи о взаимодействии двух ударных волн является сильно зависимым от точности описания разрывов и их дистракции. Моделирование течения в области со ступенькой позволяет проверить точность и устойчивость метода при описании высокоскоростных потоков, а также корректный расчет граничных условий.

• I.    Задача о точечном взрыве (задача Седова) в одномерной области

Постановка задачи [16]. В одномерной области 0 <  x <  0,5 находится идеальный газ с показателем адиабаты 7 = 1,4, с параметрами P = 0, U = (0, 0). В начальный момент времени t = 0 в левой ячейке области задается энерговыделение, соответствующее половине полной энергии взрыва Q = 1. Граничные условия - твердые стенки.

Расчеты проводились на равномерной сетке с шагом h = 0, 001. На рис. 2 представлено сравнение распределений плотности и давления в зависимости от координаты на три момента времени, соответствующих точному и численному решениям. Также представлено решение задачи только на лагранжевом этапе метода, что возможно в одномерном случае и позволяет оценить сглаживание профилей после пересчета величин на эйлеровом этапе.

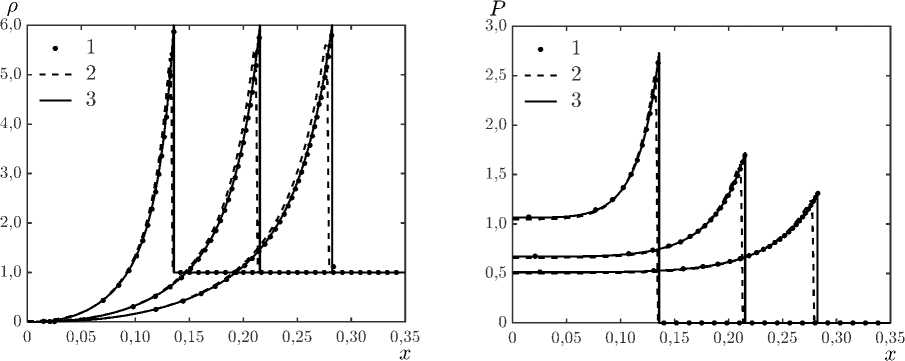
а)                                                   б)

Рис. 2 . Профили плотности а) и давления б) на три момента времени t = 0,05, t = 0,10, t = 0,15; 1 - решение лагранжевым методом, 2 - решение лагранжевоэйлеровым методом, 3 – аналитическое решение

• II.    Задача о точечном взрыве (задача Седова) в двумерной области

Постановка задачи. В двумерной области 0 <  x <  0,1, 0 <  у <  0,1 находится идеальный газ с показателем адиабаты 7 = 1,4, с параметрами P = 0, U = (0, 0). В начальный момент времени t = 0 в четырех центральных ячейках области задается энерговыделение, соответствующее полной энергии взрыва Q = 1. Граничные условия – твердые стенки.

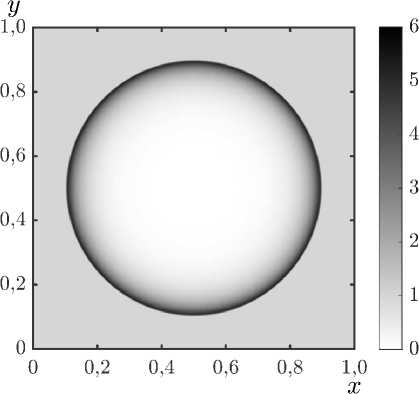
Расчеты проводились на квадратной сетке с шагом h = 0, 001. На рис. 3, 4 представлено сравнение распределений плотности и давления в зависимости от координаты на три момента времени, соответствующих точному и численному решениям. На рис. 4 представлены поля плотности на два момента времени, что позволяет оценить симметричное распространение сферической ударной волны.

• III.    Взаимодействие ударных волн различной амплитуды

Постановка задачи [17]. В одномерной области 0 <  x <  1 находится идеальный газ с 7 = 1,4, который при t = 0 имеет параметры

1000, 0 < x < 0,1, и = (0, 0).

P = 0, 01, 0,1 < 0,9, р = 1, [100,   0,9 < 1,

Граничные условия: все границы – твердые стенки.

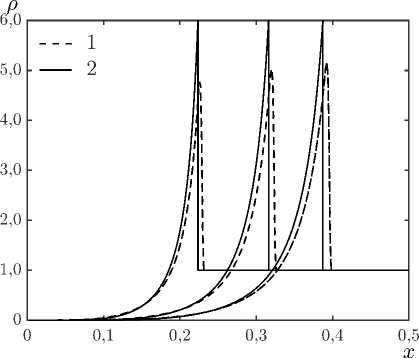
а)

р

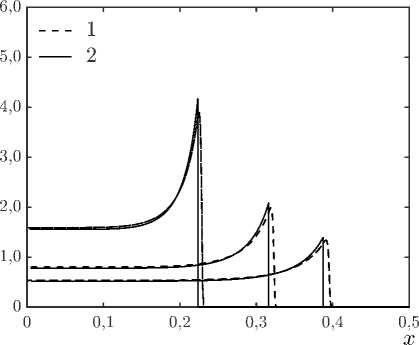
б)

Рис. 3 . Профили плотности а) и давления б) на три момента времени t = 0, 05, t = 0, 10, t = 0, 15; 1 – численное решение, 2 – аналитическое решение

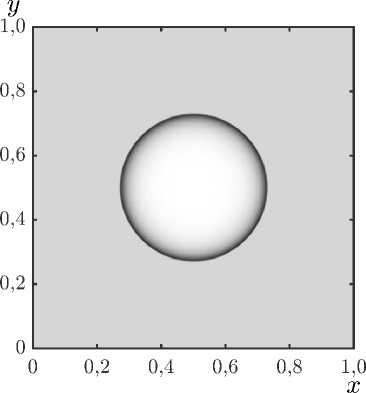
а)

б)

Рис. 4 . Поля плотности на моменты времени a) t = 0, 05, б) t = 0, 15

Расчеты проводились на квадратной сетке с шагом h = 0, 001. На рис. 5 представлена x - t диаграмма плотности. На левом рисунке размещена увеличенная часть диаграммы, содержащая сложную конфигурацию ударных волн и волн разрежения, что позволяет оценить точность описания разрывов.

• IV.    Обтекание ступеньки

Постановка задачи [17]. Рассматривается двумерная область 0 ≤ x ≤ 3, 0 ≤ y ≤ 1 с наличием твердой прямоугольной ступеньки 0,6 ≤ x ≤ 3, 0 ≤ y ≤ 0,2. В момент времени t = 0 область заполнена идеальным газом с параметрами γ = 1,4, ρ = 1, P = 1, U^{^} = (3, 0). Граничные условия: верхняя и нижняя границы – твердые стенки, левая – входной поток с параметрами газа в начальный момент времени, правая – свободное протекание.

Расчеты проводились на прямоугольной сетке с шагами сетки h x = h y = 0, 001. На рис. 6–8 представлены поля плотности на три момента времени, на рис. 9 – поле давления.

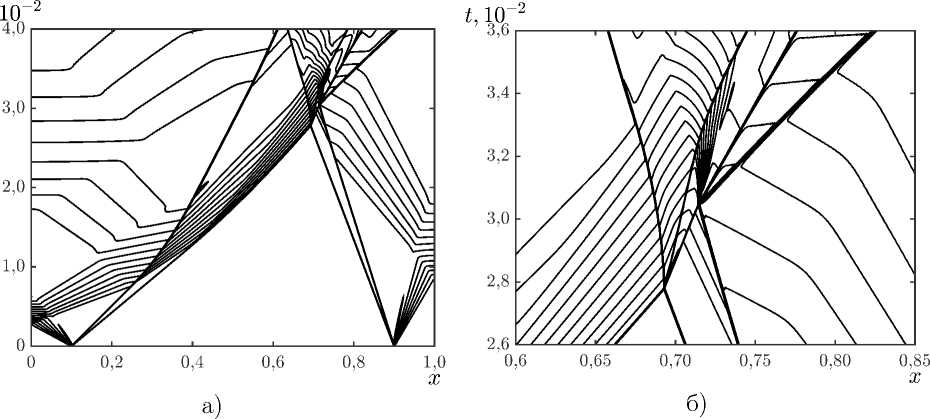
Рис. 5 . Изолинии пространственно-временного распределения ln(p)

Численные расчеты задачи о Седовском взрыве показали близость профилей термодинамических величин к аналитическому решению. Моделирование задач о взаимодействии ударных волн и обтекании ступеньки показали совпадение положений ударных волн, волн разрежения, ножек Маха с эталонным решением.

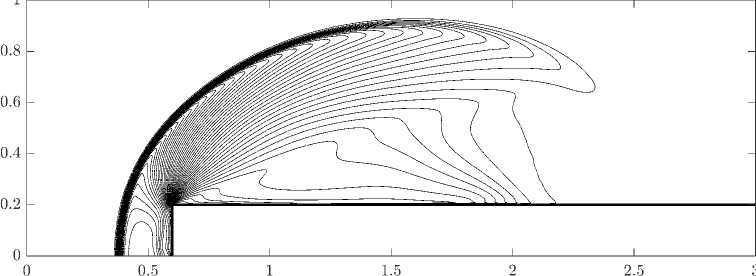
Рис. 6 . Изолинии поля плотности на момент времени t = 0, 5

Заключение

В работе представлена модификация дивергентного метода Куропатенко для одно- и двумерного моделирования поведения сплошной среды в эйлеровых координатах. На лагранжевом этапе метод обладает минимальной дистракцией разрывов и сохранением энтропии на непрерывных решениях. Использование ортогональных сеток существенно снижает алгоритмическую сложность и, соответственно, погрешности, которые непременно возникают из-за использования произвольных сеток.

Результаты тестирования показали высокую точность моделирования течений со сложной структурой взаимодействующих разрывов различных типов – ударных волн и волн разрежения.

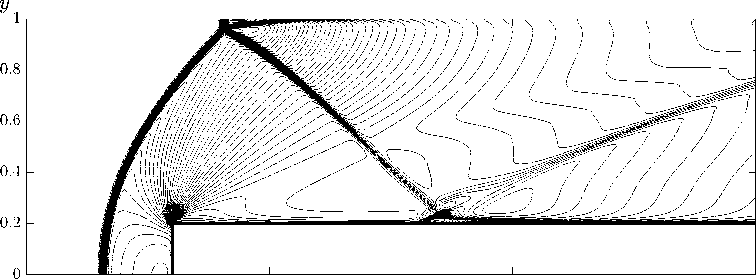
Рис. 7 . Изолинии поля плотности на момент времени t = 2, 0

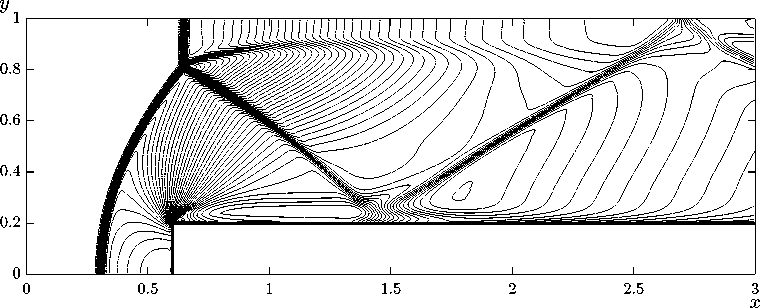
Рис. 8 . Изолинии поля плотности на момент времени t = 4, 0

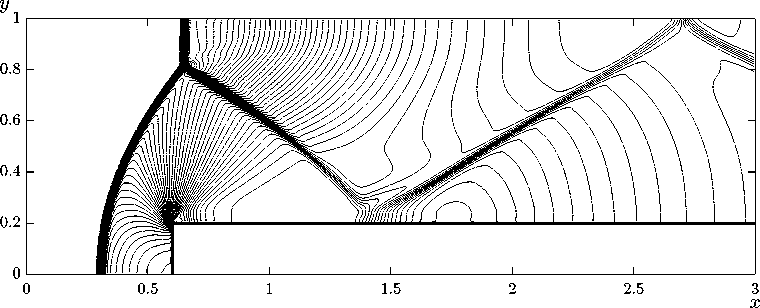
Рис. 9 . Изолинии поля давления на момент времени t = 4, 0

При дальнейшем развитии методики предполагается подключить алгоритм, позволяющий повысить точность численного решения вблизи контактных разрывов, ранее изложенный в [18].