Об одном методе аппроксимации поверхностей уровня функций, заданных на нерегулярных сетках

В работе рассматривается задача интерполяции поверхностей уровня C ² -функций по их значениям в узлах нерегулярных сеток. В статье предложен метод аппроксимации поверхностей уровня, обеспечивающий C ¹ -сходимость без каких-либо ограничений на геометрию узлов сетки.

1.    Метод C1-аппроксимации поверхностей уровня на произвольных сетках

Рассмотрим в области D С R n функцию f (x) класса C 2 (D) такую, что

M 2 = sup max

_D 1 ≤i,j≤n

∂ ² f ∂x _i ∂x j

< + то .

∂f

> °. ∂x _n

Отсюда следует, что найдется постоянная L >  ° такая, что для произвольных точек x ⁰ , x ⁰⁰ ∈ D будет выполнено

V f (x ⁰ ) |V f (x ⁰ ) |

-

V f (x ⁰⁰ )

IV f (x ⁰⁰ ) |

≤ L | x ⁰ - x ⁰⁰ | .

Пусть

m f = i D f ^{f (} x),

M f = sup f (x).

D

Рассмотрим некоторое конечное m f

< c < Mf и некоторую точку x0, f (x0) = c. Соглас но теореме о неявной функции множество уровня Ic = {x Е D : f (x) = c} функции f (x) в некоторой окрестности точки x0 представляет собой график некоторой C1-функции xn = g(x1,..., xn-1). Отметим работы [1; 2], в которых построены оценки размеров областей существования таких функций. Предположим, что найдется постоянная R > ° такая, что для всякого mf < c < Mf и для всякой точки x0 Е Ic найдутся шары B±(R) радиуса R такие, что

B ± n I ^c = x ⁰ , f (x) >  c в B + (R), f (x) <  c в B ^- (R).

Теперь рассмотрим в области D некоторую конечную ε-сеть E, то есть такое конечное множество точек, что для любой точки x ∈ D найдется точка x ⁰ ∈ E такая, что | x — x 0 | < e. Рассмотрим последовательность s-сетей E k с e = 1/k, k = 1, 2,... . Введем дополнительные обозначения

B c = { x : f (x) > c } , A c = { x : f (x) < c } ,

H _k ⁺ (c) = B ^c П E ^k , H-(c) = A c П E ^k .

Выберем некоторые два числа m f < с ₂ < с < с ₁ <  M f и построим поверхность

Г к (c i ,C 2 ) = { x : dist(x, H + (c i )) = dist(x,H - (c 2 )) } ,                 (5)

то есть множество точек, равноудаленных от H ⁺ (с ₁ ) и H ^- (с ₂ ). Эта поверхность, очевидно, представляет собой кусочно-аффинную поверхность, у которой каждая грань представляет собой часть плоскости, проходящей через середину отрезка, один конец которого принадлежит H ⁺ (с ₁ ), другой H - (с ₂ ), и ортогональной этому отрезку. Очевидно, что

Г к (С 1 ,С 2 ) с A c ¹ П B c ² .

Отсюда следует, что

Гк(с1, c2) ^ IС при любом стремлении к ^ то и с1,с2 ^ с. Однако не всегда такая сходимость будет C1-сходимостью. Выясним условия, при которых указанная сходимость будет иметь место. Ясно, что для этого можно ограничиться рассмотрением окрестности точки x0 и соответствующие рассуждения проводить для нормалей к поверхности Гк(с1, с2) и градиентов Vf (x) X IС в соответствии с определением 1. Имеет место следующая лемма.

Лемма 1. Выберем e = 1/к < R . Предположим, что с ₁ ,с ₂ выбраны так, что для точки P _o Е Г _к (с _{1 ?}с ₂ ) и точек P ₁ Е H ⁺ (c ₁ ),P ₂ Е H ^- (с ₂ ) выполнены условия:

| P 0 — P 1 | = | P 0 — P 2 | ,

0, 5R >  | Р о

0,5R > P

— P 1 | =  min P — P ⁰ | = d> 2e,

P 0 eH ⁺ ( c i )

— P 2 I = min P — P ⁰ | = d> 2e, p 0 e H ^- ( c 2 )

d< L .

Тогда имеет место оценка

P 1 — P 2 V f (P o ) | P 1 — P 2 I |V f (P o ) |

< We

- 2

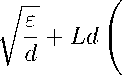
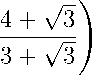
Доказательство. Рассмотрим произвольную точку P ∈ Ic1 . Тогда найдется шар радиуса ε < R, касающийся Ic1 и лежащий в Bc1. Поскольку Ek является ε-сетью, то найдется точка P0 Е H +(c1) (в e окрестности центра указанного шара) такая, что |P — P0| < 2s. Поэтому d < |Po — P0| < |Po — P| + |P — P0| < |Po — P| + 2e.

Таким образом, dist(Po,Ic1) > d — 2е.

Аналогично получаем dist(Po,Ic2) > d — 2е.

Тогда существует шар B (r) с центром в точке P _o и радиусом d — 2е <  r <  d такой, что поверхность I ^{c 1} лежит вне этого шара и касается его сферы в некоторой точке Q ₁ . Согласно предположению найдется шар B + (R), касающийся I c ¹ в точке Q _i , причем эта поверхность лежит вне этого шара. Заметим, что

I c ¹ П B(P o ,d) С B(P o ,d) \ B + (R).

Пусть α1 – значение максимального угла между вектором P0Q1 и вектором P0Q, когда точка Q пробегает множество Ic1 П B(Po,d). Несложно вычислить, что sin ai <

V d² — r ² V (2R — r) ² — d ² 2d(R — r)

В силу условия леммы R > 2d > 2r, d > 2е и по построению d — 2е < r < d, поэтому, после несложных преобразований, получаем sin ai <

3V6 Е

Т" у!

Заметим, что направление вектора P ₀ Q ₁ совпадает с направлением вектора градиента функции V f (Q 1 ), поскольку этот вектор ортогонален I c ¹ в точке Q _i Е I c ¹ . Поэтому из последней оценки приходим к неравенству

P o — Q i V f (Q i ) | P o — Q i l IV f (Q i ) |

.      3V6 E < 2 sin a i <      J                    (7) 2 у d

Аналогично найдем точку Q 2 Е I c ² П B(P _o ,d), для которой

P o — Q i V f (Q 2 ) | P o — Q i l IV f (Q 2 ) |

< 2 sin a 2 <  2 \/|.                  (8)

Применяя неравенство треугольника, получаем

P 1 - P 0 | P 1 - P 0 |

1 ≤ - 2

	P i — P 2     V f (P o ) <  1 2(P i — P o )
+	| P i — P 2 I     IV f (P o ) | <  2 | P i — P 2 I 1 2(P o — P 2 )     V f (Q 2 )     1 V f (Q i ) 2 | P i — P 2 I     |V f(Q 2 ) | ' 2 |V f(Q i ) | 1 V f (Q 2 )     V f (P o ) + 2 |V f(Q 2 ) |    |V f(P o ) | <

V f (Q i ) |V f(Q i )| ^H

_ Vf (P o ) |V f (P o ) l

P i — P o _ V f (Q i )    1 2(P i — P o )

| P i — P o l IV f (Q i ) | ⁺2 | P i — P 2 I

+ 1 P o - P 2 - V f (Q 2 ) + 1

2(P o - P 2 ) _ P o - P 2 | P 1 - P 2 | | P 1 - P 0 |

+ Ld <

+ 2 | P o - P 2 I |V f(Q 2 ) | ⁺ 2

aV6 /7  1

< ""2"" V d ⁺ 2

2 | P i - P o l -      1 2P - P o |

+ Ld.

| P 1 - P 2 I       ⁺2 | P 1 - P 2 I

Применяя геометрические соображения, учитывая неравенство d < L, окончательно получаем

P 1 - P 2    V f (P o ) a V 6 7      (4 + v a !

I P - P 2 I    iv f (P o ) | <  2 Vd ⁺ Ld \a + va) ■

Лемма доказана.

Определим следующую величину

d(c 1 , c ₂ ) = min < inf dist(x,I c ¹ ), inf dist(x,I c ² ) x ∈ I ^c 2                   x ∈ I ^c 1

Ясно, что 5(c 1 ,c 2 ) ^ 0 при c 1 ,c ₂ ^ c. Из леммы непосредственно следует теорема.

Теорема 1. Пусть задана последовательность е сетей E k с е = 1/k . Если c 1 ,c 2 ^ c так, что 5(c 1 ,c 2 ) > V , то Г _к (c 1 ,c 2 ) C ¹ -сходится к I ^c .

2.    Диаграмма Вороного и алгоритм построения линии Гк(с1, c2)

В настоящем параграфе мы раскрываем связь между предложенным выше методом построения поверхностей уровня и хорошо известной конструкцией в вычислительной геометрии — диаграммой Вороного [3]. Мы ограничимся рассмотрением плоского случая. Однако все изложенное ниже легко переносится на многомерные поверхности. Мы предлагаем конструктивное построение ломаной Г _к (с 1 ,с ₂ ) на плоскости.

Напомним определение диаграммы Вороного. Пусть на плоскости задано множество S , содержащее N точек { p i }^. Рассмотрим точку p i . Множество V(i) точек, более близких к p _i , чем к любой другой точке из S , получается в результате пересечения N - 1 полуплоскостей. Это множество — выпуклая многоугольная область, имеющая не более N - 1 сторон. Таким образом,

V(i) = П= H (Pi,Pj), где

H(P i ,P j ) = { x e R ² : | x - P i l < | x - P j |} .

Область V(i) называется многоугольником Вороного, соответствующим точке p i . Получаемые таким образом N множеств образуют разбиение плоскости, представляющее некоторую сеть, называемую диаграммой Вороного Vor(S ).

Пусть задано разбиение множества S на два подмножества S = S 1 U S 2 . Обозначим через a(S 1 ,S ₂ ) множество ребер диаграммы Вороного, общих для пар многоугольников V(i) и V(j) диаграммы Vor(S), где p i e S 1 и p j e S 2 . Совокупность ребер a(S 1 ,S 2 ) называется разделяющей цепью .

Предположим, что зафиксированы c ₂ < c < c ₁ и требуется для заданной ε-сети E построить линию Г _к (c 1 ,c ₂ ). Алгоритм построения этой ломаной линии основан на следующем утверждении.

Теорема 2. Разделяющая линия a(S _i , S ₂ ) диаграммы Вороного Vor(S ) совпадает с искомой ломаной Г _к (c i ,c ₂ ) .

Доказательство. Действительно, точка x Е Гк(ci,c2) согласно определению Гк(ci, c2), если, и только если, выполнено равенство dist(x,H+(ci)) = dist(x,H-(c2)), где расстояния от точки до множества определяется так dist(x, F) = inf |x y∈F

- y | .

Возьмем какое-то ребро L нашей разделяющей цепи a(S 1 , S ₂ ). Тогда найдутся точки p i и p j такие, что:

L = V (p i ) П V (p j ), p i Е H + (c i ), P j Е Н- (c ₂ ).

Рассмотрим произвольную точку x ∈ L. Покажем, что dist(x, H+(ci)) = |x - pil

и dist(x,H-(c2)) = |x - pj |.

Это следует из определения многоугольника Вороного. Действительно, поскольку x ∈ L, то x Е V(pi) и, значит, точка x ближе к точке pi, чем к любой другой точке p Е H+(c1), то есть dist(x, H+(ci)) =   inf |x — y| = |x — pi|.

yeH + ( c i )

Аналогично, поскольку x Е L, то x Е V(pj-) и, значит, точка x ближе к точке pj, чем к любой другой точке p Е Hk-(c2), то есть dist(x,H-(c2)) =   inf |x — y| = |x — pj |.

yeH - ⁽c 2 )

С другой стороны, из того, что x Е V(pi) и x Е V(pj), следует, что dist(x,pi) = = dist(x, pj), а значит, dist(x,H+ (ci)) = dist(x,H-(c2)), то есть x Е Гк(ci,c2). Обратное доказывается аналогично. Теорема доказана.

Теперь алгоритм построения включает в себя следующую последовательность действий:

• 1.    Строим диаграмму Вороного множества точек S = S _i U S ₂ , где

• 2.    Находим разделяющую цепь a(S _i ,S ₂ ), которая в силу теоремы 2 совпадает с r k (c i ,C 2 ).

S i = H + (c i ), S 2 = H - (C 2 )

по одному из алгоритмов, описанных, например, в главе 5 книги [3].