Об одном методе численного решения вырожденных интегро-дифференциальных уравнений со слабой особенностью в ядре

Формулировки многих прикладных задач могут включать в себя дифференциальные уравнения и интегральные уравнения Вольтерра первого и второго рода, а также алгебраические связи. Комбинируя такие уравнения, мы получаем систему интегро-дифференциальных уравнений (ИДУ) с вырожденной матрицей перед главной частью. Такие системы называются вырожденными интегро-дифференциальными уравнениями. Если они не содержат интегральную составляющую, то их называют дифференциальноалгебраическими уравнениями (ДАУ). Если отсутствует слагаемое с производной, то их принято называть интегро-алгебраическими уравнениями (ИАУ), и такие задачи были впервые исследованы в работах [1, 2]. И тот, и другой класс задач достаточно хорошо изучен. В частности, к настоящему времени уже опубликованы сотни статей и десятки моногра- фий, посвященных анализу и численному решению ДАУ (см., например, [3] и приводимую там библиографию). Изучение ИАУ началось несколько позже, чем ДАУ. Впервые их качественные свойства и связь с ДАУ были исследованы в работе [2]. Современное состояние данной тематики частично отражено в работах [4–6]. Среди последних публикаций, посвященных ИАУ со слабой особенностью можно отметить [7, 8]. Однако перенос методов и теории, разработанных для ДАУ и ИАУ на вырожденные системы ИДУ не всегда успешен, поэтому их принято выделять в самостоятельный объект исследования, который к настоящему времени изучен недостаточно, что частично подтверждается списком литературы из недавно опубликованной работы [9], содержащей довольно полный обзор по вырожденным системам ИДУ. Основным принципом исследования таких систем является их расщепление на подсистемы ИДУ и уравнений Вольтерра I и II рода с последующим применением кусочно-полиномиальных методов коллокации. Самым малоизученным классом в данном спектре задач остаются вырожденные системы ИДУ типа Вольтерра со слабой особенностью в ядре, которым и посвящена данная работа. К настоящему моменту сделана только одна публикация по этой тематике [10], которая не содержит численного метода решения.

Системы вырожденных ИДУ имеют важное прикладное значение. Они довольно часто возникают при математическом моделировании различных физических и технических процессов. Примеры моделирования различных динамических систем с помощью вырожденных систем ИДУ могут быть найдены в [11], в частности, к ним могут быть сведены математические модели процессов, протекающих в электрических и гидравлических цепях [12–14]. Вырожденные системы ИДУ даже оказываются полезными при моделировании расположения тазобедренного сустава пассажира, сидящего в кресле автомобиля [15] и во многих других случаях, где необходимо моделирование динамики многотельных систем.

Статья организована следующим образом: во введении описаны задачи, приводящие к появлению интегро-дифференциальных уравнений и приводится обзор литературы по данной тематике. В разделе 1 описывается постановка задачи, раздел 2 посвящен условиям существования единственного решения и содержит необходимые дополнительные сведения. В разделе 4 рассматривается численный метод и анализируется его работа на модельных примерах. В заключении содержится краткая сводка результатов, полученных в работе, с указанием направления дальнейших исследований.

1.    Постановка задачи

Рассмотрим систему интегро-дифференциальных уравнений

t

A(t)x(t) +

B (t)x(t) + j

(t — s) “ K (t, s)x(s)ds = f (t), t E [0,1] = T, 0 < a <  1,

с начальными данными

x(0) = x o ,

где A(t), B(t), K(t, s) — (n x п)-матрицы, f (t) и x(t) — заданная и искомая n-мерные вектор-функции, x0 — заданный вектор из \BbbRn . Предполагается, что все входные данные достаточно гладкие в своих областях определения, и, кроме того, det A(t) = 0 Vt E T.

Такие системы мы называем вырожденными интегро-дифференциальными уравнениями, а под решением начальной задачи (1), (2) будем понимать любую вектор-функцию x(t), которая обращает (1) в тождество и удовлетворяет условию (2). Рассматриваемый класс задач существенно отличается от систем с невырожденной матрицей перед производной искомой вектор-функции. В классической теории, если определитель det A(t) обращается в ноль в изолированных точках отрезка T , то такие точки называются особыми, т.к. решение в них может не существовать или же они являются точками ветвления решений. Однако, если матрица A(t) вырождена на всем отрезке определения, то в этой области решение может оставаться единственным, а может и не существовать.

2.    Существование решения

Приведем ряд известных определений и утверждений.

Определение 1. [22] Пучок постоянных матриц АА + В, А € С называется регулярным, если существует такое А, что det(АA + В ) = 0.

Лемма 1. [22] Пусть пучок постоянных матриц АА + В регулярен. Тогда существуют невырожденные (n х ^-матрицы P и Q с постоянными элементами такие, что

/ E m ⁰

P (АА + B)Q = А I 0 E l

0\ J 0  0

0 I + I 0 M 0

n;   \ 0 0 Ek где m + l + k = n, N,M — нильпотентные матрицы размерностей (k х k) и (l х l) соответственно, Nk1 = 0, Ml1 = 0, k1 < k, 11 < l.

Определение 2. [19] Выражение АA(t) + ^B(t) + C (t), t € T , где A(t), В (t) и C (t) — переменные (n х ^-матрицы, а А, ц — скалярные параметры, будем называть матричным полиномом.

Определение 3. [19] Говорят, что матричный полином АA(t) + ^B(t) + C (t) имеет на отрезке T простую структуру, если выполнены следующие условия:

• 1)    все элементы матриц A(t), В (t) и C (t) принадлежат C m ;

• 2)    rankA(t) = k = const V t € T ;

• 3)    rank(A(t) | B(t)) = k + l = const;

• 4)    det[АA(t) + цВ (t) + C (t)] = a ₀ (t)А ^k Ц + • • • , где a ₀ (t) = 0 Vt € T .

Лемма 2. [19] Пусть матричный полином АA(t) + ^B(t) + C (t) имеет на отрезке T простую структуру. Тогда существуют невырожденные для всех t € T матрицы R(t) и S(t) с элементами из C _T ^m такие, что

R(t)(АA(t) + цB(t) + C (t))S(t) =

E k 0	0	J 1 (t)	0	J 2 (t)	C 1 (t) C 2 (t)      0
А I 0 0	0 I	+ ц I 0	E l	0 I	+ I C 3 (t) C 4 (t)      0
00	0	0	0	0	\ 0      0     E n - k - 1

, t \in T, (5)

где J i (t), J 2 (t), C i (t), C 2 (t), C 3 (t), C 4 (t) — некоторые блоки подходящей размерности.

Определение 4. [20, 21] Псевдообратной матрицей к (m х п)-матрице A(t), t Е T , называется (n х т)-матрица A + (t), удовлетворяющая для любых t Е T уравнениям:

A(t)A + (t)A(t) = A(t),       A + (t)A(t)A + (t) = A(t),

(A(t)A + (t)) ^T = A(t)A + (t),       (A + (t)A(t)) ^T = A + (t)A(t)

Прежде, чем мы сформулируем теорему существования для начальной задачи (1), (2), введем следующие обозначения:

B(t) = (E - A(t)A + (t))B(t),        ^ (t, s) = (E - A(t)A + (t))K(t, s),

C(t) = (E - A(t)A ⁺ (t))f(t),

X«) = dt t (t - s) ^- " (E - B (s) B + (s)K(s)ds. 0

Теорема 1. [10] Пусть задача (1), (2) удовлетворяет условиям:

• 1)    функции A(t), B (t), K (t, s), f (t) дважды непрерывно-дифференцируемы на отрезке T ;

• 2)    (E - A(0)A ⁺ (0))B(O)x o = (E - A(0)A ⁺ (0))C(0);

• 3)    t sin a^(E -S (0) S ⁺ (0)K(0,0)x o = (E - B(0)B + (0))x(0);

• 4)    матричный полином AA(t) + ^B(t) + K (t, t) имеет на отрезке T простую структуру.

Тогда существует единственное непрерывно-дифференцируемое решение задачи (1), (2) на T.

Отметим, что третье условие теоремы обеспечивает совместность начальных данных (2) с правой частью системы (1). Таким образом, теоретически, теорема 1 обеспечивает возможность расщепления системы (1) с помощью серии невырожденных преобразований на три невырожденных подсистемы: систему ИДУ в нормальной форме, систему уравнений Вольтерра первого рода и системы уравнений Вольтерра первого рода. Практически это возможно сделать далеко не всегда. Рассмотрим случай, когда A(t) = 0, и B, K — постоянные матрицы, т.е. система (1) имеет вид:

t

Bx(t) + j (t - s) ^- “ Kx(s)ds = f (t).

Если пучок AB + K регулярен (см. определение 1), то решение системы (6) может быть получено в явной форме. Для этого умножим систему (6) справа на матрицу P и введем замену x = Qy, где P и Q — матрицы из леммы 1. Получим

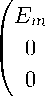
0 0\ /y i (s)\ t J 0 0\ /y i (s)\ /^ i (t) E l 0 I I y 2 (s) I ⁺ / I 0 M 0 I ^{(t -} s^{) -} “ I y 2 (s) I ds = ^ 2 (t) 0 N/ \y 3 (s)/ o \0 0 Ek) \у з (s)/ V3 (t)

где ⁽y ^{T (t),}y ^{T (t),}y ^{T (t)) T} = y^(t), ⁽^ ^{T (t),}^ ^{T (t),}^ ^{T (t)) T} = ^{Pf (t)}. ^Таким образом, исходная система разбилась на 3 подсистемы, для каждой из которых решение можно выписать в явном виде. Первая подсистема представляет собой систему интегральных уравнений Абеля второго рода и ее решение может быть найдено в терминах функции Миттаг-Леффлера [23]:

t

y 1 (t) =

d dt

^ i - _a [Jr(a)(t - s) ¹ " ]0 i (s)ds.

Решение второй подсистемы легко найти, последовательно исключая неизвестные:

y 2 (t) = Ф 2 - имф 2 + U 2 M ² ф 2 + ••• + ( - 1) l ^-1 U l ^1-1 M ^{1 1- 1} ф 2,

t иф = /(t — s)-“^(s)ds.

Решение третьей подсистемы определяется структурой решения уравнения Абеля первого рода [23]:

y a (t) = WN ⁰ ф з — W ² N 1 Ф з + ••• + (- 1) k W k ¹ N k ^1-1 Ф з ,                (9)

t

Wv = sin^d      Ws)  _ds.

к dt J (t — s) ^1- " 0

Таким образом решение x(t) может быть найдено как x(t) = Qy(t), где y(t) определяется по формулам (7), (8), (9).

Для иллюстрации приведем пример.

Пример 1.

(1 °

° 1 °°

°\       t        (° ° Л

° I x(t) + (t — s) ^- " I 1 ° ° I x(s) = f(t).

°)       0            \ ° 1 °)

Заменой x =

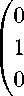
°1

° ° I y задача (10) сводится к системе

1°

t

Ny +

j (t — s) ^- " y(s)ds = f (t) 0

N ³ = °,

решение которой находится последовательным применением оператора (7).

3.    Численный метод

Для численного решения начальной задачи (1), (2) была предложена и реализована следующая разностная схема первого порядка:

i+1

A i+1 ^(x i+1 x i ) ^{+ hB} i+1 x i+1 ⁺ h ^ ^ W i+1,j K i+1,j x j = hf i+1 , i = °, ¹, 2, . . . , ^ ,       ⁽¹¹⁾

j=1

где N" — число узлов сетки, h = 1/N,

Ai+1 = A(ti+1 ), Bi+1 = B (ti+1 ), Ki+1,j = K (ti+1 , tj ), ti = ih, а веса Wi+1j находятся по формуле jh h1-"

^ i+1,j =        ⁽ t i+1 ^{— s)} " ^ds = ^      [ ^{(i —} j ^{+ 2)1} "  ^{— (i —} j ^{+ 1)1} " ] •

1 — a

(j - 1)h

Теорема 2. Пусть выполнены условия теоремы 1. Тогда

• 1)    начиная с некоторого h <  h * система (11) имеет решение V i € { 0, ^} ;

• 2)    справедлива оценка

max | x i — x(t i ) | <  Kh ^min( “’ ¹ ") , к = const > 0. i=0,N

Доказательство. Перепишем равенство (11) в виде

i

( A i+1 ^{+ hB} i+1 ⁺ h ^ i+1,i+1 K i+1,i+1 ) x i+1 — A i x i + ^h ^^^ i+1,j K i+1,j x j — ^hf i+1 -     ⁽¹²⁾

j=1

Согласно теореме 1, начиная с некоторого h < h*, матричный полином Ai+1 + hBi+1 + h2Wi+1,i+1 Ki+1,i+1 имеет простую структуру и не обращается в нуль. Далее, перепишем систему (11) в виде xi+1 — xi                  i+1

Ai+1    h    + Bi+1xi+1 + h ^ ^ ^i+1,j Ki+1,j xj — fi+1, j=1

введем замену переменной y + — S i+1 X i+1 и умножим полученную систему на R i+1 , где S i — S (t i ), R i — R(t i ), а R(t) и S (t) — матрицы из леммы 2. Таким образом, мы расщепили (12) на три подсистемы разностных уравнений, соответствующих системе ИДУ в нормальной форме, системе уравнений Вольтерра второго рода и системе уравнений Вольтерра первого рода, для каждой из которых сходимость доказана в классической теории (см., например, [6]).

Численный метод (11) был реализован в пакете прикладных программ MATLAB. Для анализа работы метода были использованы специально построенные модельные примеры.

Пример 2.

1 0 0\          /1

0 0 0 I X(t) + I 0

000     0

0 0\         t           Л 0 0\          А + 2 1 ^{5/ 3}\

1 0 I x(t) + (t — s) ^-1/3 I 0 t 0 I x(s)ds — I t + 10 1 ^8/3 I , 00)       0            \0 0 1)          \ 47 1 ^8/3 )

x(0) —

t € [0,1].

Легко проверить, что данная начальная задача удовлетворяет теореме 1. Здесь точное решение известно и имеет вид x(t) — (1,t, t ² ) ^т . Результаты расчета приведены в таблице:

Обозначения: Nset — число узлов сетки, err j — максимальная погрешность по каждой компоненте X j (t), j — 1, 2, 3.

Таблица

Результаты расчета для примера 2

Nset	егг 1	егг 2	егг з
90	0.010	0.011	0.023
270	0.005	0.008	0.016
810	0.003	0.004	0.009
2430	0.001	0.002	0.005

Если условия теоремы 1 не выполнены, то метод (11) неустойчив либо принципиально не применим. Чтобы проиллюстрировать сложность и неоднозначность изучаемых задач, рассмотрим следующий пример.

Пример 3. Для нижеприведенной системы не выполняется условие простой структуры:

t

0 I x(t) +

d 0\         t          /0

t 0 I x(t) + / (t — s) ^- “ I 0

00)     0         \0

0 t

0 0 I xUVls = f(t), t E [0,1],

^f(t) = ^(f 1 ^(t),^f 2 ^(t),^f 3 ^{(t)) T} , ^x(t) = ^(x 1 ^(t),^x 2 ^(t),^x 3 ^{(t)) T} .

При исследовании разрешимости системы (13) возникают следующие ситуации:

• 1)    d = 1: решение существует и единственно V f (t) E C 2 1] ;

• 2)    d = 1: система (13) разрешима тогда и только тогда, когда f i (t) — tf 3 (t) — f 2 (t) = 0. При этом одну из компонент (x i (t) или X 2 (t)) мы можем взять в виде произвольной вектор-функции из C 1 1] .

В то же время, при применении для решения системы (13) разностной схемы (11) необходимо учесть следующее:

• 1)    | d | < 1: метод (11) неустойчив, т.к. справедлива оценка x i+1 = О (d i) ;

• 2)    d = 0: решение системы (13) существует, но det (A i+1 + hB i+1 + h ² W i+1,i+1 K i+1,i+1) = 0 V h;

• 3)    d = 1: det (A i+1 + hB i+1 + h ² ^ i+1,i+1 K i+1,i+1) = 0 V h, но система (13) может не иметь решения.

Заключение

В статье на основе теории матричных пучков и фактов из теории численного решения интегральных уравнений проанализированы условия существования и единственности решения вырожденных систем ИДУ со слабой особенностью в ядре. К подобным математическим формулировкам приводит моделирование процессов, протекающих в электрических и гидравлических цепях, различных динамических системах, в частности, многотельных. Поэтому исследование и численное решение такого рода задач является актуальным, а результаты исследований — востребованными на практике. В работе было показано, что в случае постоянных матриц решение вырожденной системы ИДУ можно выписать в явном виде в терминах функции Миттаг-Леффлера. Предложен численный метод решения таких уравнений, который был реализован в пакете прикладных программ MATLAB и протестирован на модельных примерах. Показано, что в случае нарушения условий теоремы существования данный метод неприменим. Следующим направлением исследований является качественный анализ ИДУ со слабой особенностью в ядре, в которое искомая функция входит нелинейно, а также изучение работоспособности численного метода на реальных задачах из приложений.

Работа выполнена при поддержке РФФИ, проект № 20-51-54003.