Об одном методе обнаружения групп точек, объединенных принадлежностью к прямым линиям

Ososkov G., Rudenko M. About one method for detecting point groups, united by belonging to straight lines. System Analysis in Science and Education,   2021;(1):41–44(In Russ). Available from:

Введение

В различных системах, связанных с обработкой изображений, необходимо решать задачи поиска или идентификации некоторых объектов на этих изображениях. Одним из ранних инструментов для решения подобных задач стало преобразование Хафа, введенное в 1962 г. [1]. Оно позволяет выделять на изображениях прямые отрезки и другие аналитические объекты, даже если изображения зашумлены или объекты имеют разрывы. Модификации оригинального преобразования Хафа применяются для определения линий горизонта, распознавания контуров зданий, нахождения дорожной разметки, в задачах реконструкции событий в ФВЭ [2], в задачах ядерной физики [3]. Почти для каждой прикладной задачи такого рода вводится свой усовершенствованный метод, основанный на преобразовании Хафа [4].

Одной из таких модификаций является метод поворотных гистограмм (МПГ) [5]. Это быстрый алгоритм, который позволяет находить прямолинейные отрезки под любым углом на координатах измеренных точек. МПГ использовался, в частности, для нахождения характеристик будущей модели «тонкой структуры» в корреляционно-массовом распределении осколков деления ядра Калифорния ²⁵²Cf(sf).

В данной статье предлагается еще один алгоритм поиска прямых линий, для подобной задачи, где как это видно на рис. 1, человек может сразу выделить несколько групп точек, лежащих на прямых, но МПГ напрямую оказывается неприменим для распознавания сразу всех этих групп точек из-за небольших случайных вариаций по наклону и разбросу точек (т.е. ширин коридоров МПГ). Предложенный нами метод соседствующих точек (МСТ) оказался в состоянии покрыть узкими прямолинейными коридорами 91% групп измеренных точек, выбранных методом, как соседствующие.

Рис. 1. Пример с группами точек, объединяемых по близости к прямым линям

Метод соседствующих точек

МСТ основан на МПГ, вначале так же все точки проецируется под нужным углом и задается минимальное количество точек, чтобы идентифицировать структуру как линию и ширину отрезка. Далее, определяются проекции всех точек и слева-на-право подбираются ближайшие соседи. Если

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №1, 2021 год расстояние от первой точки до ближайшей меньше заданного порога, то точки считаются соседями и идет расчет расстояния до следующей, найденной точки. Если полученное расстояние больше порогового, то рассчитывается дистанция уже от первого соседа самой первой точки, и если полученное значение уже меньше порога, то первая точка перестает считаться соседом (см. рис. 2). Если же оба условия не проходят проверку, то идет проверка на количество соседей, при превышении ими минимального порога, можно судить о том, что нужная линия найдена. Алгоритм останавливается, когда обойдет все точки.

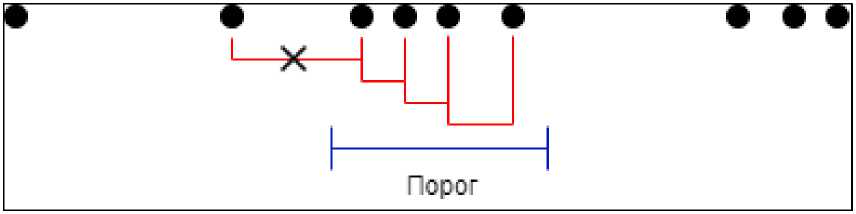
Рис. 2. Иллюстрация работы МСТ

Блок-схема алгоритма представлена на рисунке 3.

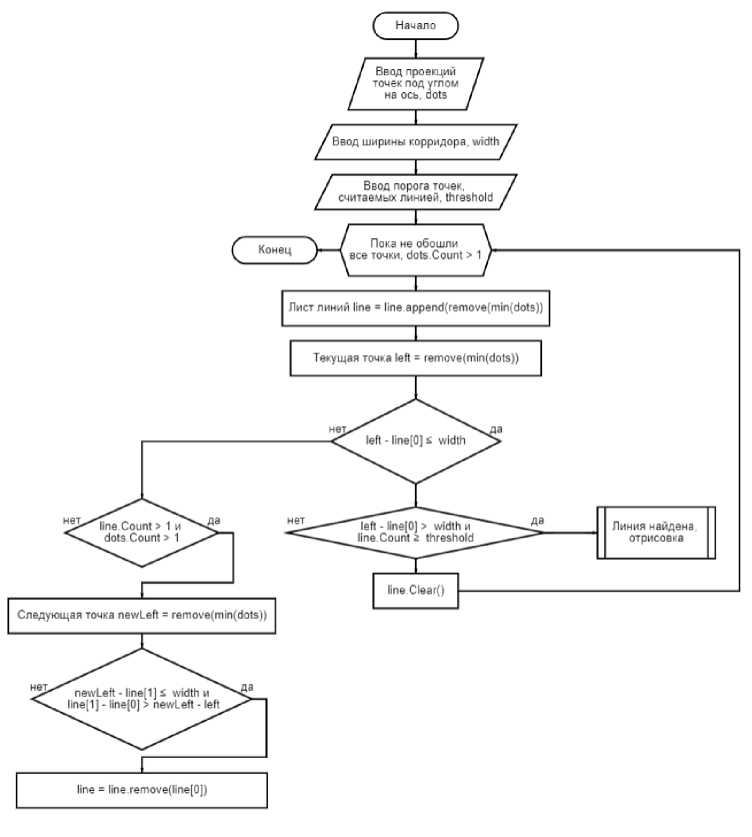
Рис. 3. Блок-схема МСТ

Плюсами данной реализации является то, что в случае с МПГ необходимо дополнительно решать проблему с перекрытием точек друг друга в разных столбцах гистограммы, иначе будет возможность потерять прямолинейный отрезок, либо не установить такой вовсе. МСТ лишен данного недостатка, довольно прост в реализации, а по скорости выполнения не уступает МПГ.

Первоначально метод соседствующих точек был реализован с помощью языка программирования Java SE 15.02, а далее повторен на Python 3.6, с использованием библиотек NumPy [6], из-за предоставления возможности работы с массивами и функцией тангенса, для просчета проекций, и Matplotlib [7], для получения графиков.

Заключение

Таким образом, предложенный нами метод соседствующих точек является еще одной из множеств альтернатив оригинальному преобразованию Хафа, но неоспоримом плюсом является его простота реализации, как при использовании интерпретируемых, так и компилируемых языков программирования.

Инструмент достаточно гибок, если не получается найти нужную прямую сразу, всегда можно подкрутить настройки так, чтобы найти ее, но точность при этом снизится, возможны появления линий там, где их при маленьком значении ширины коридора не было бы. Но это относится ко всему семейству алгоритмов работающих подобным способом.

В будущем в соответствии с запросом на обработку реальных измерений корреляционномассового распределения осколков деления тяжелых элементов планируется создание модели таких наборов точек, принадлежащих прямым, со случайными углами наклона в небольшом диапазоне около 45 градусов, случайным числом точек, распределенным по закону Пуассона, и случайно отстающих от своих прямых по нормальному закону. На этой модели планируется провести статистический анализ данного метода поиска таких групп точек.