Об одном методе построения единого потенциала
Автор: Стружанов Валерий Владимирович, Просвиряков Евгений Юрьевич, Бурмашева Наталья Владимировна
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 2 т.2, 2009 года.
Бесплатный доступ
Разработана методика построения в деформационных теориях неупругого деформирования единого потенциала, с помощью которого устанавливается связь между напряжениями и деформациями на всех стадиях деформирования, включая и стадию разупрочнения. Методика основана на подобии линий уровня потенциала при неупругом деформировании линиям уровня в области упругости. Рассмотрено растяжение с кручением, двухосное и трёхосное деформирование материальных элементов. Приведены примеры, иллюстрирующие методику.
Деформационная теория, единый потенциал, растяжение с кручением, двухосное растяжение, трёхосное растяжение, линия уровня
Короткий адрес: https://sciup.org/14320471
IDR: 14320471
Текст научной статьи Об одном методе построения единого потенциала
В деформационных теориях пластичности, как и в теории упругости, связь между напряжениями и деформациями задаётся конечными соотношениями. Следовательно, существует потенциальная функция, связанная с энергией деформаций. Например, в теории малых упругопластических деформаций [1] эта функция представляет собой сумму энергий изменения объёма и изменения формы и рассчитывается на основе гипотезы единой кривой. Однако во всех этих теориях учитывается только стадия упрочнения материала. В данной работе сделана попытка построить единый потенциал, способный описывать свойства материала в упругом состоянии, на стадиях упрочнения и разупрочнения. Введение такого потенциала необходимо для исследования устойчивости процессов деформирования и разрушения конструктивных элементов [2].
В работе рассматриваются среды, для которых в изотермическом активном процессе деформирования удельная энергия деформации Il(::) (Eij
—
компоненты
тензора деформаций, i , j = 1,2,3) отождествляется со свободной энергией на всех стадиях деформирования материала, включая и закритическую стадию (разупрочнение). Функция n ^ E ij .) равна удельной работе на непрерывной последовательности равновесных состояний, по которым среда переходит из натурального состояния в рассматриваемое равновесное.
Из данного предположения вытекает, что работа напряжений не зависит от вида пути деформирования, а определяется положением начальной и конечной точек в пространстве деформаций. Кроме того, функция П является потенциалом для
напряжений, то есть G j = dnjd& jj . Таким образом, в пространстве деформаций определено некоторое потенциальное силовое поле с потенциалом П .
В общем случае П — кусочно-дифференцируемая функция, и, следовательно, в пространстве деформаций имеется несколько силовых полей, и изображающая процесс деформирования точка, двигаясь в пространстве деформаций, переходит из одного поля в другое.
Если среда описывается непрерывно дифференцируемой функцией П , то в пространстве деформаций присутствует только одно силовое поле. В этом случае все поверхности уровня (для плоской задачи — линии уровня) потенциала П подобны поверхностям уровня для упругого материала и имеют замкнутую форму. Переход материала в состояние пластичности, а также достижение предела прочности происходит тогда, когда удельная потенциальная энергия принимает некоторые заданные значения, не зависящие от вида пути деформирования. Каждому такому состоянию отвечает конкретная поверхность уровня, что согласуется с энергетической теорией прочности Бельтрами–Хэйга [3]. Кроме того, существует предельная поверхность уровня, на которой потенциал имеет максимальное значение, равное работе разрушения (при одноосном растяжении работа разрушения равна площади, ограниченной полной диаграммой деформирования с падающей до нуля ветвью). Ясно, что величина работы разрушения не зависит от пути деформирования. Таким образом, условиями существования единого потенциала будет, как минимум, совпадение полных диаграмм растяжения и сжатия, а также равенство площадей, ограниченных полной диаграммой растяжения и полной диаграммой чистого сдвига.
Очевидно, что свойства материалов, по-разному сопротивляющихся растяжению и сжатию, не могут быть описаны единым потенциалом с поверхностями уровня, подобными поверхностям уровня, определённым для функции полной энергии деформации упругого материала. Кроме того, здесь не учитывается тот факт, что материалы могут выдерживать значительные гидростатические давления. Однако для путей деформирования, на которых реализуется обобщённое растяжение с положительным шаровым тензором, использование такого единого потенциала вполне оправдано.
-
2. Единый потенциал при кручении с растяжением (сжатием)
Рассмотрим полый цилиндрический образец специальных размеров, таких, что удлинение (укорочение) равно по величине деформации а , а деформация сдвига у равна по величине углу закручивания [2]. Деформирование осуществляется по жёсткой схеме посредством задания деформаций а и у .В данном случае линии уровня единого
, - Eа2 , GY2 / потенциала подобны линиям уровня потенциальной функции U = + (энергии деформации) при кручении с растяжением (сжатием) в области упругости. Они представляют собой эллипсы, центры которых совпадают с началом координат, а bE отношение главных полуосей составляет — = . — , причём наибольшая главная полуось aG расположена на оси Oу, а меньшая главная полуось — на оси Oа. Здесь Oау — прямоугольная (декартова) система координат, E — модуль Юнга, G — модуль сдвига. Теперь остаётся определить только значения, которые принимает единый потенциал U(а,у) на данных линиях уровня всех стадий деформирования. Для этого необходимо иметь полную диаграмму при растяжении или кручении. Отметим, что полную диаграмму хрупкого материала проще получить в эксперименте на растяжение [4] (отсутствует местное сужение — шейка), полную диаграмму пластичного материала — в эксперименте на кручение тонкостенных трубок [5]. Кроме того, полную диаграмму растяжения для пластичного материала возможно восстановить по результатам эксперимента на чистый изгиб балки прямоугольного поперечного сечения [6].
Возьмём на оси растяжения Oв произвольную точку s = к (деформация s отвечает неупругому состоянию материала). Очевидно, что точка s = к лежит на расположенном в плоскости Osy эллипсе (линии уровня потенциала U(s,у)), у которого малая полуось равна к, а большая — к
GE
Отсюда уравнение данной линии уровня имеет вид:
^+ g y 2 к 2 E к 2
= 1.
Тогда переменная к и координаты точек эллипса ( s,у ) связываются выражением:
к =
G s + — у2.
E
Теперь воспользуемся полной диаграммой растяжения a(s) и найдём значение единого потенциала U в точке к и, следовательно, на линии уровня (1). Это значение к равно Uк = j а (s)ds. Произведём замену переменной к в соответствии с равенством (2). 0
В результате, в силу произвольности к , получаем выражение для искомого единого потенциала U ( s , у ) .
Продемонстрируем использование методики на примере диаграммы растяжения, задаваемой формулой:
а <
—Г 1 + cos 2 L
J
,
0
0,1, 0,
s
>
0,1.
Тогда функция U к примет вид
U к
^к +——— sin (100 пк 2), 4 400п v 7
2,5 • 10-3 E, к > 0,1 .
Здесь значение 2,5 • 10 3 E — есть энергия, затраченная на разрушение. Наконец, с учетом выражения (2) получаем:
U (s, Y)
= C
E s 2 + G у 2
E
+----- sin 400 п
100 п
E
( E s 2 + G y 2 ) ,
5 • 10 - 3 E ,
( s , y ) ^Q , ( s , y)^ .
Это соотношение можно представить в виде
U ( s , y ) = <
Ue
— +
E
400 n
. ( 200 n sin
I E
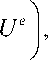
2,5 - 10 - 3 E ,
(s,7K^ , (s, y)^Q .
I 2 . 2 - E I
Область Q = < s, у : s, у> 0, Es + Gу < 100 Г найдена из уравнения эллипса (1) при значении s = к = 0,1.
На рисунке 1 показана поверхность, определяемая функцией (3), а на рис. 2, 3 — d U , . d U поверхности, задаваемые соответственно функциями t ( s , y l =--- и ^ ( e , у } = ,
dy ds которые определяют связь между напряжениями и деформациями при условии s, у > 0. Во всех случаях используются значения модулей E = 2 • 104 кГ/мм2 и G = 7,7 -103 кГ/мм2. Особенностью этих поверхностей является наличие восходящих и нисходящих участков, вызванных тем, что при построении потенциала используется полная диаграмма деформирования с падающей до нуля ветвью. На падающих участках данных поверхностей, как и на падающей ветви диаграммы растяжения, материал находится на стадии разупрочнения.
Отметим, что матрица тангенциальных (инкрементальных) жёсткостей имеет в данном случае три различных компоненты, а именно:
d2=d2U =dT = 52U = = 5т = 5о = 5 2U
, 22 , 12 21
ds ds dy dy ds dy dsdy
(в упругости c11 = E, c22 = G, c12 = c21 = 0). Это указывает на анизотропию, приобретённую материалом в ходе деформирования.
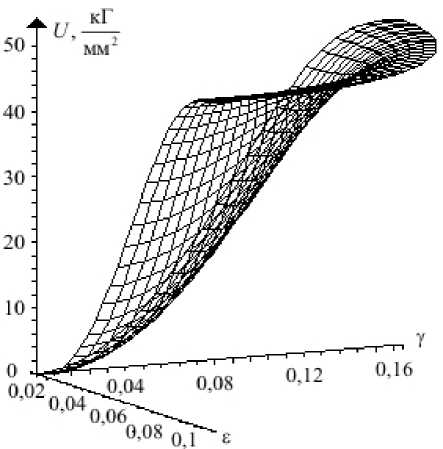
Рис.1. Геометрия потенциальной поверхности
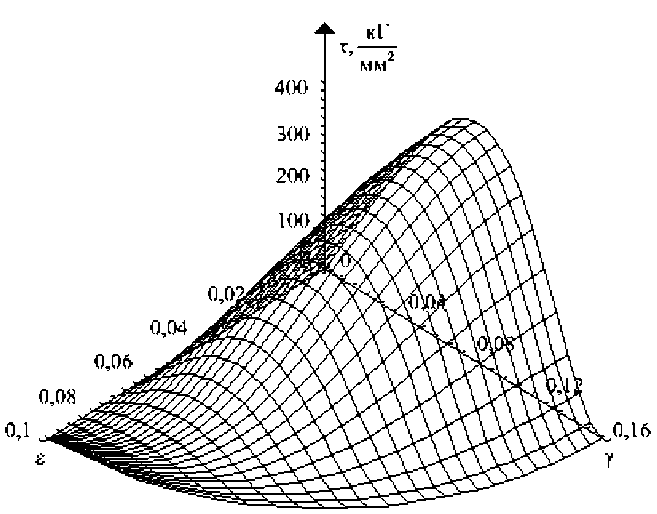
Рис.2. Поверхность, отвечающая двумерной функции т ( е , у )
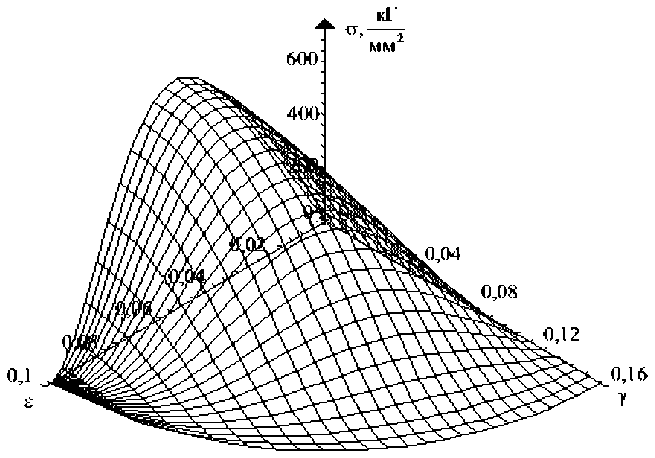
Рис.3. Поверхность, отвечающая двумерной функции ст ( е, у )
-
3. Единый потенциал при двухосном деформировании тонкой пластинки
Подвергаем деформированию тонкую квадратную пластину со сторонами равными единице, задавая деформации — продольную £ 1 и поперечную £ 2 , такие, что пластина сохраняет прямоугольную форму. Подобным образом реализуется двухосное напряжённо-деформированное состояние. Если материал остаётся упругим, то, используя определяющие соотношения для плоского напряжённого состояния, находим напряжения о 1 и ^ 2 , а затем и энергию деформации. Она равна
1 E
V = 2 (^£1 + °2£2 )= 2 (1 ^2 )(£1 + 2v£1£2 + £2 ).
Здесь v — коэффициент Пуассона.
При задании различных значений энергии V e выражение (4) определяет в прямоугольной системе координат O £ 1 г 2 кривые второго порядка, которые являются линиями уровня потенциальной функции V e . Чтобы найти вид этих кривых, повернём
П исходную систему координат против часовой стрелки на угол 4 . В новой системе координат Oe1e2 выражение (4) преобразуется к каноническому уравнению эллипса:
e L + e_ = 1
2 b 2
a
,
где a 1 2
SE
4 ( 1 -v ) 2 ( 1 + v ) 3,
b 2 =_____ SE ,
1 4 ( 1 -v ) 3 ( 1 + v ) 2
a 2 1 -v c rze
-^- =----, S = V . Линии уровня b 1 + v
функции V e , определяемые выражением (4), показаны на рисунке 4. В области неупругости линии уровня единого потенциала V подобны линиям уровня потенциала V e , то есть представляют собой эллипсы с тем же самым отношением главных осей. Неизвестно только распределение значений потенциала V по этим линиям уровня.
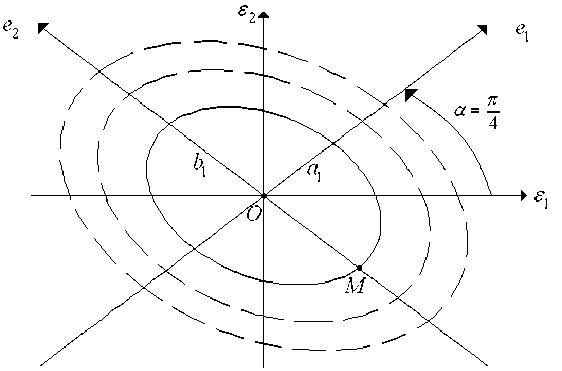
Рис. 4. Линии уровня функции V e
Для решения данной задачи возьмём на оси Oe2 произвольную точку M , отстоящую от начала координат на расстояние OM = р (Рис. 4). Очевидно, что точка M
I 1 - v
V 1+v
лежит на эллипсе, у которого большая полуось равна b = р , а малая — а 1 = р
Уравнение этого эллипса имеет вид
e£H+vl. e P2 (1 -v) р2
Отсюда
р =
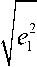
(1+v)1 - v
+ e 2 .
Далее воспользуемся тем, что путь деформирования, направленный по оси Oe 2 , реализуется при чистом сдвиге ( 8 1 = -8 2 ) . На основе полной диаграммы при чистом сдвиге т ( у ) находим энергию деформации:
р
V P = / т( у ) d У -
В силу сделанных ранее предположений величина энергии V равняется энергии V p , если точка M и точка, расположенная на произвольном пути деформирования, лежат на одной линии уровня. Тогда, делая в формуле (7) замену переменной р , в соответствии с формулой (6) получаем выражение для единого потенциала V ( e 1 , e 2 ) в новой системе координат. Для записи потенциала V в старой системе координат установим связь между новыми и старыми координатами [7]:
е1 =81 cos a + 82sin а = — (81 +82),
e 2 = -8 1 sin а + 8 2 cos а = ( -8 1 + 8 2 ) .
После замены переменных e 1 , e 2 на переменные 8 1 , 8 2 находим искомую потенциальную функцию V ( 8 1 , 8 2 ) (единый потенциал).
В качестве примера возьмём диаграмму т ~ у, заданную формулой
т = s
G У
1 + cos
( 100 n G
I E
0 <у< 0,16 ,
0 , у > 0,16.
Тогда
Vp=1
G P2 , E ■ —!— +--sin
4 400 n
100пG 2) ~ Pj,
6,4 - 10 — 3 G ,
0
0,16 ,
p
>
0,16 .
Производя замену (6), в новой системе координат имеем:
V
(
e
1
,
e
2
)
=
e
2
F2 +
e
22
1
- v
E +--
400
п
. 100
п
G (
2(
1
+ v
)
'П —-—
e -^--L
sin E k 1 - v ' 2
6,4
-
10
-
3
G
,
,
39,06
(
1,857
e
1
2
+
e
22
, 39,06
(
1,857
e
1
2
+
e
22'
Здесь область
39,06
(
1,857
e
1
2
+
e
2
)
<
1 получена из канонического уравнения эллипса (5)
при
р =
0,16
(
v =
0,3
)
.
Отметим, что при деформировании по пути
Oe
1
(
e
2
=
0,
8
1
= 8
2
>
0
)
можно найти полную диаграмму двухосного равномерного растяжения, а именно:
°
1
°
2
dV
(
e
1
)
G (1 + v)
de
1
= < 2 (1 - v)
e
1
1
+
cos
(100nG (1 + v) 2)I E (1 — v) e J , 0, 0 < e1 < 0,117, e1 > 0,117,
где
e
1
=
V2
8
1
=
72
8
2
(
8
1
=8
2
>
0
)
, что следует из формул (8).
Наконец, с учётом замены (8) получаем выражение для единого потенциала в старой системе координат
V
(8
1
,
8
2
)
=
G
(
8
2
+
2
v8
1
8
2
+ 8
2
)
E .
+
Sin
= <
4
(
1
-v
)
400
п
100пG (82 + 2v8182 + 82 )EO^) _
6,4
-
10
-
3
G
,
(8
1
,
8
2
)
^ ^
1
,
(
8
1
,
8
2
)
^Qp
которое может быть представлено в виде:
1
E .
, . - V
+-----Sin
V (81,82 ) = М 400п
100
л
V
E ,
6,4
-
10
-
3
G
,
(81, 82 )еЦ,
(8
1
,
8
2
)
^
Q
1
,
где область
Q
1
=
{
8
1
,
8
2
:
8
1
,
8
2
>
0, 55,8
(
8
2
+
0,6
8
1
8
2
+8
2
)
<
1
}
.
Геометрия поверхности, определяемой этой потенциальной функцией, имеет вид, аналогичный поверхности, изображённой на рисунке 1. Также и поверхности, задающие связь между напряжениями и деформациями < 5 V°1 = ^,( 58
5
V
д82 > аналогичны поверхностям на рисунках 2, 3. Матрица тангенциальных жёсткостей тоже имеет три ненулевых компоненты, отражающие анизотропию материала, возникающую в ходе неупругого деформирования.
4. Единый потенциал при трёхосном деформировании единичного куба
Деформирование единичного куба осуществляется по перпендикулярным к граням направлениям. Задаются нормальные деформации
8
1
,
8
2
,
8
3
таким образом, что куб может принимать только форму прямоугольного параллелепипеда. Потенциальная энергия упругих деформаций в этом случае равна
We = — ^(81 +82 +83 ) + 2р(8^ +82 + 83 ) . Здесь X, р — коэффициенты Ляме. Если задавать различные значения энергии We, то выражение (9) будет определять поверхности второго порядка (поверхности уровня) в прямоугольной системе координат O8.828..
В ортонормированном базисе
{
i
1
,
i
2
,
i
3
}
матрица квадратичной формы (9) имеет вид
2X + 2ц X A = X X + 2ц X X ) X X + 2ц v
Здесь
i
1,
i
2,
i
3 — единичные орты соответствующих координатных осей. Матрицу
A
можно рассматривать как матрицу симметричного преобразования пространства
R
3 (
R
3 — трехмерное евклидово пространство). Известно [7], что такая матрица может быть приведена к диагональному виду путём ортогонального преобразования базиса. Для определения такого преобразования воспользуемся собственными значениями матрицы
А
, которые равны 3
X +
2
ц
, 2
ц
, 2
ц
, и найдём сначала собственный вектор
а
1, отвечающий кратному собственному значению 2
ц
[7]. Очевидно, что существует только одно уравнение, позволяющее вычислить компоненты вектора
a
1 , а именно
X(81 +а2 + 83) = 0.
Отсюда вектор
а
1
=
{
1, 1, 1
}
. Соответствующий ему единичный вектор равен
Г
1 1 1
1 il
, ,
1 [7з V3 V3 Возьмём теперь любое решение уравнения (10), например, такое:
i
‘ = 1 —т= ,0, —7= г. Наконец,
2
I V2 V2 I
81 = -1, 82 = 0, 81 = 1. Нормируя его, получим вектор находим вектор i3 как векторное произведение i3 = ^х i2 =
1 2 1
1
V6, V6,V6
J
.
В результате получаем матрицу преобразования старого базиса в новый —
Г
, такую, что
А
= Г
А
Г-
1:
2
1
1
1
2
3
X +
2
ц
0 0
^
3
3
3
1
1
А'
=
0 2
ц
0 ,
Г =
0
2
2
v
0 0 2
ц J
2
1
1 V6
6
6
В новом базисе матрица
A
есть матрица квадратичной формы
We
=
(
3
X +
2
ц
)
e
^
+
2
ц
(
e
2
2
+
e
3
2
)
.
Здесь
Oe
1
e
2
e
3
— новая система координат с единичными ортами
i
‘
,
i
^
,
i
3
, полученная поворотом старой системы относительно начала координат. Косинусы углов между векторами
i
j
и
i
j
(
j
=
1,2,3
)
задаются элементами матрицы
Г
. Таким образом, при преобразовании старого базиса квадратичная форма (9) преобразуется в квадратичную форму (11).
Поверхность второго порядка (11) представляет собой эллипсоид, уравнение которого в новом базисе записывается в каноническом виде: eee
222
abc
2 Х + 2ц ,2 2 Х + 2ц b22 3Х + 2ц /, х _ где a 2 =-------, b2 = c 2 =------, —2- =-------(b2 > a 2). Главные оси эллипсоида 3Х + 2ц 2ц a 2 2ц направлены по осям новой системы координат. Используя компоненты матрицы Г, находим, что малая полуось (a2) направлена по оси Oe1, которая равно наклонена к осям Oе1, O£2, O£3, то есть перпендикулярна плоскости, равно наклонённой к осям старой системы координат (девиаторная плоскость). Две другие главные оси эллипсоида лежат в девиаторной плоскости, причём ось Oe2 есть пересечение девиаторной плоскости и координатной плоскости O£1£2 .
Итак, поверхности уровня единого потенциала
W
в области неупругости должны быть подобны поверхностям уровня функции
W e
, то есть представлять собой эллипсоиды с тем же отношением главных осей. Неизвестно только распределение значений потенциала
W
по этим поверхностям уровня.
Возьмём произвольную точку на оси Oe2 , отстоящую от начала координат на расстояние 5. Очевидно, что эта точка лежит на эллипсоиде, у которого большая полуось составляет b2 = 5 = c2, а малая полуось — a2 =5
2
ц
3
Х +
2
ц
. Уравнение этого эллипсоида имеет вид е2 (3Х + 2ц) + e2 + el = 1 2ц52 52 52. Отсюда . 3Х + 2ц 2 22 5 — --------e + e. + e,.(12) \ 2ц Далее, учитывая, что путь, направленный по оси Oe2 , реализуется при чистом сдвиге (£1 = -£2) , по полной диаграмме чистого сдвига найдем энергию деформации
W
5
=
J
t(
y
)
d
Y
.
Заменяя в выражении (13) переменную 5, в соответствии с формулой (12) получаем выражение для единого потенциала
W
(
е
1
, е
2
, e
3
)
в новой системе координат. Затем переходим к старой системе, используя связь между координатами, заданную равенством:
(
e
7
e
2
V
е
3
7
Г=!Л = Г =2 V=3 7 ^у— (=1 + =2 + =з)
^2
(
-
=
1
+=
—
)
( =1 - 2=2 + =3 )
В результате получаем искомый единый потенциал
W
(
=
1
,
=
2
,
=
3
)
.
В качестве примера возьмём диаграмму чистого сдвига, заданную выражением: т = Gу exp Г G у2
V
2
B
где B — величина энергии разрушения. Используя приведённую выше методику, находим:
W
B
Г
1
-
exp
V
G
5
2
)
2
B
J
W
(
е
1
,
е
2,
е
3
)
=
B
«
1
-
exp
G
-
V
2
B
3Х + 2н 2 2 2
------- ех
2
+
е
2
+
е
32 к
2
р
1 2 3
JJ
W (=!, =2, =3 ) = B ^1 -
=
B
1
-
exp
V w: ^
2
b
7
5 W Отметим, что определяющие соотношения оi =--- (i = 1,2,3), полученные с d=i использованием потенциала (14), геометрически представляются в четырёхмерном пространстве трёхмерными поверхностями с падающими участками, а матрица тангенциальных жёсткостей имеет шесть не равных нулю компонент:
d
2
W
д=
2
,
д
2
W
д=
i
д=
j ’
1
=
j
(
i
,
j
=
1,2,3
)
,
1 * j что указывает на приобретённую в ходе неупругого деформирования анизотропию материала. И, наконец, в пространстве инвариантов в области упругости
We
=
1
X+ 2^)d2 + цГ2 3 J
где
9 = =
,
+S
2
+ .
3
,
г
=
3
(.
,
+ E
+ E
i
-E
A
-E
|
E
i
-.
2
=
3
)
[8]. Тогда, подставляя выражение (15) в формулу (14), получаем функцию потенциальной энергии в пространстве инвариантов, то есть
W
(
3
,
Г
)
.
5. Заключение
Деформационные теории неупругого деформирования основаны на существовании потенциала напряжений. Выше приведена одна методика построения такого потенциала, описывающего свойства материала, как на стадии упрочнения, так и на стадии разупрочнения. Методика основана на том предположении, что линии уровня потенциала на всех стадиях деформирования подобны линиям уровня в области упругости. Работа выполнена по интеграционному проекту между Институтом машиноведения УрО РАН и Институтом гидродинамики СО РАН.
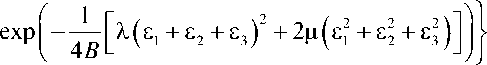
Список литературы Об одном методе построения единого потенциала
- Писаренко Г.С., Можаровский Н.С. Уравнения и краевые задачи теории пластичности ползучести. Справочное пособие. -Киев: Наук. думка, 1981. -486с.
- Стружанов В.В., Просвиряков Е.Ю. Растяжение с кручением. Сообщение 2: Устойчивость процесса деформирования образца в механической системе. Жёсткое и мягкое нагружение//Вестник СамГТУ. Сер.: Физ.-мат. науки. -2008. -№ 2 (17). -С. 77-86.
- Писаренко Г.С, Лебедев А.А. Сопротивление материалов деформированию и разрушению при сложном напряжённом состоянии. -Киев: Наук. думка, 1969. -212с.
- Миронов В.И. Свойства материала в реологически неустойчивом состоянии//Заводская лаборатория. Диагностика материалов. -2002. -Т. 68, № 10. -С. 47-52.
- Волков С.Д., Гуськов Ю.П., Кривосницкая В.И., Миронов В.И., Соковнин Ю.П., Соколов П.С. Экспериментальные функции сопротивления легированной стали при растяжении и кручении//Проблемы прочности. -1979. -№ 1. -С. 3-6.
- Стружанов В.В. Восстановление диаграммы деформирования материала по диаграмме чистого изгиба//Вестник СамГТУ. Естеств.-научн. серия. -2008. -№ 6 (65). -С. 322-328.
- Акивис М.А., Гольдберг В.В. Тензорное исчисление. -М.: Наука. -1969. -351 с.
- Лурье А.И. Теория упругости. -М.: Наука. -1970. -939 с.


