Об одном обобщении для решения начально-краевой задачи о колебаниях произвольного числа осцилляторов на стержне

Отметим важную особенность при рассмотрении начально-краевой задачи, если на стержне имеются два и более осцилляторов: колебательный процесс в этом случае меняется качественно, так как осцилляторы начинают взаимодействовать не только со стержнем, но и между собой.

Тогда можно ставить задачу о гашении колебаний части осцилляторов, оказывая влияние на перераспределение энергии между ними путем подбора начальных условий.

• 1.    Получение условия ортогональности

Рассмотрим механическую систему, представляющую собой однородный упругий стержень длины £, плотности р, модулем упругости Е, моментом инерции J поперечного сечения стержня относительно нейтральной оси сечения, перпендикулярной плоскости колебаний, с закрепленными на нем в точках с абсциссами а_к телами массами т_к, к = 1,2,..., п, посредством пружин с жесткостями с_к,к = 1,2, ...,п . Концы стержня жестко закреплены. Массы m_t могут перемещаться вертикально в направлении осей z_k . Колебания масс характеризуются функциями Zj Д) , перемещения точек стержня описываются функцией иД, t) .

Гибридная система дифференциальных уравнений, описывающая движение механической системы имеет вид [1]

• -ТГ + РкДк-^м<АДД = О

dt

Ди Ди Д дд*Ь— = ^екДк-иДД))5Д-ак), Д Дс где

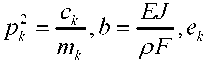
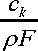
Краевые условия на концах стержня:

w(0, /) = м(/, /) = 0, ди , ди , ,      „

-(°,0 = -(/,0 = 0

дх дх

Представив z_k (f), и(х, t) в виде z_k (f) = А_к sin(crf + а_к ), и^х, f) = V(х) sin(trf + ^), подставив в (1), после преобразований получаем

-®24+а2(4-^Ж)) = 0 d4V(xA "                                 О) ®У(хуЬ      =^ек(Ак F(x))5(x а,) dx с краевыми условиями на концах стержня

И(0) = V^ = 0 <4) dx     dx

Запишем (3) для частот ®; и о:

-®^Aki^p1AAki-V1k^ = 0 ®z2^(x) + Z>2 =^ек(Ак1 №)№ A) dx      k=x "®"Ау+рк(Ау-У(ак')') = 0 7         t/V,(x) «                                       (6) 0yyy(x) + Z>    \ =^ek(Ay V^x^dCx ak)

Из (5) и (6) получаем выражения A_to, A_kj вида

Л, = -АЦ VMI                          <7> pk <8) Pk-®3

Перемножая их левые и правые части, получим

2            2 4A= , , , X MWM)                (9) Рк-®г Pk"®3

Проинтегрируем вторые уравнения в (5) и (6) по длине стержня. Тогда эти уравнения приобретут

вид	2J V.(xy (x)dx + b J= «             " Л    А                    (10)

L6

9ЧС[Хф 1ЧГКС1 Я ИИН9Ж(Ж£РС1 9Й1Я Я 1\9ГПИ (|) 1ЧИ91ЭИЭ ЭИНЭШЭД иьк№$ иояае(1я-онч1геькн эинэшэд "з

(Si)

o'!

уи         0

= W^ Z+*) ^^ ¹Л J

Гия 199ии июончгшнолояДо эияогэХ ‘pvocpdgo №DIPJ^

4dи            0

(И)

о = W^ ^+*) VlCO ‘A J

(б) кХсчгопэи ‘ним о = ( WvlC^OX

С,®- Ж^- X)

^Z + ^WvlOOXf

охи ‘минХиоп С ф z udu рГснэхо

( -о _ VY -о _      И            ⁰

о = ((Wa(Wa-—4j—— ^Z+^(x) riWXj)(^- i®)

PiHhXlfOn ‘ ^o— 4(0^ иядояэ P£ КЭОН1ЧЯ И ОЯ9ЕЯ 419Bh OiXflPdn КЭОН9С19Ц

W[aWa

1=^

= (Ъ)SlC’»)+ г yj )^Z = *)сл^‘а{(^- ^

г                 г                   11                                 1

(El) М9ИНЭНЯР(1Х О ИИЖОЕЭ И (з^) 9ИН9НЯР(1Х (р) РН мижонм^

(^^«''Ф'фа-е^'ле^'л^тФ- ’^=

(El)

= хр

^хр ^хр №йр"^Ул5

jq + xpCx)1^)^}-®-

fcl)

№[ЛСпуЛ^-СпУЛСпуЛ^-^^ = хр хр р                р

(ll)

(ll)^и (Ol) ихэрь giqppdn я (g) ‘(з) киярюгоц

(Мли’Ф'л-Й¥У^ =

О

о

WA,P(x)^PJ,           J/

энжdэшэ vh aodowKirirnhoo oironh ozomvoasnodu хкпнодэкоя о nhDQDE nosavdx-OHWvhVH umiamad kitq ппнэЫдодо wohqo gQ 'нодпжпу\[ ^у ‘эээтсну 'Q'j ‘aadadog 'j'g

=Е^^а, ^м(^х’0 =Еф.оуоо                  <¹⁶)

Z=1                                 Z=1

Подставляя в (1), получим

Фг (0 А + р²_к (ф, (0 А - ф_г (Ру (а_к )) = 0

ф. ОУ У)+Ьфг (0 4ж00 =                       оо ах

= ТА (^ (ОУ -Фг ОУ (х))^ (х - a J к=\

Разделив обе части двух уравнений в (3) на фУ , получим

^Ду+рМ ОУО = о Фг(О Ф1(?Ог00+ь , 4^(х) = ЕеДА 0(х)Жх afc) ФАО        dx        к=х (18) Обозначив 'Оя=-Юк Фг(О (19) получим -УУ+рКУ-оОУУ^ -®У (xyb^V^xyy^ек(Ab у (х))5(х-ак) dx          к=х (20) Таким образом парциальное движение является синусоидальным с частотой coi со смещением фj (Z) = Д sin соД + Д cos соД, (21) которое получается в результате решения дифференциального уравнения ф. (Z) + ft/A (Z) = 0, вытекающим из (19).

Запишем начальное условие

2 к (°) = Z Фг (°) А = Z ко ’ U (X, 0) =5 Фг WгОО = fl 00 Z=1Z=1

/уу

-А (0) = S Фй (0) А = Ztko — (°) =Z Ф 1г (°У А = /2 (х) ИЛИ dt Z=1                      St Z=1

£>Ж=^(22)

Z=1

У^Ф^УОхУА^(23)

Z=1

S%(°)A=^O(24)

Z=1

Z%(0A(x) = /2(x)(25)

Z=1

Умножим справа (22) на ^k О³ и просуммируем по к

Рк со       N р Д Д     N р 7 Д

Хфг(О)Х^!^ = Х^               (26)

И       к=1 Рк      к=А Рк

У множим (23) на Vj (х) и проинтегрируем по длине стержня

СО            I