Об одном обобщении интегро-дифференциального неравенства Виртингера

Математика. Механика. Информатика

Вып.2(6)

В работе получены условия справедливости интегро-дифференциального неравенства bb

J х2 (t) dt > \ (2px(t)x(t) + qx2 (t)) dt(1)

aa для функций с условием b

\ х (s) ds - 0,(2)

a являющегося обобщением известного неравенства Виртингера [ 1]

\х2(t)dt > \х2(t)dt. 00

При исследовании неравенства (1) с условием (2) применялись методы исследования вариационных задач, разработанные Пермским cеминаром по функционально-дифференциальным уравнениям [2], [3].

Обозначим через L₂ и через W ₂ пространство суммируемых с квадратом функций z : [ a ; b ] ^ R и, соответственно, пространство таких абсолютно непрерывных функций х : [ a , b ] ^ R , что х е L₂ . Суть метода состоит в редукции неравенства (1)–(2) в пространстве W к задаче минимизации квадратичного функционала b

\ ( z ( t ) - ( Kz )( t ) ) z ( t ) dt ^ min      (3)

a в пространстве L , где интегральный оператор K: L2 ^ L2 - ограниченный и самосопряженный. Как известно, задача (3) разрешима тогда и только тогда, когда все точки спектра оператора K не превосходят единицы.

Решение модельной задачи

’ ^{х (} t ) = z ⁽ t ), b

\ х ( t ) dt - 0,

. a

K = p ( w + W *) + qWW .

Найдем собственные значения интегрального оператора K . Отметим, что существование ненулевого решения уравнения Kz - A z эквивалентно существованию нетривиального решения системы

А х( t ) + qx ( t ) p (            ) - 0,	(4)
b - a bb \ х ( s ) ds - 0,	(2)
А х ( a ) - рх ( a ) - 0.	(5)

Достаточно рассмотреть случай А > 0 .

1 . Пусть q >  0 .

Общее решение уравнения (4) имеет вид

х ( t ) - C cos ^q ( t - a ) + C ₂ sin ^ q ( t - a ) + p ( х ( b ) - х ( a ) )

.

q ( b - a ) Обозначим a = ( b—a ) ^L . Система (4)-(2)(5) будет иметь нетривиальное решение при условии

p ( cos2 a - 1 )	p sin2 a	- q ( b - a )
sin 2 a	- ( cos2 a - 1 )	2 a	- 0
	2 aA
p	b - a	p

имеет вид х - Wz , где ядро интегрального оператора W равно

s - a

W ( t , s ) -<

b - a ’ b - s

b - a ’

если  a < s < t < b, если  a < t < s < b.

Подставив х = Wz в неравенство (1) сведем его к задаче (3), где

Это условие эквивалентно объединению

	L    ( b - a )2      7 A - q , , , , n е Z ,	(6)
A <  q	4 n n tg a - af 1 + А ] .          (7) L          I    p J Из   (6)   следует,   что   значение b - a )2                         q 2( b - a )2 —. Обозначим v - -^—и
4 n 2 запишем уравнение (7) в виде X 1 +  2 a    a		4 p 2 .                 (8)

Рассмотрим функции y (а) = -tg^   и а

Y у₂ ( а ) = 1 +—у при а >  0 .

а

2 а - sin2 a

Так     как      у 1 ( а ) =---₂---₂— >  0

2а2 cos2 а п              „ , „ при а > 0,   а ^- + пп, n = 0,1,2,..., то функция у; (а) монотонно возрастает в области определения. Функция у2 (а) при Y > 0, а > 0 является монотонно убывающей,

„ О (b - a) Fq   П_ где в = —~—v-. Отсюда получаем соотношение

в ( q A + p ² ) ch в - p ² sh в = 0,

равносильное уравнению

th в = в - — . в

Функция       у ₃ ( в ) = th в      ограничена:

так     как       у ‘ ( а ) = | 1 + - ^ l =- 2 ^ <  0.

V а ) а

Следовательно, на каждом интервале

- ^П + я п ; - ^Я + п (п + 1) | , где ^п = 0,¹,²,...,

Y

- 1 <  tg в <  1 . Функция y ₄ ( в ) = в -— моно-

In Y тонно возрастает, причем lim I в - —

-^ ,

существует единственное решение а

уравнения (8). Если а - наименьший корень

уравнения (8), то соответствующее значение

,    q ( b - a )²    _         ~

A =-----— будет наибольшим корнем

4а уравнения (7). Таким образом, условие Ао < 1

qq ( b - ^а )

эквивалентно условию а - ~—“---

. Тогда

lim в в ^«

—

у I

— 1 = » . Тогда существует наимень-

ший положительный корень во уравнения (9). - q ( b - a )²

Условие A =------—< 1 эквивалентно не-

4 в 02

равенству

th ( b - a )    q

( b - a ¹ J- q

^q p ²

tg 2

^q p ²

п2

( b - a )² .

K = p

3 . При q = 0 интегральный оператор ' ( W + W * ) , а общее решение уравнения

2 . Рассмотрим случай, когда q <  0 .

Общее решение уравнения (4) в этом случае будет представлено как x (t) = C sh ^-q (t - a) + Ci ch ^-q(t - a) + p (x (b) - x (a))

q (b - a)    , а система (4)–(2)–(5) будет иметь нетривиальное решение, если

p (ch2в -1) p sh2в - q (b - a) sh2в (ch2в -1) 2в = 0, 2вА p b - a p x (t) = C,( t - a) + C2 + i  xb'x^ (t - a )2.

2 A    ( b - a )

Система (4)–(2)–(5) будет иметь нетривиальное решение, если

2Ap 3AA 0  (pA- 2A) 6A     A2 = 0 , (10) A -p     0 где A = b - a . Условие (10) эквивалентно a|p| равенству A =     . Следовательно, если

( b - a )| p l

----f —¹< 1, то все собственные значения

23    , оператора K не будут превосходить единицы.

Таким образом, доказано следующее утверждение.

Теорема 1. Для всех функций x g W₂ неравенство (1) с условием (2) верно тогда и только тогда, когда

—

p² <  1 —

q th (b^a)

p ² <  ^^т ( b — a ) J q ^S

при 0 <  q <

q

.⁽ b ^— a ) Г

п2 (b—О)2;

2       ¹²

p < ——г? при q = 0.

( b — a )

Отметим, что искомое множество па- раметров имеет вид

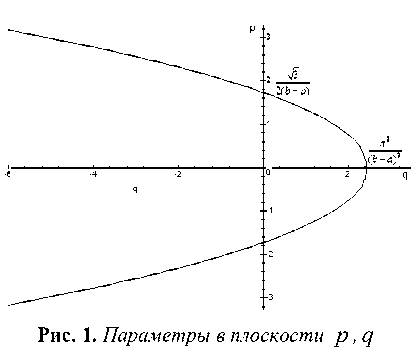
ющим образом: найти условия справедливости неравенства bb j x2 (t) dt >j (2 p.x( t) x (t) + qx2 (t)) dt     (1)

при q <  0;

a с условиями	a b j x ( t ) dt = 0 , a	(2)
	x ( a ) = x ( b ).	(11)

b

Но тогда j 2 p.x ( t ) x ( t ) dt = 0, и задача (1)-(2)- a

• (11)    эквивалентна классическому неравенству Виртингера, для которого справедлив известный результат.

Теорема 2. Для всех функций x g W₂ неравенство (1) с условиями (2) и (11) верно ²

тогда и только тогда, когда _q <   ^{4 п}   .

q~ ( b — a )²