Об одном подходе к моделированию динамических систем

Для того чтобы детально исследовать динамические процессы вычислений на компьютере, необходимо удобное представление алгоритмов, областей их определения и значений с точки зрения построения новых программ или функций на основе заданных базисных функций по заданным правилам. Одной из основных задач является построение базисных функций. Тогда любая программа будет представлена в виде суперпозиции базисных функций. Для того чтобы решить указанную проблему, мы используем следующие формально точные понятия (математические примитивы): конечное множество структурно согласованных контекстно-свободных грамматик; операция отождествления; универсальная функция eval (аналог интерпретатора ЛИСП) в терминах КС-грамматик; рекурсия; многоуровневость понятий, которая является естественной для формальных грамматик; формальные модели различных типов памяти: память с варьируемой структурой, с постоянной структурой и управляющая память. Данный указанный перечень математически точных понятий (примитивов) позволяет построить математическую модель языка программирования (ММЯП), которая, в свою очередь, позволяет моделировать на компьютере различные динамические системы.

1.    Постановка задачи

В данной статье требуется построить модель, которая для любой заданной синтаксически правильной программы х в языке программирования общего назначения (Алгол 68, С++, Паскаль и т. д.) указывает способ представления отображения из области определения (входные данные) в область значений (выходные данные). Данное отображение индуцируется программой х в виде алгебраического терма F е T ( О ), где T ( О ) — множество всех термов в языке L , О — сигнатура базисных функций языка L . Для этого необходимо представить семантику языка программирования L в виде алгебраической системы ( M , О ). При запуске программы х порождаются вычислительные процессы. Относительно этих вычислительных процессов в выбранных точках программы (алгебраического терма T ( О )) можно сформулировать интересуемые нас утверждения, представленные в различных видах: в виде позитивно образованных формул [1], в виде формул языка логики первой и второй ступеней алгебраической системы и т. д. Чтобы представить произвольную программу х языка L в виде алгебраического терма F е T ( О ), необходимо построить систему базисных функций

О = {Ф 0(1),..., ФN Ф (Г ,..., ФN(m)}.

Синтаксический анализ заданной программы х дает в качестве результата суперпозицию базисных функций F е T ( Q ). В статье показано, как можно построить алгебраическую систему для заданного языка L. При конкретной реализации языка программирования L универсальность рассматриваемой модели T ( Q ) ограничивается множеством допустимых состояний памяти. При первом приближении это может быть обусловлено количеством выделяемых разрядов для представления чисел , количеством букв в строке (строковые данные) и т. д. Если более детально разобрать вопрос о множестве допустимых состояний памяти (ОДСП), то необходимо рассматривать представление структуры различных видов значений в памяти компьютера. Под различными видами данных подразумеваются числа (целые, вещественные, комплексные); логические значения; представления процедур и т. д. Для того чтобы формально описать структуру различных достаточно нетривиальных видов данных в указанном подходе используются многоуровневые грамматики видов и значений. Формально можно описать ОДСП пятеркой (V , B , G 1 , G ₂, G ₁), где V — множество переменных программы, B = { b : V ^ M } — множество всех частичных отображений множества переменных V в M , где M — множество значений, которые индуцируются грамматиками G 1 , G ₂, G - 1 . Здесь G 1 — грамматика видов данных, G ₂ — грамматика значений, G 1 — грамматика структуры представления данных во внутренней памяти, которая формально описывает структуру представления всех видов значений. Для представления сложных межвидовых логических отношений, помимо вышеуказанной пятерки, можно ввести функции приведения одних видов в другие. Ниже в приложении приведены некоторые примеры таких функций: g 1 ⁽¹⁾, g *²⁾, g 21) , g 22) . Эти функции вводят частичный порядок на множествах M - 1 , M ₂, которые порождаются грамматиками G 1 ,G ₂ соответственно.

2.    Способы построения функций в терминах формальных грамматик

Для решения поставленной задачи использование КС-грамматик тесно связано с внедрением именных множеств: нетерминальные и терминальные символы образуют имена множеств, элементы которых являются словами в некоторых алфавитах. В связи с этим рассмотрим понятие имя более подробно. Понятие имя в программировании и в компьютерном моделировании играет фундаментальную роль. Если смотреть на задачу с точки зрения прагматики, то постановщик задачи имеет дело с предметно-ориентированной логикой: имена понятий, имена объектов, имена отношений между ними и т. д. С другой стороны, компьютер имеет абстрактные пронумерованные ячейки памяти, у которых номера ячеек явля- ются их адресами, а также абстрактные машинные операции либо абстрактные операции языка программирования общего назначения, оторванные от предметной логики. Для построения модели предметной области, прежде всего, необходимо найти удачное представление элементов именного множества для максимального упрощения предметноориентированных операций, функций, предикатов и формул предметной области в памяти разрабатываемого приложения вместе со всеми их свойствами и отношениями (единицы измерений значений переменных). При разработке приложения разработчик всегда вынужден выполнить переход-операцию от более общих абстрактных понятий-имен к более конкретным предметно-ориентированным понятиям-именам. В связи с этим становится актуальной работа с именами, обозначающими понятия и их интерпретации: 1) операция разыменования; 2) операция именования. Для построения адекватной цифровой модели предметной области с каждым именем (объектом, понятием) взаимно-однозначно связывается неизменный адрес памяти. Таким образом, в данной работе понятие имя и его адрес отождествляются. На основании вышесказанного в работе выбран язык программирования с расширенной концепцией косвенного именования, для которого строится универсальная алгебра (M, О), являющаяся моделью семантики заданного языка.

Рассмотрим конкретно операции разыменования и именования на примере реализации семантики этих операций средствами функциональных грамматик. Для этого рассмотрим семантику языка программирования ASPLE с многократной адресацией, где наиболее наглядно демонстрируется семантика именованных множеств. В [4] проводится сравнение четырех подходов к формальному описанию языков программирования на примере простого подмножества языка Алгол-68. В данной работе выбрана двухуровневая универсальная схема вида:

Y(M-1, L(G0), M,, M2,ф/(1)},{Ф/(2)}, {gjn },{g;2)}), где M-1 — множество всех переменных типа конт, G0 — КС-грамматика, задающая синтаксис языка ASPLE, L(G0) — множество текстов программ, M 1— множество видов, M2 — множество значений, {Ф?0)} — конечное множество функций (алгоритмов) на уровне видов M1 , {Ф?(2)} — конечное множество функций (алгоритмов) на уровне значений M2, {gjn } — конечная система преобразований видов, порождающая частичный порядок на множестве M 1, {gj2)} — конечная система преобразований значений, порождающая частичный порядок на множестве M2 . Множества M-1,M 1, M2 порождаются КС-грамматиками G-1, G1, G2 соот- ветственно. Построение алгоритмов {Фi(1)},{Ф1(2)},{g*n},{g*2)} в терминах этих грамматик является основной задачей конструктивного определения математической модели языка программирования. Внешняя грамматика G0 представляет собой четверку:

G = < V V Р А > 0 T0, N0’0’0’ где VT0 — множество терминальных символов, VN0 — множество нетерминальных символов, P0 — множество правил вида

A. ^ x.A_.x,A_, ... x,A_,x. .( Фi ⁽¹⁾),                       (1)

i 1 1 12 1 2        k ik k + 1

A ₀ — начальный символ грамматики.

*

Обозначим множество терминальных цепочек через V _{T 0} , а множество

*                          ,^.(1)

сентенциональных форм через ( V _{T 0} и V N ₀ ) . Алгоритм Ф1 для соответствующего нетерминала A i будет иметь следующий вид:

Фi ⁽¹⁾ = ( < mun >, у ..,..., < mun >, у., ) <  mun > :

О Az S ^{( e 1)}z    z V ^e m ’z

... , Q ) Z S Z ... Z S Z

’ ik ' 1 1 1      2 m tm m + 1

где z j — терминальная цепочка одной из грамматик. Основную роль в указанных алгоритмах Ф1 ⁽¹⁾ играет операция отождествления, которой можно дать следующее определение. Пусть задана КС-грамматика

G m = ( V n , V t , P , S ) , которая порождает множество M , где

M = { x | x - слово, порожденное грамматикой G _M из некоторой сентенциальной формы G _M }.

Каждая функция Ф1 определена на некотором подмножестве декартовой степени множества M со значениями во множестве M . Пусть Ф, v — слова в алфавите VN и VT (сентенциальные формы грамматики G), где нетерминальные символы помечены индексами, которые являются формальными параметрами операции отождествления. Тогда операция отождествления синтаксически представляется в виде (ф) v и содержательно определяется как отображение совокупности входных формаль -ных параметров, принадлежащих к ф, на совокупность выходных (т. е. результирующих) формальных параметров, входящих в v . Семантически операция отождествления (ф) v трактуется так: если x — фактический аргумент этой операции, то строится вывод ф ^* x этого слова в грам- матике GM . Тогда нетерминальные символы слова ф получают в качест- ве значений некоторые подслова слова х (одинаковые нетерминалы, помеченные одинаковыми символами, должны принимать одни и те же значения), слово v определяет результат этой операции.

В общем случае операция отождествления неоднозначна. С целью достижения однозначности введем операцию левого отождествления: самый левый нетерминал в слове ф будет получать в качестве значения минимальное по длине подслово слова х [2; 3]. Сказанное продемонстрируем на примере.

Пример 1. Пусть задана простейшая грамматика G M :

M : : = AM | BM | е ; A : : = aA | a ; B : : = bB | b .

Рассмотрим функцию f = ( ABA ) BAB ; ф = ABA , v = BAB . Пусть х = a n b^maⁿ . Тогда вывод ф ^ х определит значения для A и B : A = a ” , B = b m . Результат равен v = BAB = b™aⁿb™ .

Необходимо подчеркнуть важность операции отождествления ( ф ) v в процессах обобщения и конкретизации функций (функциональных понятий) совместно со следующими нижеперечисленными операциями и концептуальными элементами: КС-грамматика для описания синтаксиса и структуры данных, описание суперпозиций функций и операции eval и quote (аналоги операций из Лиспа), описание множеств M для описания управления данными и памятью, память для описания структуры управления последовательностью действий, рекурсия, альтернативная операция A | B , управляющая память, функции приведения, многоуровневость языка .

Пример 2. Пусть задан фрагмент программы:

начало цел v , l ; имя имя цел a ; . „

Рассмотрим на данном фрагменте, как работает система базисных функций

Q- {Ф 0⁽¹⁾ ,..., ФN ⁰⁾, Ф 0⁽²⁾ ,..., ФN ⁽ m ) } .

Результатом будет следующая лемма.

Лемма 1 . В памяти формируется в соответствии с ОДСП следующая структура данных:

v * 1# v 1 *неопр# l * 1# l 1 * неопр# a * 1# a l * 2# a 2 * неопр# mF .

Доказательство. Предположим, что начальное состояние памяти до объявления переменных равно emF , где F — файл ввода. При входных данных цел v для указанной базисной функции Ф 6= (текст х , у ) знач: (ВИД, X ) r (имя ВИД, X *1# X 1, ВИД) имеем сопоставление: ( цел, v ) r ( имя цел, v * 1# v 1, цел ). Для Ф 5 = (знач х , текст у ) знач: (ВИД & M , X ) r (ВИД, MX *1# X 1*, ВИД) имеем сопоставление: (имя цел & M , l )

r (имя цел, Ml * 1# 1 1 *, имя цел) . Таким образом, сопоставляя каждому нетерминальному символу (формальному параметру) его фактические параметры (значения), можно вычислить остальные функции, фигурирующие в узлах синтаксического дерева разбора: Ф 2, Ф 6 и Ф 3. Результат последовательного вычисления указанных функций даст следующее состояние памяти:

v * 1# v 1 *неопр# 1 * 1# 1 1 * неопр# a * 1# a l * 2# a 2 * неопр# roF , что и требовалось доказать.

Пусть грамматики G-1, G1, G2, порождающие множества M-1, Mi, M2 соответственно, имеют вид G-1 = (VT-1, VN-1, P-1, A-1) , G1 = (VT 1, VN 1, P1, A1) , G2 = (VT2, VN2, P2, A2) . Общим и наиболее естественным требованием к построению грамматик G 1, G1, G2 является требование об их структурной согласованности. Грамматика Gi (L(Gi) = Mi) называется структурно согласованной по терминальным символам {а 11,...,aik} = V^j с VT с грамматикой Gj (L(Gi) = Mi) тогда и только тогда, когда каждому at G V сопоставлено однозначно некоторое подмножество Mj подслов слов множества   Mj   так, что каждому слову x = at1at2... am е (VT'.j) будет соответствовать подмножество M^1,..., M^ множества M . j

Структурная согласованность грамматик G - 1 , G 1 , G ₂ требуется для выразительного построения логики базисных функций языка. Под структурной согласованностью будем понимать логическую и смысловую связь именованных нетерминалов и терминальных строк, которые диктуют необходимость построения семантических отображений      {Oi ⁰⁾},{ Ф/ ⁽²⁾},{ g *^П},{ g j ²⁾}.     Другими словами,

V N1 ⁿ V N1 ⁿ V N ₂ *® , V _T1 ⁿ V ⁿ V T2 *® • Сказанное продемонстрируем на следующих грамматиках G 1 и G ₂, где G 1 — грамматика видов переменных, а G ₂ — грамматика значений переменных языка ASPLE. Содержательно нетерминал-понятие АБСТР из грамматики G 1 обозначает уровень абстракции или двойственное ему понятие — уровень конкретизации.

Грамматика G 1 = ( V T 1 , V N 1 , P 1 , ПРАВИД) — структура видов. ПРАВИД : : = ВИД | ничто ; ВИД : := АВИД | АБСТР ВИД;

АВИД : := лог | цел ; АБСТР : := £ | АБСТР имя ; Упорядоченность на M 1 : g *¹) = ( имя ВИД) ВИД.

Пара структурно согласованных нетерминалов АБСТР из грамматики G₁ и ЦЕПЬ из грамматики G ₂^т моделирует концепцию косвенного именования. ЦЕПЬ является конкретизацией АБСТР. G ₂⁽¹⁾:

ПРАЗНАЧ : := ЗНАЧ | неопр ; ЗНАЧ : := АЗНАЧ | ЦЕПЬ АЗНАЧ ;

АЗНАЧ : := ЛОГ | ЦЕЛ ; ЦЕПЬ : : = £ | ЦЕПЬ XH # XH *;

ЦЕЛ : := ЦЦЦ | неопр ; ЛОГ : := истина | ложь | неопр ; H : := £ | Ц | ЦЦ | ЦЕЛ ; Ц : := 0 | 1 | 2 ... | 9 .

Упорядоченность на M - :

g^<2) = ( конт t , знач x ) знач : ( M # XH * PM⁰⁾mF , XH ) P .

Из представленных грамматик видно, что существует квазиизоморфизм, т. е. некоторое подобие изоморфизма, а именно:

ПРАВИД ^ ПРАЗНАЧ ; ВИД ^ ЗНАЧ; АВИД ^ АЗНАЧ;

АБСТР ^ ЦЕПЬ; имя ^ H # XH * ;

лог ^ ЛОГ : : = истина | ложь | неопр ; цел ^ ЦЕЛ :: = ЦЦЦ .

Из вышесказанного видно, что грамматика G ₂⁽¹⁾ является продолжением грамматики G ₁ : терминальные символы грамматики G ₁ находят дальнейшую конкретизацию. Грамматику G ₂^т назовем продолжением грамматики G₁ по терминалам имя, лог, цел.

Для улучшения читабельности семантической функции присваивания Ф7(1) и Ф7(2) (верхние индексы (1) и (2) указывают, что данные функции рассматриваются на уровне видов и значений соответственно, однако, возможно, индексы будут опускаться, если это не будет приводить к путанице) необходимо преобразовать в сторону упрощения грамматику G2(1), используя идею косвенного именования: громоздкий нетерминал ЦЕПЬ заменим на XH для упрощения алгоритмической обработки и понимания сложноструктурированной информации, которая находится в сжатом виде в списке. Для этого достаточно иметь имя XH (head-list) вышеупомянутого списка. Семантические смыслы нетерминалов ЦЕПЬ и H неразрывно связаны: ЦЕПЬ является списком; нетерминалы X и H вместе являются начальным адресом отрезка списка ЦЕПЬ в момент исполнения функций Ф5, Ф6, Ф7 ; XH есть ячейка, содержащая ссылочный адрес на следующий элемент списка. Конкретное значение есть список, однако для однозначного задания значения достаточно указать на- чальный адрес списка XH. В связи с этим выполним преобразование, которое упрощает грамматики G2(1) в грамматику G2:

ПРАЗНАЧ : := ЗНАЧ ; ЗНАЧ : := ЦЕЛ | ЛОГ | XH I неопр | г ;

ЦЕЛ : := ЦЦЦ ; ЛОГ : := истина | ложь ;

H : := ЦЕЛ ; Ц : := 0 | 1 | 2 | 3 ... | 9 ; X : := <бкв> | X <бкв> .

Принципиальным является то, что семантическая нагрузка на XH увеличивается, так как в данном случае XH является значением и одновременно косвенным именем всей сложной цепи, представляющей собой сложноструктурированное значение. При этом описание функций Ф 5⁽²⁾, Ф 6⁽²⁾, Ф 7⁽²⁾ на уровне значений значительно упростится. Данный прием косвенного именования через XH дает нам гибкий инструмент для управления областями видимости объектов при многоуровневом моделировании.

При статическом объявлении переменных в блоке программы для каждой переменной отводятся фиксированные места в памяти, например, если объявлена переменная имя цел v , то в памяти образуется структурированный список следующего вида:

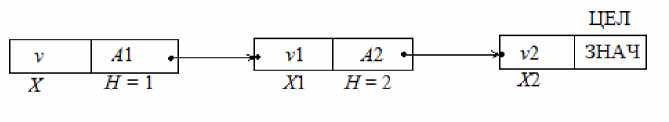
Рис. 1. Структура переменной в памяти

Адрес A1 отождествлен с переменной X и указывает или именует место в памяти следующего элемента списка. В данном случае A 1 (при H = 1 ) является адресом второго элемента списка ( v 1, A 2). Адрес A 2 (при H = 2) является адресом третьего элемента списка. Данный алгоритм обрабатывает объявления переменных и формирует ОДСП. ОДСП имеет ограничения, продиктованные структурой представления переменных внутри памяти. В качестве примера ограничения ОДСП можно сформулировать следующую лемму. Пусть т ₀ принадлежит набору элементарных типов { цел, вещ, компл, литера, проц, лог }.

Лемма 2. Если переменная X в программе объявлена в виде « имя T 0 X », то в соответствии с алгоритмической моделью О = {Ф0⁽ (1 ,..., ФN (1) , Ф0⁽ 2 ,..., Ф\ ' } формируется список вида X *1# X 1*2#...# XH * т ₀, где H = n + 1.

Доказательство проводится методом математической индукции в соот -ветствии с алгоритмами ( Ф 2⁽²⁾, Ф 5⁽²⁾, Ф 6⁽²⁾ , r ) , которые приведены в разделе 3.

Рассмотрим операции приведения данных от одного вида к другому. Операция привидения формально описывает логистику типов данных для упрощения построения алгоритмов над типами данных. Для этого рассмотрим пример в виде фрагмента программы на ASPLE:

начало {к₀} имя ² цел l ; цел v ; {k i } l := 2 ; v := 15 ; {к₂} l := v {к₃} конец .

В фигурных скобках мы расставили точки для комментариев.

{к₀}: в данной точке состояние памяти будет следующим smF , где £ — пустая память.

{к 1 }: состояние памяти согласно леммам 1, 2 будет:

l *1# l 1 * 2# l 2 * 3# l 3 * неопр# v * 1# v 1 * неопр#

{к 2 }:            l *1# l 1*2# l 2*3# l 3*2# v *1# v 1*15#

{к3}: в данной точке типы заданных аргументов для операции присваивания отличаются.

На начальном этапе рассматривается данный вопрос на уровне видов. В данной операции участвуют на уровне видов следующие функции: операция присваивания Ф7(1)= (знач x, у) знач: ( имя ВИД, ВИД) имя ВИД и операция преобразования видов g*1) = (имя ВИД) ВИД. На вход Ф7( первый фактический аргумент l имеет тип имя2 цел, а второй фактический аргумент v имеет тип цел. Однако формальные аргументы функции Ф7(1) имеют типы: первый аргумент имя ВИД, а второй аргумент ВИД. Непосредственное сопоставление фактических аргументов к формальным не удается: у первого аргумента одно лишнее имя. В таком случае система автоматически однократно вызывает вспомогательную функцию g1(1)= (имя ВИД) ВИД и преобразует первый аргумент к виду имя цел. И при этом когда на уровне значений запускается функция Ф7(Т}, то она автоматически аналогично однократно вызовет для первого аргумента вспомогательную функцию на уровне значений g= (конт t, знач x) знач : (M #XH * PM(1)mF, XH) P.

Если бы переменная l имела вид « имя n цел l », то в таком случае вспомогательная функция на уровне видов g *¹) = (имя ВИД) ВИД встраивалась бы в текущую суперпозицию на вход операции присваивания автоматически ( n - 1) раз, и соответственно на уровне значений функция g 22) = (конт t , знач x ) знач : ( M # XH * PM⁽¹⁾mF , XH ) P вызывалась бы автоматически ( n - 1) раз. Другими словами, вычисление на уровне видов дополняет суперпозицию базисных функций необходимым количеством вспомогательных функций для преобразования видов, чтобы на уровне значений мы получили изоморфную суперпозицию базисных функций, являющуюся моделью программы.

Если обозначить за х текст программы, F 1 — суперпозицию базисных функций на уровне видов, F 2 — суперпозицию базисных функций на уровне значений, { g *¹’} и { g *²⁾}— функции преобразования видов, то схему работы построенной модели можно представить следующим образом

, алгоритм           исполнение F/1'    .       . изоморфное _

• ¹  ----^----* Fi^ ---------* Fj*- {gi^} ----"--> F₂^ + fgt®}

3.    Алгебраическая модель языка программирования

синтаксического                                    отображение разбора

Рис. 2. Схема работы построенной модели

Готовая для исполнения программа порождает процесс моделирования динамической системы.

Используя вышеописанное, построим полное формальное определение синтаксиса и семантики языка ASPLE.

Грамматика G _ 1 = ( V T _ 1 , V N _ 1 , P _ 1 , E ) — модель памяти типа конт .

• 1.    E : : = MmF ; M — внутренняя память, F — входной и выходной файлы;

• 2.    M : : = ВИД X # M | X * ЗНАЧ # M | £ ;

• 3.    F :: = B § B ;

• 4.    B : : = B * ЗНАЧ | £ ;

Начальное состояние памяти: E = £юВ § £ , где B — файл ввода.

• V t _ 1 = { ю , §, *,#, £ , X ,ВИД,ЗНАЧ} , V n _ 1 = { E , M , F , B }.

Грамматика G 0 = ( V T 0 , V N 0 , P 0 , <  программа >) — синтаксис.

• < программа > : : = начало < описания > ; < операторы > конец Ф1

< описания > : := < описание > ; Ф 2 | < описания >< описание > ; Ф 3

< операторы > : : = < оператор > ; Ф 0 | < операторы >< оператор > ; Ф 4

< описание > : : = < описание > , X Ф 5 | ВИД X Ф 6

< оператор > : : = < оператор присваивания > Ф 0 | < условный > Ф 0 |

< цикл > Ф 0 | < условный > Ф 0 | < ввод-вывод > Ф 0

< оператор присваивания > : := < идент > := < выражение > Ф 7

< условный > : : если < выражение > то < операторы > все Ф 8

если < выражение > то < операторы > иначе < операторы > все Ф 9

< цикл > : : = пока < выражение > цикл < операторы > конец Ф 10

< ввод-вывод > : : = ввод X Ф11 | вывод < выражение > Ф 12

< выражение > : : = < множитель > Ф 0 |

< выражение > + < множитель > Ф 13

< множитель > : : = < первичное > Ф 0 | < множитель > *< первичное > Ф 14

<первичное> : : = < идент> Ф 0 | < константа> Ф 15 |

(< выражение >) Ф 0 | (< сравнение >) Ф 0

<сравнение> : : = < выражение > = < выражение > Ф 16 |

< выражение > ^ < выражение > Ф 17

X : : = < идент > Ф 18

< константа > : : = ЛОГ | ЦЕЛ

• < идент > : : = < буква > | < идент >< буква >

• < буква > : : = а | б | в | г .. .| я .

Функции Фi ( i = 1,...,18) на уровне видов:

Ф 0 = ( знач х ) знач : (ПРАВИД) ПРАВИД

Ф 1 = ( конт t , знач х , у ) конт : ( M mF , е, ПРАВИД) еmF

Ф 2 = ( конт t , знач х ) конт : ( E , M ) Ф 3( E , е, M )

Ф 3 = ( конт t , знач х, у ) конт : (( M ВИД X # E , е, ВИД⁽¹⁾ X # M ⁽¹⁾) ± | ( E , е , ВИД X # M ) Ф 3( имя ВИД X # E , е , M ) | ( E , е , е ) знач ( е ))

Ф 4 = ( знач х , у ) знач: (ПРАВИД, ПРАВИД⁽¹⁾) ПРАВИД⁽¹⁾

Ф 5 = ( знач х , текст у ) знач : (ВИД X # M , X ⁽¹⁾)ВИД X # M ВИД X ^<п #

Ф 6 = (текст х , у ) знач : (ВИД, X ) имя ВИД X #

Ф 7 = (знач х , у ) знач : ( имя ВИД, ВИД) имя ВИД

Ф 8 = (знач х , у ) знач : (лог ПРАВИД) ничто

Ф 9 = (знач х , у ) знач : ( (лог, ПРАВИД, ПРАВИД) ПРАВИД | (лог,

ПРАВИД, ПРАВИД⁽¹⁾) ничто) )

Ф 10 = Ф 8; Ф 11 = Ф 12 = Ф 0

Ф 13 = (знач х , у ) знач : ( (цел, цел) цел | (лог, лог) лог)

Ф 14 = Ф 13; Ф 15 = (текст х ) знач : ((ЦЕЛ) цел | (ЛОГ) лог )

Ф 16 = (знач х , у ) знач : (( ВИД , ВИД) лог) ; Ф 17 = Ф 16

Ф 18= (конт t , текст х ) знач : ( M ВИД X # E , X ) ВИД

Функции Фi ( i = 1,...,18) на уровне значений:

Ф 0 = ( знач х ) знач: (ПРАЗНАЧ) ПРАЗНАЧ

Ф 1 = ( конт t , знач х , у ) конт : ( M m F , е , ЗНАЧ) его F

Ф 2 = ( знач х ) знач : ( ВИД &  M ) M

Ф 3 = ( конт t , знач х , у ) конт, функ: ( M m F , M ⁰⁾, ВИД &  M ^<2))

MM⁽¹⁾M^<2)m F , знач ( е )

Ф 4 = ( знач х , у ) знач: (ПРАЗНАЧ, ПРАЗНАЧ⁽¹⁾) ПРАЗНАЧ⁽¹⁾

Ф 5 = ( знач х , текст у ) знач : (ВИД &  M , X ) r (ВИД, MX * 1# X 1*,

ВИД) ”

Ф 6 = (текст x , у ) знач : (ВИД, X ) r ( имя ВИД, X * 1# X 1*, ВИД) r = ((ВИД, MXH , имя ВИД⁽¹⁾ )

r (ВИД, MXH * eval ( H + 1)# Xeval ( H + 1)*,ВИД⁽¹⁾ )

| (ВИД, MXH ,ВИД⁽¹⁾ ) ВИД & MXH *неопр#)

Ф 7 = ( конт t , знач x , у ) конт : ( MXH * ЗНАЧ #M⁽¹⁾ F ,

XH , ЗНАЧ⁽¹⁾) MXH * ЗНАЧ⁽¹⁾ # M ⁽¹⁾ mF

Ф 8 = (знач x , функ у ) знач : ( (истина, у ) у ) | (ложь, у ) £ )

Ф 9 = ( знач x , функ у , z ) знач : (( истина, у , z ) у ) | (ложь, у , z ) z ); Ф 10 = ( функ x , у ) знач : ( x , у ) r 1 ( x , x , у )

r 1 = ( знач x , функ у , z ) знач : (( истина, у , z ) f 4 ( z , r 1 ( у , у , z )) | (ложь, у , z ,) ^£ ;

Ф 12 = (конт t , знач x ) конт: ( M mB § B ⁰⁾ ,ЗНАЧ) M mB § B ⁰⁾ * ЗНАЧ

Ф 13.1 = (знач x , у ) знач: (ЦЕЛ, ЦЕЛ⁽¹⁾) eval (ЦЕЛ+ЦЕЛ⁽¹⁾)

Ф 13.2 = (знач x , у ) знач: (( истина, ЛОГ) истина | (ложь, истина) истина | (ложь, ложь) ложь)

Ф 14.1 = (знач x , у ) знач : (ЦЕЛ, ЦЕЛ⁽¹⁾) eval (ЦЕЛ*ЦЕЛ⁽¹⁾)

Ф 14.2 = ( знач x , у ) знач : ( (ложь, ЛОГ) ложь | (ЛОГ, ложь) ложь

| (истина, истина) истина )

Ф 15 = (текст x ) знач : (ЗНАЧ) ЗНАЧ;

Ф 16= (( знач x , у ) знач : (ЦЕЛ, ЦЕЛ) истина | (ЦЕЛ, ЦЕЛ⁽¹⁾) ложь )

Ф 17 = (( знач x , у ) знач : (ЦЕЛ, ЦЕЛ) ложь (ЦЕЛ, ЦЕЛ⁽¹⁾) истина

| (ЛОГ, ЛОГ) ложь (ЛОГ+ЛОГ⁽¹⁾) истина)

Ф 18 = ( конт t , текст x ) знач : ( MX * ЗНАЧ § M⁰⁾mF , X )ЗНАЧ.

Заключение

В данной работе разработан подход к компьютерному моделированию динамических систем. Для этого был построен класс функций, являющийся алгебро-логической моделью языка программирования общего назначения. Тогда любая компьютерная программа, предназначенная для моделирования динамической системы, порождает моделирующий процесс. При данном подходе указанная программа представляется в виде алгебраического выражения (терма) универсальной алгебры, являющейся семантикой языка программирования. Имея терм для моделирования динамической системы, можно сформулировать и математически корректно доказать те или иные теоремы о процессах моделирования.