Об одном подходе к решению трансцендентных уравнений
Автор: Шийдэв Б., Очирбат Б., Бутуханова Д.В.
Журнал: Вестник Бурятского государственного университета. Философия @vestnik-bsu
Рубрика: Теория и методика обучения естественно-математическим дисциплинам
Статья в выпуске: 15, 2009 года.
Бесплатный доступ
В статье предлагается метод приближенного решения трансцендентных уравнений на примере анализа известного уравнения из области высшей математики.
Трансцендентное уравнение, производная, касательная прямая
Короткий адрес: https://sciup.org/148178688
IDR: 148178688 | УДК: 510.1
Текст научной статьи Об одном подходе к решению трансцендентных уравнений
Решим одно простое уравнение lg x = x — 1 , которое нередко встречается в разных учебниках и учебных пособиях элементарной математики .
Ясно, что x = 1 является корнем данного уравнения. Возникают вопросы: Есть ли другой корень, если есть, то где он находится, как найти его приближенное значение с заданной точностью и.т.д
Для того, чтобы ответить на данные вопросы исспользуем понятия о производной. Сначала напишим уравнение касательной к графику функции у = lg x в точке с абсциссой x0 = 1 .
Так как x 0 = 1 , то у 0 = lg1 = 0 . С другой стороны у ' =------ . Следовательно угловой
0 x • ln10
коэффициент касательной к = у '| , = —-—| = —-— = lg e .
x 0 = 1 x ln10 x 0 = 1 ln10
Отсюда уравнение касательной к кривой у = lg x в точке x 0 = 1 имеет вид у = lg e • ( x — 1 ) и она не совпадает с прямой у = x — 1 . Это означает, что прямая у = x — 1 пересекает кривую у = lg x в точке, отличной от точки ( 1;0 ) , иными словами уравнение lg x = x — 1 имеют два корня.
Так как угловой коэффициент прямой у = x — 1 имеет к1 = 1 , а для прямой у = lg e • ( x — 1 ) имеет к 2 = lg e и lg e < 1 , то к 2 < k 1 . Отсюда следует, что касательная у = lg e • ( x — 1 ) образует угол с положительным направлением оси Ох меньше 45 o (рис 1). Следовательно, уравнение lg x = x — 1 имеет второй корень в интервале ( 0;1 ) .
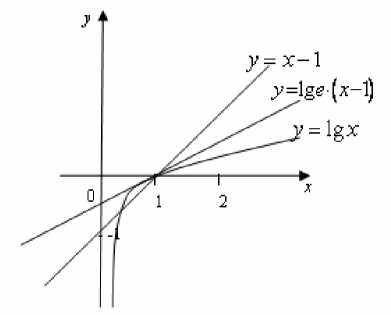
Рис. 1.
Работа выполнена при финансовой поддержке РФФИ (проекты 08-01-00945-а, 09-01-90203-Монг-а),
РГНФ (проект 09-02-00493-а).
Теперь найдем приблаженное значение этого корня.
Возьмем функцию f ( x ) = lg x — x + 1 .
Так как f' (x) =------- x • ln10
. lg e . lg e — x
1 = —-- 1 = —---- , то из уравнения f ' ( x ) = 0 имеем x = lg e и она
x
x
есть точка локального максимума, так как при 0 < x < lg e имеем f ' ( x ) > 0 , а при lg e < x < 1 имеем f ' ( x ) < 0 , причем у max = f ( lg e ) = lg e lg e — lg e + 1 = lg 10 lg e > 0.
e lg e
Кроме этого данная функция является выпуклой в промежутке ( 0;1 ) , так как f " ( x ) =--2- < 0
x2
x
-^ ,
С другой стороны lim f ( x ) = lim ( lg x — x + 1 ) = lim lg---— x i+^ x i+^ v ' x i+^ 10 x 1
x lin+0 f (x ) = xlim0 (lg x — x +1) = —^ и lg e < 2 . Отсюда можно изобразать эскиз графика данной функции следующим образам (рис 2).
.
Пусть, например x 1 = — и x 2 = —
Так как f (x1 ) = f
11 1
----+ 1 =--< 0, 10 10 10
f ( x 2 ) = f
2 2 1
---+1 = lg2 — - = lg
10 10 5
> 0,
то второй корень а уравнения lg x = x — 1 заключается в промежутке
1 2 )
; . Если проведем
10 10 )
прямую через точки
M 1
10 10
и M 2
, то
уравнение примет вид
x--
10 10
10 a — 1 =
1 у +—
lg2 — - +—
5 10
л 10 У + 1
или 10 x — 1 =-------- . Подставляя x = а и
10 lg 2 — 1
у = 0 , получим равенство
10lg2 — 1 a - 0,14975 - 0,15 .
и
lg2
отсюда а =--------
10 • lg2 — 1
.
Учитывая, что
lg 2 - 0,3010 , получим
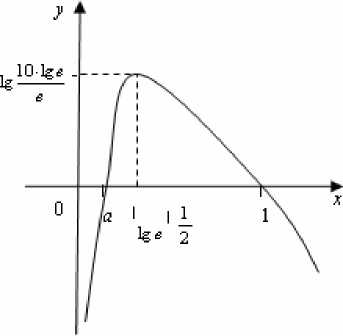
Рис. 2.
Таким образом, уравнение lg x = x — 1 имеют два корня x 0 = 1 и x - 0,15
Заключение
Предлагаемая процедура решения трансцендентных уравнений является одним из основных методов и охватывает большой круг подобных задач.
Б . Шийдэв, прфессор, Технологический институт имени Ш.Отгонбилега
Россия, 670000, Улан-Удэ, ул. Смолина, 24а, тел. (3012)219757


