Об одном подходе к сравнению нечетких чисел

Автор: Ухоботов Виктор Иванович, Щичко Павел Владимирович

Журнал: Вестник Южно-Уральского государственного университета. Серия: Математическое моделирование и программирование @vestnik-susu-mmp

Рубрика: Математическое моделирование

Статья в выпуске: 37 (254), 2011 года.

Бесплатный доступ

В статье предложен метод сравнения двух нечетких чисел, основанный на сравнении их множеств уровня.

Нечеткие множества, сравнение нечетких чисел

Короткий адрес: https://sciup.org/147159112

IDR: 147159112

Текст научной статьи Об одном подходе к сравнению нечетких чисел

При решении задач принятия решения в условиях нечеткой информации довольно часто возникает потребность в сравнении нечетких чисел. Следующая задача иллюстрирует данную необходимость.

Вкладчик, имея валюту в объеме N , выбирает один из двух валютных вкладов с ki процентной ставкой, i = 1, 2. Курс i-й валюты по отношению к базовой на момент вклада равен ri . На момент окончания вклада он будет равен Ri , точное значение которого не известно. По окончанию срока вклада в базовой валюте вкладчик получит сумму xi = (1 + ki)yN, у = Ri, i = 1, 2. ri

C помощью экспертной оценки построен прогноз значения отношения Ri в виде нечетко-ri го множества [1]. Это значит, что построены функции vi : R ^ [0,1], значение vi(y) каждого из которых для числа y G R задают меру того, что отношение Ri = у.

Таким образом, сумма, которая будет на счету у вкладчика, характеризуется функцией ^ i ( x ) = V i ( n (l+k i ) ). Величина ^ i ( x ) задает меру того, что на счету у вкладчика будет сумма x . Вкладчик, выбирая вид валютного вклада, имеет цель сделать сумму x , как можно больше. Следовательно, для решения задачи нам необходимо произвести сравнение нечетких чисел ^ i ( x ).

Нечетким числом называется нечеткое множество [1], универсальным множеством которого является множество действительных чисел R . Нечеткое число X однозначно определяется своей функцией принадлежности ^ : R ^ [0 , 1]. Для конкретного действительного числа x G R значение ^ ( x ) задает степень принадлежности x нечеткому множеству X .

Зафиксируем число 0 < a < 1. Пусть лицо принимающее решение игнорирует появление тех значений x G R критерия, для которых ^ ( x ) < a . Тогда он принимает во внимание только возможные значения x G X ( a ), где

X ( a ) = { x G R : ^ ( x ) > a } .

Множества (1) называются множествами уровня нечеткого числа X .

Будем рассматривать нечеткие числа, у которых множества уровня являются отрезками

X ( a ) =

J [ g ( a ) , G ( a )] при 0 < a < f < 1

[ 0 при f < a < 1

0 < 1 .

Это выполнено, например, для LR -нечетких чисел [2].

В работе [3] дается обзор различных подходов к сравнению нечетких чисел. В работе [4] для каждого нечеткого числа X , у которого f = 1, строится оценка

Val(X ) = 2

J (g(a) + G(a))p(a)da 0

p ( a ) da

По этим оценкам сравниваются нечеткие числа.

1. Описание метода

Рассмотрим два нечетких числа X i , множества уровня X i ( a ) которых задаются формулой (2). Относительно функций g i ( a ) < G i ( a ) предположим, что они удовлетворяют условиям:

0 < a i < a 2 < f i = ^ g i (a i ) < g i ( a 2 ) , G i ( a i ) < G i (a 2 ) , (4)

inf g i (a) = a i > —to , sup G i (a) = e i < + to . (5)

⁰ ^<α ^≤ ^f i 0 <αi

Как отмечалось во введении, если лицо, принимающее решение игнорирует те значения x , для которых ^ i ( x ) < a , i = 1 , 2, то он должен сравнивать отрезки (2). Естественно считать, что при выборе отрезка [ g i ( a ) , G i ( a )] ожидаемое среднее значение x критерия равно середине отрезка, а отклонение возможной реализации критерия от этого среднего можно оценивать длинной этого отрезка. Чтобы уменьшить риск большого отклонения возможной реализации критерия от середины отрезка применим критерий математического ожидания – дисперсии [5]

^ i ( a ) = g i ( a ) + G i ( a ) - A(G i ( a ) - g i ( a )) ^ max , i = 1 , 2 . (6)

Здесь число A > 0 характеризует субъективное отношение лица, принимающего решение к риску.

Доопределим, что ^ i ( a ) = -то при f i < a < 1, i = 1 , 2. Обозначим

J ik = { a G (0 , 1] : ^ i ( a ) > ^ k ( a ) } , f ik = min f f k ) .

Задана функция p : [0 , 1] ^ [0 , 1], которая характеризует меру важности степени уровня a G (0 , 1] с точки зрения лица принимающего решение.

Определение 1. Будем говорить, что нечеткое число X i не хуже нечеткого числа X _k , если

P ik ≥ P ki ,

J p(a)da, если J ik = 0 где P ik = J ik

P ik = 0 , если J ik = 0 .

Существование интеграла в (8) предполагаем.

2. Случай трапецеидальных нечетких чисел

График функции принадлежности трапецеидального нечеткого числа [6] приведен на риc. 1.

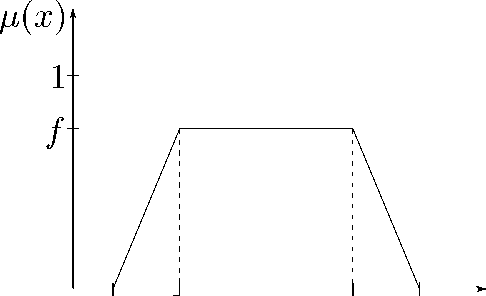
a b c e x

Рис. 1

Очевидно, что условия (2), (4), (5) выполнены. Далее,

g(a^ = a

b - a

G ( a ) = e — a—-—

при 0 < a < f,

поэтому при A > 0 функция (6) примет вид

_V ( a ) = (1 + A ) a + (1 — A ) e + ^{(1 +} ^A ⁾⁽ b - a) ^— ⁽¹ - ^’( e — , 0 < a < f. (9)

Обозначим:

ε i	b i - a i b k - a k e i - c i e k - c k ^k = ^{(1 +} ^A4 f i f k ) ⁽¹ ^A)( f . ' f k )' (10)

5 ik = (1 + A )( a i — a k ) + (1 — A )( e i — e k ) .

Из формул (10) и (7) следуют равенства:

^ ik ^ ki , ^ ik ^ ki , f ik f ki - ⁽¹¹⁾

Формула (7) принимает вид:

Обозначим:

J ik = ^{ ^a ^Е ⁽⁰ ^, f ik ^] : § ik ⁺ ^a E ik > ⁰ ^{} U} ⁽ ^f k , ^1] - ⁽¹²⁾

P = j p(r)dr. (13)

Предложение 1. Пусть заданы числа a,b Е (0; 1]. Тогда для множества J =

(0, min(a, b)] U (b, 1] верно равенство j p(r)dr = min

Доказательство. Пусть a < b < 1. Тогда J = (0 , a ] U ( b, 1]. Следовательно:

b j p(r)dr = P — У p(r)dr = min

Пусть b < a < 1. Тогда J = (0 , b] U ( b, 1] = (0 , 1]. Следовательно:

( a \ / b

P; P + / p(r)dr I = min P; P — / p(r)dr ba

Вычислим значения чисел P ik и P ki (8) при разных значениях чисел ε ik и δ ik .

1. Пусть 6 ik = 0 и E ik = 0. Тогда, согласно равенствам (11), b ki = 0 и E ki = 0. Из формулы (12) получим, что J ik = (0 , f ik ] U ( f k , 1], J ki = (0 , f k ] U (f i , 1]. Отсюда, используя равенство f ik = f ki = min( f ; f k ) и утверждения 1, получим, что

P ik = min

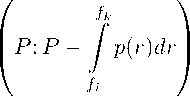
P ki = min

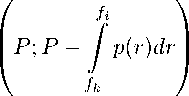
Следовательно:

P ik = P, P ki = P — J p(r)dr, при f k < f i ;

P ik = P - / p ( r ) dr, P ki = P, при f i < f k .

2. Пусть 6 ik = 0 и E ik > 0. Тогда 6 ki = 0 и E ki < 0. Из формулы (12) следует, что: J ik = (0 , f i ] U ( f k , 1] и J ki = ( f i , 1]. Следовательно, P ik задается первой формулой из f i
3. Пусть 6 ik = 0 и E ik < 0. Тогда 6 ki = 0 и E ki > 0. Согласно предыдущему пункту

(15), а P ki = P — Jp(r)dr. Стало быть,

P ik = P, P ki = P - /p ( r ) dr, при f k < f i ;

P ik = P - J p ( r ) dr, P ki = P - J i p ( r ) dr, при f i < f k .

P ik = P - J p(r)dr, P ki = P - J i p(r)dr, при f k < f i ;

P ki = P - J p(r)dr, P ki = P, при f i < f k .

4. Пусть S ik > 0 и S ik + f ik E ik > 0. Тогда J i_k = (0 , f ik ] U ( f k , 1], J ki = ( f i , 1]. Из предложения

1 получим, что:

( f k \ 1

P ; P - jp(r)dr I , P ki = jp(r)dr.

fi fi

Раскрывая первую формулу, получим

P ik = P, P ki = P - Jp(r)dr, при f k < f i ;

P ik = P — J p ( r ) dr, P ki = P — J i p ( r ) dr, при f i < f k .

5. Пусть 6 ik > 0 и 6 ik + f ik E ik < 0. В этом случае
6. Пусть 6 ik < 0 и 6 ik + f ik E ik > 0. Тогда S ki > 0 и S ki + f ki E ki < 0. Согласно формулам

7. Пусть

0 и

0. Тогда

0 и

0. Тогда из формулы (19)

J ik = Г⁰ ^, ] ^U ⁽ ^f k 1 ^1] , J ki = [ , ^f k ] ^U ⁽ ^f i , ^1] • ^ε ik ^ε ik

Раскрывая последнюю формулу, получим

_- δ_ik ε_ik	1	k 1
P ik = / p ( r ) dr	+ p ( r ) dr,	P ki = / p ( r ) dr + Jp(r)dr, при f k < f i ;
0	k	_- ^δik i
_- δ_ik		^εik (20)
^εik	1	1
P ik = p ( r ) dr	+ p ( r ) dr,	P ki = j p(r)dr, при f i < f k •
0	k	_- δ_ik ε_ik

	_- ^δik
1	^εik 1
P ik = j p(r)dr	P ki = / p ( r ) dr + / p ( r ) dr, при f k < f i ;
- ⁵ik	0 i
^εik	_- δ_ik	(21)
i	1 ^εik 1
P ik = p ( r ) dr	+ / p ( r ) dr, P ki = / p ( r ) dr + / p ( r ) dr, при f i < f k •
_— ^Sik ^εik	k 0 i

получим, что fk fi

P ik = P - J p ( r ) dr, P ki = P - J p(r)dr, при f k < f i ;

P ik = P - J p(r)dr, P ki = P, при f i < f k •

Полученные формулы (16) - (22) для случаев 0 < f2 < f 1 и 0 < f2 = fi приведены в таблицах 1 и 2.

Таблица 1

Результаты сравнения при f 2 < f 1

0 < f 2 < f 1

5 12 < 0

⁵ 12 = ⁰

5 12 > 0

⁵ 12 + ^f 2 ^E 12 < ⁰

P 21 < P 12 ^^

f 2 f 1

J p(r)dr < Jp(r)dr 0 f 2

P 21 < P 12 ^^

f 2 f 1

p ( r ) dr < p ( r ) dr

0 f 2

P 21 < P 12 ^^

f 2

J p(r)dr <

^δ 12

^ε 12

- ^δ ¹²

^ε 12

J p(r)dr +

f 1 p ( r ) dr

f 2

5 12 + f 2 E 12 = 0

P 21 < P 12 ^^

f 2 f 1

J p(r)dr < J p(r)dr 0 f 2

P 21 < P 12 ^^

f 1

p ( r ) dr > 0

f 2

P 21 < P 12 ^^

f 1

p ( r ) dr > 0

5 12 ⁺ ^f 2 ^E 12 > ⁰

P 21 < P 12 ^^

- ^δ ¹²

^ε 12

p ( r ) dr <

0 f 1 p ( r ) dr

- ^δ ¹²

^ε 12

P 21 < P 12 ^^

f 1

p ( r ) dr > 0

P 21 < P 12 ^^

f 1

p ( r ) dr > 0

Таблица 2

Результаты сравнения при / 2 = / 1 = f

f 2 = f 1 = f	5 12 < 0	⁵ 12 = ⁰	5 12 > 0
⁵ 12 ⁺ ^f E 12 < ⁰	P 21 > P 12	P 21 > P 12	P 21 < P 12 ^^ _- δ ₁₂ ε ₁₂ 2 p ( r ) dr > 0 f Jp(r)dr 0
5 12 + fE 12 = 0	P 21 ^> P 12	P 21 = P 12	P 21 ^< P 12
⁵ 12 ⁺ f^E 12 > ⁰	P 21 < P 12 ^^ _- ^δ 12 ^ε 12 2 J p(r)dr < 0 f p ( r ) dr 0	P 21 < P 12	P 21 < P 12

Возьмем p ( r ) = mr m 1 , m > 1. Тогда таблицы 1 и 2 примут вид таблиц 3 и 4.

Результаты сравнения при f 2 < f i , p ( r ) = mr m ¹

Таблица 3

0 < f 2 < f i	^ i2 < 0	^ .2 = ⁰	^ i2 > 0
^ i2 ⁺ ^f 2 ^E i2 < ⁰	P 2i < P i2 ²² 2 f 2 m < f i m	P 2i < P i2 ²² 2 f 2 m < f i m	P 2i < P i2 "=^ 2 f 2m - ² (- fit)’” < f 1 ^m
^ i2 ⁺ ^f 2 ^E i2 = ⁰	P 2i < P i2 ²² 2 f 2 m < f i m	P 21 < P 12	P 21 < P 12
^ i2 ⁺ ^f 2 ^E i2 > ⁰	P 2i < P i2 ²² ² (- ■ Г i m	P 21 < P 12	P 21 < P 12

Таблица 4

Результаты сравнения при f 2 = f 1 = f , p ( r ) = mr ^m ^- ¹

f 2 = f i = f	^ i2 < 0	^ i2 = ⁰	^ i2 > 0
^ i2 + fE i2 < 0	P 21 > P 12	P 21 > P 12	P 2i < P i2 ^^ ²( - l ik )" ‘>f m
^ i2 + fE i2 = 0	P 21 > P 12	P 2i = P i2	P 21 < P 12
^ i2 + fE i2 > 0	P 2i < P i2 ^^ ² (- f ik У m	P 21 ^< P 12	P 21 ^< P 12

Рассмотрим случай, когда эксперт хочет учитывать только значения а близкие к 1, то есть случай m ^ го . Этот случай отображен в таблице 5. Отметим, что в случае f 2 < f i нечеткое число с меньшей высотой будет всегда меньше нечеткого числа с большей высотой.

Таблица 5

Результаты сравнения при f 2 = f i = f , p(r) = mr m 1 , m ^ го

f 2 = f i = f	^ i2 < 0	^ i2 = ⁰	^ i2 > 0
^ i2 ⁺ ^fE i2 < ⁰	P 21 > P 12	P 21 > P 12	P 21 < P 12
^ i2 + fE i2 = 0	P 21 > P 12	P 2i = P i2	P 21 < P 12
^ i2 + fE i2 > 0	P 21 ^< P 12	P 21 ^< P 12	P 21 ^< P 12

Обозначим в = y+ j . Тогда имеем

^12 = (1 + A)(ai — a2 + в(ei - e2)), bi - ai b2 - a2 «ei — ci , «62 — c2\

^E ⁱ² = ⁽¹⁺ ^A)( и IT ^- ■ ⁺ ^в^гУ

Для A = 0 получим

b i - a i b 2 - a 2 e i - c i e 2 - c 2

^E ⁱ² =V f i ' f 2 ' f i ' f 2 )'

^ i2 = ( a i - a 2 + e i - 6 2 ) -

В соответствии с этим, мы можем переписать условия для сравнений. Они приведены в таблицах 6 и 7.

Таблица 6

Результаты сравнения при / 2 < f i , p ( r ) = mr m 1 , m ^ го , A = 0

0 < f 2 < f 1	a i + e i < a 2 + e 2	a i + e i = a 2 + e 2	a i + e i > a 2 + e 2
(1 - f l ) ⁽ a i ⁺ e i ) ⁺ f l ( b i + c i ) 2 + C 2	P 21 < P 12	P 21 < P 12	P 21 < P 12
(1 - f l ) ⁽ a i ⁺ e i ) ⁺ f l ( b i + c i ) 2 + c 2	P 21 < P 12	P 21 < P 12	P 21 < P 12
(1 - f l ) ⁽ a i ⁺ e i ) ⁺ f l ( b i + c i ) 2 + c 2	P 21 < P 12	P 21 < P 12	P 21 < P 12

Таблица 7

Результаты сравнения при / 2 = f i = f , p(r) = mr m 1 , m ^ го , A = 0

f 2 = f i = f	a i + e i < a 2 + e 2	a i + e i = a 2 + e 2	a i + e i > a 2 + e 2
b i + c i 2 + c 2	P 21 > P 12	P 21 > P 12	P 21 > P 12
b i + c i = b 2 + c 2	P 21 > P 12	P 2i = P i2	P 21 < P 12
b i + c i > b 2 + c 2	P 21 ^< P 12	P 21 ^< P 12	P 21 ^< P 12

Из таблицы 7 видно, что в случае равенства высот, сначала нужно провести сравнение Xi по ядру core Xi = [bi, ci]. Затем, в случае равенства, сравнение нужно провести по носителю suppXi = [ai,ei]. Другими словами, необходимо найти оптимальное в лексикографическом смысле решение двухкритериальной задачи bi + ci ^ max, ai + ei ^ max, i = 1, 2.

Список литературы Об одном подходе к сравнению нечетких чисел

Заде, Л. Понятие лингвистической переменной и его применение к принятию приближенных решений/Л. Заде. -М.: Мир, 1976.
Дюбуа, Д. Теория возможностей. Приложения к представлению знаний в информатике/Д. Дюбуа, А. Прад. -М.: Радио и связь, 1990.
Chen, S. Fuzzy multiple attribute decision making methods and applications/S. Chen, С Hwang. -N. Y.: Springer, 1992.
Yager, R.R. On ranking fuzzy numbers using valuations/R. R. Yager, D. Filev//International J. of Intelligent Systems. -1999. -V. 14, №. 12. -P. 1249 -1268.
Ухоботов, В.И. Математика. Экономико-математические методы и модели/В.И. Ухоботов, А.Н. Тырсин, С.А. Никитина. -Челябинск: Изд-во Челяб. гос. ун-та, 2010.
Ухоботов, В.И. Введение в теорию нечетких множеств и ее приложения/В. Ухоботов. -Челябинск: УрСЭИ AT и СО, 2005.
Zade L. Linguistic variable and its appliance in theory of approximate solutions [Ponyatie lingvisticheskoy peremennoy i ego primenenie k prinyatiyu priblizhennykh resheniy]. Moscow, Mir, 1976.
Dyubua D. and Prad A. Possibility theory. Appliances to representation knowledge in informatics [Teoriya vozmozhnostey. Prilozheniya k predstavleniyu znaniy v informatike]. Moscow, Radio i svyaz', 1990.
Chen S. and Hwang C. Fuzzy multiple attribute decision making methods and applications. N. Y., Springer, 1992.
Yager R.R. and Filev D. On ranking fuzzy numbers using valuations. International J. of Intelligent Systems. 1999, vol. 14, no. 12., pp. 1249 -1268.
Ukhobotov V.I., Tyrsin A.N, and Nikitina S.A. Mathematics. Economic and mathematical methods and models [Matematika. Ekonomiko-matematicheskie metody i modeli]. Chelyabinsk, Izd-vo Chelyab. gos. un-ta, 2010.
Ukhobotov V.I. Introduction into fuzzy set theory and its appliances [Vvedenie v teoriyu nechetkikh mnozhestv i ее prilozheniya]. Chelyabinsk, UrSEI AT i SO, 2005.

Еще

Статья научная