Об одном подходе к сравнению нечетких чисел в задачах принятия решений

Для целого класса экономических и социальных задач информация о переменных носит нечеткий расплывчатый характер. Для исследования таких задач используются нечеткие числа. С момента опубликования Л. Заде своей работы по нечетким множествам [1], вышло большое количество работ, в которых рассматриваются действия с нечеткими числами [2, 3].

В задачах принятия решения, когда лицо, принимающее решение, в зависимости от выбранной им стратегии получает информацию о реализации этой стратегии в виде нечеткого числа, возникает проблема сравнения нечетких чисел.

К настоящему времени предложено достаточное количество различных методов сравнения нечетких чисел [4]. Ни один из них не является универсальным. Возникает проблема с интерпретацией тех или иных методов, не все они понятны интуитивно.

При решении прикладных задач в вопросах принятия решений при выборе того или иного метода сравнения нечетких чисел нужно исходить из специфики задачи.

В данной работе продолжаются исследования, начатые в работе [5].

Постановка задачи

Пусть задана функция и A : R ^ [0;1]. Нечетким числом A называется [1] совокупность пар вида ( x | и A ( x ) ) , x e R . Функция и A ( x ) называется функцией принадлежности нечеткого числа A , а её значение на конкретном числе x e R называется степенью (или мерой) принадлежности этого числа x нечеткому числу A .

Для каждого числа a e [ 0;1 ] обычное множество A ( a ) = { x e R : и A ( x ) >  a } называется множеством уровня нечеткого числа A . Эти множества уровня удовлетворяют следующим свойствам:

A (0) = X ;0 <  а <  в <  1 ^ A ( в ) c A ( a ); 0 <  a < 1 ^ Q A ( t ) = A ( a ).      (1)

0 < t

Пусть при каждом 0 <  a <  1 определено множество A ( a ) c R . Если совокупность этих множеств удовлетворяет свойствам (1), то оно является семейством множеств уровня нечеткого числа A , функция принадлежности которого равна

^ _A ( x ) = sup { a e [0;1]: x e A ( a ) } .

Поэтому нечеткое число A можно задать семейством множеств A ( a ) c R , при каждом 0 <  a <  1, удовлетворяющих свойствам (1).

В данной работе будем рассматривать нечеткие числа, множества уровня которых имеют вид отрезков [6]

A ( a ) = [ a + £ f ( a ); b - 5ф ( a )].

Функции f , ^ :(0;1] ^ ( -^ ;0] и коэффициенты a, £ ,b, 5 удовлетворяют следующим свойствам:

0 <  a 1 < a 2 <  1 ^ f ( a 1 ) <  f ( a ₂ ), ^1) < ^ 0 2 ); f (1) = ^ (1) = 0;

lim f ( t ) = f (t ), lim ^ ( t ) = ^ ( t ) , £ >  0, 5 >  0, a <  b . t ^t - 0               t ^t - 0

При выполнении условий (3) отрезки (2) удовлетворяют свойствам (1).

Пусть лицо, принимающее решение (ЛПР), может выбрать одну из двух стратегий. Цель ЛПР заключается в том, чтобы выигрыш x е R , который он получит при выборе i- й стратегии, был как можно больше. Однако информацию о возможном результате он получает в виде нечеткого числа A_i .

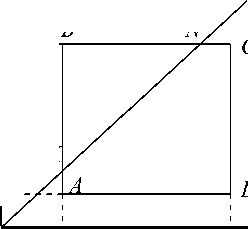
Зафиксируем число 0 <  a <  1 и будем считать, что ЛПР интересует только те выигрыши, значения которых x е A i ( a ), i = 1,2. Приходим к задаче о сравнении отрезков [ g 1 ( a ); G 1 ( a ) ] и [ g₂( a ); G₂( a ) ] . Вид функций g i ( a ) и G i ( a ) следует из формулы (2). На плоскости z 1 Oz ₂рассмотрим прямоугольник ABCD (см. рис.1). На этом рисунке прямая ON является множеством точек ( z 1 , z ₂ ) , у которых z । = z ₂. Считаем, что отрезок [ g i ( a ); G i ( a ) ] предпочтительнее для ЛПР отрез-

ка |^ g j ( a ); G j ( a ) J тогда и только тогда, когда площадь фигуры AKNCD не меньше площади фигуры KBN .

Этим определением мы формализуем тот факт, что «число» пар ( z 1 , z ₂ ) выигрышей z 1 е [ g i ( a ), G i ( a ) ] и z ₂ е |^ g j ( a ), G j ( a ) J , у которых z 1 >  z ₂ не меньше, чем число пар выигрышей, у которых z 1 <  z ₂ .

Нетрудно показать, что [7] площадь фигуры AKNCD не меньше площади фигуры KBN тогда и только тогда, когда

Z 2

g i ( a ) + G i ( a ) >  g j ( a ) + G j ( a ).

Последнее неравенство означает, что середина i -го отрезка не меньше середины j- го отрезка.

B

K gj "

G j

O    g i

G i      z 1

Рис. 1. Задача о сравнении отрезков

Обобщим изложенный подход. С этой целью зафиксируем число 0 <  2 <  1 и рассмотрим величину

Q i ( a ) = (1 - 2 ) ( g i ( a ) + G ( a ) ) + 2 ( g i ( a ) - G ( a ) ) .

Выбор наибольшего из двух чисел Q i ( a ) и Q j ( a ) отражает намерение ЛПР выбрать отрезок, у которого, по возможности, больше середина и меньше длина. Сравнение нечетких чисел A i и A j будем проводить с помощью неравенства

Q ( a ) >  Q j ( a ).

Слабая предпочтительность нечетких чисел

Определение 1 . Будем говорить, что нечеткое число A i предпочтительней нечеткого числа A j в слабом смысле, если существует число 0 <  у <  1 такое, что неравенство (5) выполнено при всех у <  a <  1.

Пример 1. Функция принадлежности нечеткого числа A = «примерно b или более» может быть задана следующей формулой:

r

z х 1 , Д ( x ) = - 1 - exp

-

γ

V

V

x

ε

при 0 <  x <  b , ^ ( x ) = exp

( ( x - b ^v ' )

-

V V 5 7 J

-

при b <  x ; у = 1 — e

V

2 A

. (6)

График этой функции приведен на рис. 2. Множества уровня этого нечеткого числа являются отрезками [ g ( a ); G ( a )] с функциями

Математика

g ( a ) = e^ - ln ( 1 - ay ) , G ( a ) = b + S V - ln a .

Поэтому функция (4) равна

Q( a ) = E - ln ( 1 - aY ) + (1 - 2 2 ) ( b + S - In a ) .

Обозначим

I ------------- 2

t = V- In a ^ a = e~t ,0 <  t <+^ ; a ^ 1 ^ t ^ 0.

Тогда множество

D ⁽ t ) = Q ( ^exP^{( -} t ²⁾ )

равно

D ( t ) = E - In ( 1 - y + (1 - exp ( - t ² ) ) y ) + (1 - 2 2 ) ( b + S t ) .

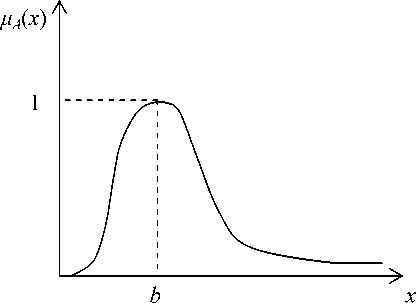
Рис. 2. График функции принадлежности «примерно b и не более»

Разлагая это выражения по степеням t и используя вид числа у(6), получим

D ( t ) = b

(

V

г

£г

⁺ ^    ¹ ’^exp

V

b |

I E ' )

^ t ² ,

+ (1 - 2 2 ) ( b + S t ) + o ( t ²) .

Запишем неравенство (5) в виде

D i ( t ) >  D j ( t ) при малых t > 0.                                (8)

Из формулы (7) получим, что, если bi > bj, то (8) будет выполнено. Пусть bi = bj = b. Тогда, если S > S, то (8) выполнено. Пусть bi = bj = b, S = Sj = S. Тогда (8) будет выполнено, если eT -1 ej -1    (b У

------<------ T = I — I .

T      ^T j      V ^E )

Поскольку функция ---- возрастает при т > 0, то предыдущее неравенство выполнено тогда и

τ только тогда, когда Ei > Ej. Если Ei = Ej, то, как следует из формулы (6), нечеткие числа Ai и Aj- совпадают.

В общем случае анализ слабой предпочтительности нечетких чисел можно проводить с помощью разложения в степенные ряды функции принадлежности.

Из формул (2) и (4) следует, что неравенство (5) равносильно следующему неравенству: E i f i ( a ) - E f ( a ) + (1 - 2 2 )( S j P j ( a ) - Sp i ( a )) >  a j - a , + (1 - 2 2 )( b j - b i ).              (9)

Из формулы (9) и из условий f_S (1) = p _S (1) = 0 следует, что, если a i + (1 - 2 2 ) b i > a j + (1 - 2 2 ) b j ,                          (10)

то нечеткое число A i предпочтительнее в слабом смысле нечеткого числа A j .

Рассмотрим случай, когда в формуле (10) стоит равенство. Будем предполагать, что функции fS (a) и pS (a) представимы рядом Тейлора г \ v (a-1) нкл\ v (a-1) fs (a) = E   , /fs k) (1)’ Ps (a) = E   , / pk) (1) • k=1 k•                           k=1    k•

Подставим эти формулы в (9). Получим:

f s ( a ) = E ^ O J2 1 ( g f (^k ) (1) - e j f j ^k ) (1) + (1 - 2 2 ) ( Sp ) (1) - S i p k ) (1) ) ) >  0. k = 1 k !

Отсюда видно, что если

E i f i ‘ (1) - (1 - 2 2 ) Sp ‘ (1) <  E j f j (1) - (1 - 2 2 ) S_]p'_] (1),                         (11)

то найдется число 0 <  Y <  1, такое, что неравенство (9) будет выполнено при всех Y <  a <  1.

Если в неравенстве (11) стоит знак равенства, то рассмотрим следующие слагаемые и так далее.

Таким образом, задача сводится к нахождению оптимального в лексикографическом смысле решения многокритериальной задачи ai + (1 - 22)bi ^ max, (-1)k (eifi(k) (1) - (1 - 22)Sp(k) (1)) ^ max, i = 1,2.     (12)

Пример 2. Рассмотрим случай трапецеидальных чисел (см. рис. 3). Их лингвистическое описание имеет вид A = «примерно в интервале [ a , b ], но не менее a -e и не более b+ S »

Формула (2) примет вид:

A ( а ) = [ a + ( а - 1) e ; b - ( а - 1) S ], 0 <  а <  1.

В этом примере   fS (1) = фS (1) = а -1,   при s = 1, 2. Поэтому   fS (1) = p'S (1) = 1, fSk) (1) = Psk) (1) = 0 , k > 2 . Задача (9) примет вид ai + (1 -22)bi ^max, -ei + (1 -22)Si ^max, i = 1,2.                    (13)

В случае 2 = 0 задачу (13) запишем в виде ai + bi ^ max, - ei + Si ^ max, i = 1,2.

Допустим, что нечеткое число A i предпочтительнее A , но a i + b i = a j - + b j . Тогда из второго критерия получим, что S i - e i >  S j - e j . Как видно из рис. 3, разность S _S - e _S равна разности Q s^^ - Q S¹ площадей треугольников.

Таким образом, если середины отрезков, являющиеся ядрами нечетких чисел A i и A j [7], совпадают, то предпочтительней из них в слабом смысле то, у которых разность Q ^²^ - Q S¹ больше.

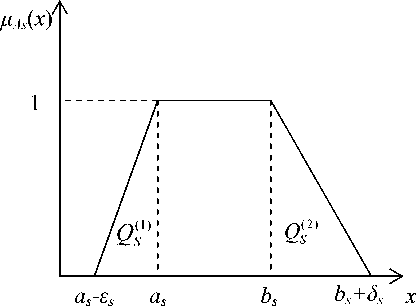
Рис. 3. К иллюстрации оптимальности в лексикографическом смысле

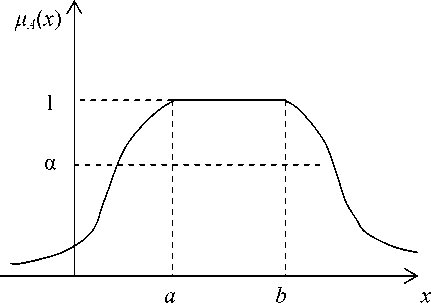
Рис. 4. График функции принадлежности колоколообразного числа

Сильная предпочтительность нечетких чисел

Определение 2. Будем говорить, что нечеткое число A i предпочтительней нечеткого числа A j в сильном смысле, если неравенство (5) выполнено при всех 0 <  а <  1.

Рассмотрим случай, когда fS (а) = pS (а) = ^(а), s = 1,2. Функция ^:(0;1] ^ (-~;0] не убывает и ^(1) = 0. Обозначим t = ^(а) и t* = lim ^(а).(14)

а ^ 0

Тогда неравенство (9) можно записать в следующем виде:

((ei - ej) - (1 - 22)(S - Sj)) t + ai - aj- + (1 - 22)(bi - bj) > 0 при t < 0.(15)

Случай t* = -^. Тогда неравенство (15) выполнено при всех t < 0 в том и только том случае, когда выполнено неравенство (10) и ei- (1 - 22)S< ej - (1 - 22)Sj .(16)

Случай t * > -^ . В этом случае неравенство (15) выполнено при всех t * <  t <  0 тогда и только тогда, когда выполнено неравенство (10) и

(ei - (1 - 22)S)) t* + ai + (1 - 22)bi > (ej - (1 - 22)Sj) t* + aj + (1 - 22)bj .(17)

Пример 3. Рассмотрим случай колоколообразных нечетких чисел A , у которых функция принадлежности имеет вид (см. рис. 4):

Математика

µ _A ( x ) = exp

к

x -

ε

при x ≤ a ; µ A ( x ) = 1 при a ≤ x ≤ b ;

µ _A ( x ) = exp

к

x - b δ

при b ≤ x .

Здесь числа a ≤ b,ε> 0,δ> 0 заданы. Лингвистическое описание таких нечетких чисел имеет вид A = «примерно в интервале [a, b]». Для таких нечетких чисел множества уровня равны

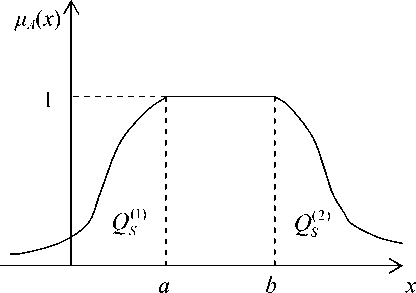
Рис. 5. Геометрическая интерпретация

A ( α ) = [ a + εψ ( α ), b - δψ ( α ) ] , ψ ( α ) = - ln α .

Из формул (12) и (14) получим, что t _∗ = -∞ .

Рассмотрим случай, когда λ = 0 . Тогда неравенства (10) и (16) примут вид:

a_i + b_i ≥ a_j + b_j , ε _i - δ _i ≤ ε _j - δ _j .

Дадим геометрическую интерпретацию (см. рис. 4). Условие a_i + b_i → max означает, что для ЛПР предпочтительнее то число, у которого середина отрезка больше.

Выясним смысл условия ε _i - δ _i ≤ ε _j - δ _j . Для этого вычислим площадь Q_S ⁽¹⁾ (см. рис. 5). Используя формулу для значения интеграла Лапласа [8, с. 248], получим

• a.    ( (v - „v к

  0 π

  S j exP ( - t 2 ) dt =      ^£ S .

  
  

Q S1 = j exp — dx = £

• -^ к    £S7

Аналогично,

+∞             2

Q S ²⁾ = j exp - ^X 2   dx = 5s j exp ( - t ² ) dt = -^3s .

b к    5s   7        0

Поэтому εi -δi ≤εj -δj ⇔ Qi(2) - Qi(1) ≤ Q(j2) -Q(j1) . Таким образом, если середины отрезков, являющиеся ядрами нечетких чисел, совпадают, то предпочтительней из них в сильном смысле будет то, у которого разность QS(2) - QS(1) больше.