Об одном практическом способе решения транспортной задачи с экологическим критерием
Автор: Ассаул Виктор Николаевич, Погодин Игорь Евгеньевич
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 3, 2022 года.
Бесплатный доступ
Рассмотрен алгоритм решения транспортных задач с так называемым экологическим критерием, когда транспортные расходы состоят из тарифной части, пропорциональной количеству перевозимого груза, а также из не зависящих от этого постоянных «штрафных» добавок. Исходя из априорных интегральных оценок соотношения между оценками этих двух частей транспортных расходов предлагается предварительно оценить количественную роль «штрафной» компоненты и степень необходимости строить специальный план с ее учетом. Если учет этой компоненты существенен, то предлагается получить цепочку последовательных решений классических транспортных задач с перестраиваемыми ценами до момента ее зацикливания (повторения). После этого остается выбрать наилучший план, который либо оказывается оптимальным, либо близок к нему и может быть получен за несколько шагов, например, распределительным методом. Исследовано применение этой процедуры при изменении ряда параметров транспортной задачи: относительной доли интегрального вклада штрафов, структуры таблицы штрафов, а также мощностей и емкостей.
Целевая функция, стоимость перевозки, оптимальный план, корректирующий цикл
Короткий адрес: https://sciup.org/148325657
IDR: 148325657 | УДК: 519.86 | DOI: 10.18101/2304-5728-2022-3-3-13
Текст научной статьи Об одном практическом способе решения транспортной задачи с экологическим критерием
Рассмотрим некоторые возможности практического решения транспортной задачи (ТЗ) с «экологическим критерием» [1] (в других формулировках это «ТЗ с фиксированными доплатами», «неоднородная ТЗ» и т. д.). Суть задачи заключается в том, что помимо «сдельной» (тарифной) составляющей, пропорциональной тарифам за каждую единицу перевозимого груза [2], требуется также оплатить некий «штраф» только за сам факт использования конкретного участка трассы независимо от объема перевозки. Эта задача вызывает интерес в течение многих десятиле-тий 1 [3–11]. Однако известны лишь приближенные и часто достаточно сложные способы решения, причем некоторые из них по своим объемам сравнимы с прямым перебором всех вариантов планов, из-за чего они порой представляют чисто академический интерес.
Основная часть
В целях решения таких задач на практике для начала предлагается оценить, насколько существенно введение «штрафов» в конкретной задаче может повлиять на ее решение в виде обычной ТЗ только с транспортными «тарифной» ( C ) и без «штрафной» ( D ) составляющих по всей таблице (рассматривать эти вклады для каких-то отдельных частей таблицы не имеет смысла, поскольку оптимальные планы задачи не найдены и могут касаться различных частей таблицы). Введем следующий интегральный показатель:
_ E n = i Е m = 1 ^ min4, B )
-Rn = .
0 nm
Ew E j = i d i,j
Здесь Ai , i =1÷ n — мощности поставщиков;
B j , j =1÷ m — емкости потребителей.
Целесообразно также использовать отношения характеристик «тарифной» и «штрафной» составляющих по каждой клетке таблицы:
ci j *min( Ai , Bj )
R. . = —,-------------и оперировать их средними значениями:
-
i , j di , j
R
i , j
n mR
Z—ii = 1 Z—ij = 1 i , j
n * m
и среднеквадратичными отклонениями (СКО):
2 0,5
EnE^Ry-R^
по всем клеткам таблицы.
n * m
Если эти интегральные (средние) характеристики существенно больше единицы, т. е. «штрафная» составляющая относительно невелика, то можно решать классическую ТЗ, задав только несколько измененные (модифицированные) тарифы:
dij cmi j = ci j +----,—r.
Можно использовать оптимальный план классической ТЗ также и в случае, если СКО «штрафной» компоненты существенно меньше, чем СКО «тарифной» компоненты.
В противном случае влияние «штрафной» составляющей значительно и должно учитываться иным образом при выборе оптимального плана. Начав с решения ТЗ с теми же измененными тарифами, далее будем (мно- гократно) повторять такие классические решения ТЗ, каждый раз пере- считывая модифицированные тарифы по правилу:
c
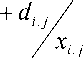
i, J где xij — перевозка, назначенная в последнем плане в ячейку с адресом (i, J) [1].
Эта процедура относится к ячейкам транспортной таблицы оптимального плана. Исследуем применение этой процедуры, изменяя в задачах: а) относительную долю интегрального вклада штрафов;
-
б) размер таблиц;
-
в) структуру таблицы штрафов;
-
г) структуру партнеров, их емкости и мощности.
В качестве первого примера рассмотрим следующую транспортную задачу (табл. 1):
Таблица 1
|
Ai\Bj |
9 |
18 |
23 |
|||
|
16 |
9 |
20 |
4 |
45 |
7 |
29 |
|
22 |
5 |
39 |
3 |
50 |
6 |
36 |
|
12 |
1 |
60 |
8 |
22 |
2 |
54 |
На примере тарифов, заданных в левых верхних углах ячеек, и исходных штрафов (в правых нижних углах ячеек табл.1) с различными значениями пробного коэффициента к по правилу:
cm j
d
= С +Tjv min (AiBj)
строились условные модифицированные тарифы cmi , j , для которых делались оценки параметров сравнения Ro и Ri,j , а также находились начальные оптимальные планы для классической ТЗ с оценкой соответствующей тарифной составляющей.
В таблице 2 пошагово представлена процедура получения цикла новых планов на основании пересчета модифицированных тарифов при k = 1. Планы первого и третьего шагов совпадают, что позволяет остановить процесс, выбрав в качестве наилучшего результат второго шага. Наряду с этим в таблице 2 в скобках представлены оптимальный план и полная стоимость перевозок (412).
Таблица 2
|
k |
1 |
|||
|
R o |
1.738 |
|||
|
R |
2.244±1.607 |
|||
|
в в |
Ai\Bj |
9 |
18 |
23 |
|
16 |
11.222 |
6.813 15 |
8.813 1 |
|
|
22 |
9.333 |
5.778 2 |
7.636 20 |
|
|
12 |
7.667 9 |
9.833 |
6.5 3 |
|
|
C o +D o |
205+255=450 |
|||
|
В в св В в |
16 |
11.222 (5) |
6.813 16 |
8.813 (11) |
|
22 |
9.333 (4) |
28 (18) |
7.8 22 |
|
|
12 |
7.667 9 |
9.833 |
6.5 3 (12) |
|
|
C o +D o |
232+192=424 (412) |
|||
|
в св В в |
16 |
1.222 |
7 16 |
36 |
|
22 |
9.333 |
5.778 2 |
7.636 20 |
|
|
12 |
7.667 9 |
15.333 |
6.5 3 |
|
|
C o +D o |
205+255=450 |
|||
С целью иллюстрации влияния амплитудного фактора доли штрафной компоненты при неизменной структуре таблицы штрафов в табл. 3 представлены аналогичные цепочки расчетов для k =25, 0.5, 0.25 по столбцам.
Таблица 3
|
k |
25 |
0.5 |
0.25 |
|||||||
|
R o |
43.5 |
0.9 |
0.4 |
|||||||
|
R |
56.1±40.1 |
1.1±0.8 |
0.6±0.4 |
|||||||
|
в |
Ai\Bj |
9 |
18 |
23 |
9 |
18 |
23 |
9 |
18 |
23 |
|
16 |
16 |
9 |
7 |
9 |
6 |
1 |
||||
|
22 |
2 |
20 |
11 |
11 |
22 |
|||||
|
12 |
9 |
3 |
12 |
12 |
||||||
|
C o +D o |
205+10=215 |
232+410=642 |
340+608=948 |
|||||||
|
в св В в |
16 |
16 |
16 |
9 |
7 |
|||||
|
22 |
2 |
20 |
9 |
13 |
2 |
|||||
|
12 |
9 |
3 |
5 |
7 |
11 |
1 |
||||
|
C o +D o |
205+10=215 |
250+388=638 |
331+708=1039 |
|||||||
|
cd в в |
16 |
16 |
16 |
9 |
7 |
|||||
|
22 |
2 |
20 |
22 |
6 |
16 |
|||||
|
12 |
9 |
3 |
9 |
2 |
1 |
12 |
||||
|
C o +D o |
205+10=215 |
223+434=657 |
340+628=968 |
|||||||
|
в св В в |
16 |
15 |
1 |
9 |
7 |
|||||
|
22 |
22 |
2 |
||||||||
|
12 |
9 |
3 |
11 |
1 |
||||||
|
C o +D o |
232+384=616 |
331+708=1039 |
||||||||
|
cd в в |
16 |
9 |
7 |
|||||||
|
22 |
11 |
11 |
||||||||
|
12 |
12 |
|||||||||
|
C o +D o |
232+410=642 |
|||||||||
Здесь предполагается, что классическая ТЗ с критерием цен легко решается с помощью стандартной процедуры, например, методом «потенциалов». Можно использовать также и другие способы, например, стандартную процедуру « minimize » пакета Mathcad [12].
Как и следовало ожидать, параметры сравнения составляющих C/D Ro и Ri,j имеют тот же порядок, что и задаваемый амплитудный фактор k , отличаясь примерно в 2–3 раза, а найденные таким способом планы перевозок существенно изменяются. При этом увеличивается тарифная составляющая C , которая перестает быть доминирующей при выборе оптимального плана.
Таким образом, по крайней мере, в последних двух случаях ( k ≥ 2; R o ≤ 0.9; R ≤ 1.1±0.8) требуется по-новому проводить процедуру поиска наилучших планов.
Анализируя результаты представленных в столбиках трех ТЗ с различными значениями k , можно заметить, что в каждой из них наблюдаются цепочки циклических повторений ситуаций различной длины, на которых можно найти наилучший план перевозок, наиболее близкий к оптимальному.
Аналогично в таблице 4 рассмотрена такая же задача большей размерности (4*4) , а в скобках представлен оптимальный план с полной стоимостью перевозок 1636.
Таблица 4
|
Ai\Bj |
28 |
20 |
12 |
20 |
|
15 |
9 120 |
24 3 (3) 20 |
16 12 (12) 50 |
18 40 |
|
22 |
17 10 (2) 40 |
8 120 |
19 30 |
14 12 (20) 60 |
|
25 |
15 (8) 60 |
12 17 (17) 80 |
21 20 |
13 8 70 |
|
18 |
11 18 (18) 90 |
15 60 |
17 40 |
10 100 |
Анализ полученных решений показывает, что при k ≤ 0.05 влияние штрафной компоненты можно не учитывать. При изменении значений k предложенная процедура приводит к появлению циклов повторяющихся ситуаций различной длины, из которых можно выделить наилучший план с минимальной полной стоимостью перевозок ( C o +D o); длина этих циклов не обнаруживает регулярной связи с априорным соотношением тарифной и штрафной компонент C/D (параметр k ).
Количество используемых шагов при этом несравнимо меньше, чем потребовалось бы при прямом переборе всех планов перевозок. Например, при R o = 2.15; R = 3.21±2.3 до появления повторяющейся ситуации, позволяющей остановить вычислительную процедуру (выделена жирным шрифтом во второй строке табл. 5), требуется сделать 12 шагов. Для этого случая по причине громоздкости полного аналога таблиц 2, 3 в таблице 5 для каждого из этих шагов приведены лишь расчеты двух компонент: C o и D o и полные значения расходов на перевозку S Σ без указания самих промежуточных планов ( C o /D o = 1108/670 = 1.65). Оптимальный план указан жирным курсивом в табл. 5. В то же время при R o= 1075 и R = 1607±1149 требуется только 4 шага и окончательное соотношение C o /D o = 1171/1100 = 1.06.
Таблица 5
|
C o |
D o |
C o +D o |
|
977 |
830 |
1807 |
|
1108 |
670 |
1778 |
|
1112 |
790 |
1902 |
|
941 |
870 |
1811 |
|
1111 |
830 |
1941 |
|
1256 |
550 |
1806 |
|
944 |
990 |
1934 |
|
1027 |
830 |
1857 |
|
1813 |
710 |
2023 |
|
1087 |
710 |
1797 |
|
1034 |
1010 |
2044 |
|
1087 |
710 |
1797 |
Наконец, в таблице 6 представлено получение циклических процедур для двух различных структур таблицы штрафов при общей таблице тарифов. Наилучший план со штрафами, представленными выше дроби, совпадает с оптимальным, в то время как наилучший план со штрафами ниже дроби отличается от оптимального под дробью в скобках и дающего общую стоимость 679.
Таблица 6
|
Ai\Bj |
19 |
5 |
12 |
11 |
|
16 |
8 11/16 /(16) 30/59 |
5 5/ 40/63 |
10 50/74 |
9 25/129 |
|
10 |
6 1/ 34/70 |
11 30/22 |
7 60/61 |
5 9/10( 10 ) 48/38 |
|
14 |
12 /1 58/70 |
13 /( 1 ) 38/31 |
9 12/12 ( 12 ) 62/55 |
10 2/1( 1 ) 51/63 |
|
7 |
7 7/2( 3 ) 45/49 |
6 /5( 4 ) 53/23 |
14 30/34 |
9 55/73 |
Для первого варианта системы штрафов (фактор априорного отношения компонент C/D : R o=1.40 ( R =1.86±1.53)) задача решается за три шага (левая половина табл. 7):
Таблица 7
|
C o |
D o |
C o +D o |
C o |
D o |
C o +Do |
|
341 |
310 |
651 |
352 |
357 |
709 |
|
345 |
308 |
653 |
369 |
349 |
718 |
|
341 |
310 |
651 |
352 |
357 |
709 |
Если полностью изменить матрицу штрафов (их значения представлены в табл. 6 через дробь в правых нижних углах ячеек), сохранив на прежнем уровне фактор C/D : R o = 1.42 ( R = 3.2±2.3), то задача решается также за три шага с наилучшим планом, получаемым на первом шаге (правая половина табл. 7).
Два варианта задачи, различающиеся только структурой мощностей производителей и емкостей заказчиков, дают совершенно различные планы, причем оба на первом шаге процедуры с цепочкой из трех шагов (левая ( R o= 1.64; R = 1.76±1.04) и правая ( R o= 2.08; R = 2.16±0.99) половины табл. 8).
Таблица 8
|
Ai\Bj |
19 |
5 |
12 |
11 |
Ai\Bj |
8 |
20 |
11 |
16 |
|
16 |
6 16 39 |
8 40 |
9 39 |
10 68 |
12 |
6 8 (8) 39 |
8 2(4) 40 |
9 2 39 |
10 68 |
|
10 |
8 30 |
7 33 |
6 6 38 |
7 4 50 |
10 |
8 30 |
7 33 |
6 9(9) 38 |
7 1(1) 50 |
|
14 |
6 3 33 |
5 5 45 |
10 6 25 |
9 60 |
18 |
6 33 |
5 18(1 6) 45 |
10 (2) 25 |
9 60 |
|
7 |
5 38 |
9 30 |
8 35 |
5 7 66 |
15 |
5 38 |
9 30 |
8 35 |
5 15(15) 66 |
С o +D o = 298+296 =594 С o +D o = 308+317 = 625
Здесь также наилучший план задачи в левой части таблицы 8 совпадает с оптимальным, в то время как наилучший план задачи в правой части отличается от оптимального, представленного в скобках и дающего общую стоимость перевозок 613 .
Следует отметить, что по девяти рассмотренным задачам отношение «штрафной» части к «тарифной» С o /D o тесно коррелирует ( r ≥0.9) с аналогичным отношением интегральных частей из априорных расчетов С/D : ln [ С o /D o]=0.8* ln [( С/D )]-0.3. Это указывает на уменьшение относительной доли тарифной части расходов в наилучших найденных планах D o по сравнению с априорными интегральными оценками, поскольку некоторые участки выгоднее использовать с их неполной загрузкой
( xLj < min ( A , j
Такая связь может позволить найти оценки отношения этих составляющих еще до получения самих планов решения задачи.
Заключение
Таким образом, предложенный путь решения транспортной задачи с экологическим критерием, носящий до некоторой степени эвристический характер, заключается в следующем:
Исходя из простых априорных интегральных оценок отношения «штрафной» части к «тарифной», если оно составляет более нескольких процентов (например, около 5% для задач (3*3) и 1% для задач (4*4)), то предлагается получить цепочку последовательных решений для планов классических транспортных задач с измененными тарифами (ценами) до момента зацикливания (повторения ситуаций), после чего следует выбрать среди них наилучший план и при необходимости уточнить его, например, распределительным методом.
Список литературы Об одном практическом способе решения транспортной задачи с экологическим критерием
- Ассаул В. Н., Погодин И. Е. О транспортной задаче с экологическим критерием // Экономика и математические методы. 2019. Т. 55, № 2. С. 58-64. Текст: непосредственный.
- Канторович Л. В. О перемещении масс // Доклады Академии наук СССР. 1942. Т. 37. С. 227-229. Текст: непосредственный.
- Бирман И. Я. Оптимальное программирование. Москва: Экономика, 1968. 231 с. Текст: непосредственный.
- Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирование. Москва: Наука, 1969. 368 с. Текст: непосредственный.
- Поляк Р. А. Об одной неоднородной транспортной задаче // Математические модели и методы оптимального планирования: сборник статей. Новосибирск: Наука, 1966. С. 109-115. Текст: непосредственный.
- Седова С. В., Лебедев С. С. Решение одной задачи размещения с использованием узловых векторов разрешающих множителей // Экономика и математические методы. 1999. Т. 35, № 3. С. 116-121. Текст: непосредственный.
- Седова С. В., Лебедев С. С. Метод узловых векторов целочисленного программирования. 2. Задачи специального вида: препринт ЦЭМИ. WP/2000/094. 2001. 88 с. Текст: непосредственный.
- Сигал И. Х., Иванова А. П. Введение в прикладное и дискретное программирование: модели и вычислительные алгоритмы. Москва: Физматлит, 2007. С. 45-49. Текст: непосредственный.
- Фролькис В. А. Введение в теорию и методы оптимизации для экономистов. Санкт-Петербург: Питер, 2002. 320 с. Текст: непосредственный.
- Хоанг Туй. Вогнутое программирование при линейных ограничениях // Доклады Академии наук СССР. 1964. Т. 159, № 1. С. 32-35. Текст: непосредственный.
- Balinski M. L. Fixed Cost Transportation Problem // Naval Res. Log. Quart. 1961. Vol. 8, N. 1. P. 41-54.
- Кирьянов Д. В. Mathcad 12 в подлиннике. Санкт-Петербург: БХВ-Петербург, 2005. 557 с. С. 192-193. Текст: непосредственный.


