Об одном представлении аналитических функций
Бесплатный доступ
Основываясь на полученных ранее оценках для G -функций и 0-нормированных систем функций относительно оператора Лапласа, найдено новое разложение аналитических функций в обобщенную формулу Альманси.
Короткий адрес: https://sciup.org/147158542
IDR: 147158542 | УДК: 517.956.22
Текст научной статьи Об одном представлении аналитических функций
Рассмотрим полиномы следующего вида [3]
[i/2] I т |2< *-2г,!
Ga(xm) = У (-1)' «----- (1)
-
12,2) ;(»-l + 25,2)z
где (a,b)k = a(a + b)...(a + kb-b') - обобщенный символ Похгаммера, причем (а,6)0 = 1, tw' - факториальная степень tm' =tm/m\, а [а] - целая часть числа a . Полиномы Gk^x^ вида (1) называются G -полиномами степени к , порядка 5 и рода п . В [7] установлено, что произведение однородного гармонического полинома от п-1 переменных Н^х^.у^ на G -полином Gk(xw) дает гармонический полином от п переменных и(х) = Gk(xw)Hs(x^n_^) . Более того, всякий гармонический полином от и переменных может быть разложен в сумму полиномов такого вида.
Такой подход к построению гармонических полиномов позволяет получать гармонические полиномы в виде произведения различных G -полиномов где v е Ng , vx>"->vn и vn = 0,1. При рассмотрении следов G -полиномов на единичной сфере возникает понятие G -функции. Следующая функция
[(&—s)/2] Jc-s-2i'м f2xi*s/2
GsAt) = У (-1) ----——---
Й (2,2)z(«-l + 2s,2)z называется G -функцией степени к , порядка s и рода п.
Верны следующие утверждения:
Лемма 1. [4] Пусть функция / еС(о$п) задана в виде /(х) = ф(\х\,хп)Рк(х), где Рк(х) однородный гармонический полином степени к от переменной х = (хх,.„,хп-х) и ф^ C(5Sn), тогда
Li = дW где соп =| dSn | - площадь единичной сферы в R" .
Теорема 1. [3] Нормированная в Z2(-l,l) с весом /?„(/) = (1-/2Уп~3)/2 G -функция Gk"^ удовлетворяет оценке
| ОкЧО 1^24^ + (и-2)/2)2п"3, к > s, п > 2.
Основываясь на свойствах гармонических полиномов GAX), в теореме 2, известное утверждение Альманси [1]: «для любого полинома Р(х) существуют гармонические полиномы Н0(х),.„, Нк(х) такие, что
РА = Яо (х)+1 х |2 Нх (х) + ■ • ■ +1 х |2* Нк (х),» (3)
распространяется на аналитические функции действительного переменного xeRn . Затем, в теоремах 3 и 4, этот результат уточняется - даются формулы нахождения полиномов Нк{х) и функ- ций ик(х) = НДх), когда Р(х) не полином. Теорема 4 проиллюстрирована на представлении решений уравнения Гельмгольца через гармонические функции (25).
Следует заметить, что в [2] (теорема 2.2) формула Альманси была уже распространена на голоморфные функции. Оказалось, что полученная ниже формула (18) несколько отличается от формулы (2.9), найденной в [2]. Обобщения другого рода были получены в 1958 г. М. Николеску [8], где найдено разложение Альманси для класса операторов от двух переменных, который включает в себя и оператор теплопроводности. В работе [9] рассматривалось разложение Альманси для решений уравнения □”* и = 0, где о- Ах + Яд2 / dz2 или □= Ах + Яд / 8t при Я е СI {0}.
Полигармонические функции
Имеет место следующее свойство гармонических полиномов (^(х) (2).
Лемма 2. Для нормированного в ДЦ5Д гармонического полинома G G^ =1X Г1 П G^+b”-'+1(cos^_,+1), м где G -функция Ок’ЧО нормированная в Z2(~M) свесом /9и0) = (1-Z2y”~3)/2. На основании данной леммы нетрудно доказать Теорема 2. Для любой функции /(х), аналитической в начале координат, существуют гармонические функции и0(х),...,ии(х),..., определенные в некоторой окрестности начала координат D такие, что № = ^\х\21 и^х), xeD. (4) 1=0 Замечание 1. Доказательство теоремы не является конструктивным так же как и формула Альманси. Оно опирается лишь на оценку теоремы 1 и не позволяет строить гармонические функции и^ по известной функции /(х). Формулу для нахождения гармонических функций м;(х) дает теорема 4. Рассмотрим область DcRn, обладающую свойством звездности Vx е D, Vz е [0,1] txeD и определим на ней следующую последовательность функций: м(х), к = 0 Gk (х; и) = * 4* к'. J (Аг-1)! к>0, где и(х) некоторая гармоническая в D функция. Система функций {ОДх;м)| & = 0,1,...} является 0-нормированной относительно оператора А в D [5], т.е. в области D верны равенства АС4(х;и) = С4_](х;и) и AGo(x;u) = O. Лемма 3. Для всякой полигармонической функции Р(х) существуют такие гармонические функции v0(x),...,vm(x), что имеет место равенство Р(х) = Go (х; v0) + Gt (х; ^) + ... + Gm (х; vm). Доказательство. Рассмотрим полигармоническую функцию Р(х) порядка т т.е. такую функцию, что Ре С®ЦУ) и Ат/’(х) = 0. Согласно формуле Альманси (3), найдутся такие гармонические функции иДх), что т РЦ>^>\2к икЦ\ 4=0 Из определения функции GA(x;v) видно, что ее можно представить в виде произведения некоторой гармонической функции на полином | х |2*. Записывая функцию ик (х) из (6), при к > 1, в виде ик(х) = —т— ————an/2 xvk(ax)da, (7) 4^!» (А:-1)! А формулу (6) можно записать в форме (5). Покажем, что уравнение (7) можно однозначно разрешить относительно vk(x), причем функция vk(x) получается при этом гармонической. Это и до кажет утверждение леммы. Введем следующий оператор Л = Vx —. При qeN и s > 0, верно равенство м (Л + 5 +1) f ——^—asv(ax)da = £ ————as+iv(ax)da,(8) Л (9-1)! а также при q = О (Л + я-1) asv(ax) da = v(x).(9) Пусть к = 1. В силу равенства (9) взятого при s = и/2 -1 получим 4^A + ^U](x) = ^A + ^ ^all/2"~1vx(ax)da = vx(x).(10) Пусть к > 1. Тогда, в силу равенства (8) взятого при s = л/2 -1 получим ^!4* Л + — ^(х)^ I--------a 2vk(ax)da. \ 2) (к-2)1 Используя опять (8), но уже при х = п/2 найдем А14* Л + — Л + —+ 1 ul(x)= [ ----—a 2 Sk(ax)da. у 2 Д 2 ) (£-3)! Продолжая указанный процесс, найдем к-2 / \, £!4 «t(x)= Га^к 2vk(ax)da. i=o V 2> Воспользовавшись равенством (9) при s = n/2 + k-2 и внося множитель кАк под знак произведения, будем иметь vkW = П 4(z' + i=0 к 22 В силу (10) данное равенство верно и при к = 1. Итак, функция гДх) найдена. Для окончательного доказательства леммы следует заметить, что оператор Л переводит гармонические функции в гармонические. □ Таким образом, в силу леммы 3, для произвольной полигармонической функции Р(х) имеет место равенство Р(х) = Go (х; v0 ) + Gx (х; ^) + ... + Gm (х; vm) (И) где vk(x) - неизвестные гармонические функции. Найдем зависимость этих функций от функции Р(х). В силу О-нормированности системы функций {СЛ(х;и)| к = 0,1,...} относительно оператора А в области D верно равенство ^_г(х;у(х)), к>г к = г. к<г Отсюда нетрудно получить, что \mP^x) = \mGMvQ)^^Gx(x-vx)A-..^^mGm^m) = Далее, Am"1P(x) = Go (х; vm_x) + G] (х; vm ) = vm_x (х) +an,2-xvm (ах) da и значит, используя предыдущее равенство, запишем vm4 (х) = АтЧР(х) - ™- an/24 АтР(ах) da. (12) Докажем следующую формулу для вычисления функции vm_,(x): (1Э) 4 s! Л (s —1)! где z = 1,.,.,/и . При z = 1 она имеет вид (12). Предполагая верность (13) при некотором j > 1 и для всех / < у, докажем ее справедливость и при z = у +1. Из (11) нетрудно получить откуда ^4 z! 0-1)! J Используя предположение индукции (13) и равенство ^Р = 0 для к > т найдем ^4' zl » 0-1)! 4" s! ( х t ^n/2-1 ^^Г PS"X^HWSp( Обозначим последнее слагаемое в полученной сумме через 7(х). Тогда СО | |2/ , /-1 1=2 4 5=1 где обозначено хл = (1-^ у (-1/^-’ + ы£1 у W П SO-^(s-l)! 0-1)! S0-5)W Вычисления показывают, что J^= ^^)Г [(-/?)W -1] и значит . х' (-1/ И2/ а^О-а/-1„/2-i ,т- ,-i+s Й 4^ s! Ь (.-1)! (15) г 4s s! -b (5-1)! k 5 Подставляя вычисленное значение I(x) - последнего слагаемого в (14), будем иметь =5”-^-|P(x)+f;fcEiy. ^У<ЦйТа-'г-|Д-^1"Р(а,)5а, v 45 SJ Д) (5-1)! что совпадает с формулой (13) при z = У +1. Индукция доказана. Таким образом, основываясь на (13), мы имеем для vk(x) общее выражение vk(x) = ^кР(х) + f .у.......a^^PkaxW, (16) 4 5! (5-1)! где к = 0,...,т . Таким образом, доказана теорема, уточняющая лемму 3. □ Теорема 3. Для любой полигармонической функции Р(х) имеет место равенство (5) Р(х) = Go (х; v0) + G, (х; ^) + ... + Gm (х; vm), где гармонические функции v0(x),...,vm(x) находятся из равенства (16). Замечание 2. При к = 0 формула (16) принимает вид 5! » («-!)! и задает гармоническую составляющую произвольного полинома Р^ в формуле Альманси P(x)-v0(x)+|x|2Q(x). Заметим, что в [6] получено другое - «дифференциальное» представление гармонического полинома v0(x). Докажем теперь, что для аналитической в начале координат функции Дх) имеет место формула (5) с бесконечным значением параметра т т.е. № = v0(x) + ^ { (jl _1), an,24vk(ax)da, x&D. (17) Теорема 4. Для любой функции /(х) аналитической в начале координат имеет место равенство (17), в котором гармонические функции v0(x),...,v„(x),... определены в некоторой звездной области D с центром в начале координат и задаются формулой = л‘/М + ^(J 1 t( , * “ a^-'^-f^da. (18) й 4 si * (s-l)l Замечание 3. Формула (18) несколько отличается от аналогичной формулы (2.9), полученной ранее в [2]. Доказательство. Покажем сначала, что функции ^(х), найденные из равенства (18) являются гармоническими (этого не требовалось при доказательстве теоремы 3, поскольку там мы исходили из леммы 3) и при подстановке в (17) обращают его в тождество. Применим оператор А к обеим частям равенства (18), считая законным дифференцирование под знаком суммирования. Если использовать равенство A ^J х j2s м(х)] = 4з|х|25"2^A + s + -^--1^m(x)+|x|2s Au(x), а также формулы (8) и (9), то можно убедиться, что Avt(x) = 0. Докажем теперь, что имеет место формула (17), где гДх) находятся из (18). Для этого под ставим vA(x) в (17). Получим № = /(x) + £> / 1 L ■ ...--a a Kax^da + 4J s! » (д-1)! +У 1 M_ (0-“) a^-'^Kax-jdax У Й4* t! *> (»-D! ” ’ Д (-1/ (x]2^ 4^5k\s\ ^'"t-“Г г ^'Г Обозначим последнюю сумму в полученном выражении через /Дх). Тогда А« = 2 k, s=l (-1/|х|^ 4*+i £!s! У-«У xa2s+nl2 1 (И)! Имеет место равенство /Дх) = -/(х) при /(х) = Дт 7 ’/Дх). Поэтому, в соответствии с (15) А00 = -£ 5=1 (-1/1^ I2' 4s s! а5 1(1-«У 1n/2-iA5zz х, --—а ' Д f(ax)da- Г —ап'2 xAs/(ax)da. ■Ь (з-1)! После подстановки полученного значения /Дх) в (19) получим тождество /(х) = /(х). Для окончательного доказательства теоремы необходимо обосновать правомерность проделанных выше действий, т.е. доказать что: 1) ряды в (18) VZ равномерно сходятся по х в некоторой звездной области D и их можно почленно дифференцировать в D, а значит их суммы гармонические в D функции (лемма 5 и следствие из нее); 2) если функции гДх) определены в D и находятся из (18), то ряд (17) равномерно сходится в некоторой подобласти D' с D и его можно почленно дифференцировать в D' (лемма 6). Леммы 4-6, приведенные ниже, решают эти задачи. Поэтому, теорему 4, можно считать доказанной. □ Лемма 4. Пусть L(D) = L(D ,...,DXn) дифференциальный оператор с постоянными коэффициентами и функция /(х) аналитическая в точке х(°) е Rn, тогда существуют такие положительные числа С и £, что для х таких, что | х-х^ |< £ имеет место оценка где фр) = С dps -1) и многочлен Z(^) получен из многочлена Z(^) заменой его коэффициентов аа на их модули | аа |. Доказательство. Из условия леммы, функция /(х) аналитическая в точке х^ е Rn, а поэтому /(х) = "^^ fa(x-х0)“, причем ряд абсолютно сходится в D - некоторой окрестности точки х<°\ Отсюда следует, что существует f >0 такое, что (x^+f.—.x^+^eZ) и значит, для всех к, имеет место неравенство |о1=4 из которого, с учетом сделанных выше обозначений и неравенства | х,--xf |<| х-х(0^ |, следует оценка l/WI^Z Z l/all^-^rl^S 4=0 |а|=4 4=0 V ОО ^Zi/jscZ У |а[=4 4=0 Л (0)|У | X - Х^ J = <р(\х-х№ |), справедливая для | х - х(°) |< £. Теперь оценим производную D^f{x) от функции /(х) порядка Д = (Д,...,Д„). Для этого рассмотрим множитель Са>р =а\/(а- Р)\ при а > Д (а > Д о di,а, > Д\ Докажем, что Сар<---. (22) Применим индукцию по размерности и. При и = 1 эта формула, очевидно, верна и в ней имеет место равенство. Пусть формула (22) верна при и = и-1. Обозначим через а е Z"”1 вектор, полученный из вектора а отбрасыванием его первой компоненты. Тогда = «, («,-XYA«x-Р ^С^р <|а|(|а|-1)...(|а|-Д ^С5р для а> Д. Поэтому, в силу предположения индукции и неравенства | а |=| а | -ах <| а | - Д, полу чим <\а\(\ос\-\уД\ос\-рх +1) Са,д (И-ДУ 1«П (И~Д-|11)! (1«ЫД1)!' На основании (22) при / =|х-х(°) | получим \прАху< ycap\fa kx-x^f-^^ У — аг^Д 4=|Д| VK I Р U- 4=|Д| (к-1Р№ = С У £-kD\P4k = D\^ = Dfcpm , (0)| 1 1 X-tie 1 для | х - х^0-11< е . Отсюда сразу следует, что IЦОХх,...,ОХп|< YI^ II Da№IS£1aa I^^(О^и, = ^.„Ж^. a a Что и требовалось доказать. □ Лемма 5. Пусть функция /(х) аналитическая в некоторой звездной области D, тогда ряд №/) Ч J «nQ-X^SK«xW, (20) 4s 5! « (5-1)! равномерно сходится по х в некоторой звездной подобласти Д' с D и возможно дифференцирование под знаком суммы. Доказательство. Воспользуемся леммой 4 в частном случае L(D) = AJ и х^ = 0 . Легко видеть, что в этом случае L(Dt,...,Dt)~ L{Dt,...,Dt) = nsDjs, а поэтому, существуют такие положительные С и £, что для | х |< Е \\s№\ где как и выше ф^ = СеКе -1) . Отсюда, учитывая что а е [0,1], получим |д7(«х)|<й^27(^^ Применяя полученное неравенство в формуле (23), найдем | /) |< ^(| х |) + - У .. J25 Л1)’ (IX I) da. 1 J ' 2 ^ 2s! !2(s -1)!! "V (25-1)! ' 1 м Для интегрального члена, при п > 2 и | х |< г имеем оценку . A I |2$ j (1 -аГХаИп,И ^ДЛ-^ф^ \x^da< (25-1)! ^ D^^^dt < Ф^$ °(И). Отсюда находим (25-1)! (V^lxl)2-1м 25!!2(5-1)!! (2s-l)! 9 ( \Рф№фф\^^У4 2 5=1 G^W^i (25-1)! Ф9"ХЧ\х\\ или с учетом равенства £/25-1^(25-1)(| 5=1 верного при достаточно малых /, получим -у^((1+7й)|х|)< y-+i ^((i+7«)|x|), где х уже должно быть таким, что |x| Из приведенных выше оценок видно, что ряд DaF(x’,f) сходится равномерно в D' и значит DaF(x;/) = F(x; Da f}. Лемма доказана. □ Следствие 1. Ряд F(x\\mf) сходится равномерно по х в той же области что и ряд F(x;/). Доказательство. Нетрудно видеть, что согласно (22), рассуждения, аналогичные рассуждениям леммы 5, можно применить и к функции А™/. Тогда получим | Р<х-дтл 1^ птФ^тЧ\ х \)+пт ——11----22J Отсюда, поскольку функция ф^ХО^т'-Сб/^Е-^”1*^ удовлетворяет неравенствам Ф^ДХ - 7й) | х |) > 0 и ф^^ -\-х[п') | х |) > ^w)(| х I), аналогично (25), получим | F(x; Ат Л |< (2^/4 + l)nV2m40 + ^ | х |), (26) где х, также как и в (25), такое, что | х |< б/(1 + 2/). □ Лемма 6. Пусть функции ^(х) определяются по формуле (18) и заданы в звездной области D, тогда ряд 00 1 I т |2А Я Л - /у^-1 G(x) сходится равномерно по х в некоторой звездной подобласти D' с. D и позволяет дифференцирование под знаком суммы. Доказательство. Нетрудно видеть, что vk(x) = Р(хДкЛ. Поэтому, согласно следствия 1, все функции vk(x) определены в некоторой D* cD . Более точно, в соответствии с (23), найдутся такие положительные С и £, что V£ | vk(x) |< (ТЙ/4 + Х^ф^Хо + Хп) IXI), где, как и прежде, фЛ = Се/(е -/). Обозначая е* = dXX + 2г) и С = С(4п1% +1), для новой функции ^(/), найдем | vk(x) |< пкф^кХ\ х I) ■ Тогда, | G^ |< ^(| х |) + f 1 <^М1 jj Для функций ф^Л^ S t < s'"), очевидно, имеет место неравенство ф^к\аГ) < ф^Л,гДе «е [0,1] и поэтому И 0—Л—а^^ф^Ха | х \)da< 22А)(1 х |) £ 5_22—a"/2_1da < < ф^кХ х I) —da =—22^(l х |). 1 -Ь (^-1)! kV 1 м Значит, |°(^^ S “?<’(i^) < i 6^г2<21,(| t=0 (2к!к=0 или с учетом равенства /2s,!^)(2$)^ _ £C222i^L2z2 5=0 2 верного при достаточно малых t, получим ф((Х + ^)\х\') + ф((Х-Хп')\х\) 2 ’ где х должно быть таким, что | х|< е7(\ + 4п) = е!{\ + Хп)2 . Аналогично проделанному, можно показать, что ряд, задающий G(x), допускает почленное дифференцирование под знаком суммы, и полученный в результате этого ряд будет сходиться равномерно. Значит, функцию G(x) можно дифференцировать под знаком суммы. Лемма доказана. □ Пример 1. Рассмотрим уравнение Гельмгольца I X I w(x) = v(x) + Л-—— gJ-Za(l-a)l х I2 p(ctx)an/2 xda. и [5] Sm^ ^=0( ^ pg^mg^ • Поскольку, согласно теореме 4, функция v^x) гармоническая в П,тои и(х) гармоническая в Q. Теперь из (17) находим v(x) = «(х)- Z—^~ ^g^^l-oOIxp^ax)^2 xda. Формулы (24) и (25), задающие взаимно однозначное соответствие между гармоническими в О функциями и решениями уравнения Гельмгольца, совпадают с ранее полученными в [5, 10].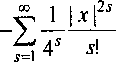
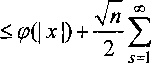
0 и ^((1 + Vh)|x|)>^(|x|). Поэтому, в области D1 = ^х\<е7(1 + ^^ , где s' <е ряд из (23) сходится равномерно по х.
Список литературы Об одном представлении аналитических функций
- Almansi, Е. Sull'integrazione dell'equazione differenziale ∆2nu = 0/Е. Almansi//Ann. Mat. Рига Appl. -1899. -V. 3, № 2. -P. 1-51.
- Aronszajn, N. Polyharmonic functions/N. Aronszajn, M. T. Creese, L. J. Lipkin. -Oxford Univ. Press: New York, 1983. -265 p.
- Karachik, V.V. On some special polynomials/V.V. Karachik//Proceedings of AMS. -2004. V. 132.-P. 1049-1058.
- Karachik, V.V. On one set of orthogonal harmonic polynomials/V.V. Karachik//Proceedings of AMS. -1998. -V. 126, № 12. -P. 3513-3519.
- Karachik, V.V. Normalized system of functions with respect to the Laplace operator and its applications/V.V. Karachik//Journal of Mathematical Analysis and Applications. -2003. -V. 287, №2.-P. 577-592.
- Karachik, V.V. Harmonic polynomials and the divisibility problem/V.V. Karachik//Proceedings of AMS. -1997. -V. 125, №11. -P. 3257-3258.
- Karachik, V.V. Polynomial solutions to the systems of partial differential equations with constant coefficients/V.V. Karachik//Yokohama Mathematical Journal. -2000. -V.47, № 2. -P.121-142.
- Nicolescu, M. Probléme de l'analyticité par rapport á un opérateur linéaire/M. Nicolescu//Stadia Math. -1958. -V. 16. -P. 353-363.
- Ren, G. B. Almansi decompositions for polyharmonic, polyheat, and polywave functions/G.B. Ren, U. Kahler//Stadia Math. -2006. -V.172, № 1. -P. 91-100.
- Векуа, И.Н. Новые методы решения эллиптических уравнений/И.Н. Векуа. -М.-Л.: ОГИЗ, 1948.-296 с.


